+ - 0:00:00
Notes for current slide
Notes for next slide

2.6: Long Run Industry Equilibrium

ECON 306 · Microeconomic Analysis · Fall 2019

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microf19
microF19.classes.ryansafner.com

Firm's Long Run Supply Decisions

Firm Decisions in the Long Run I

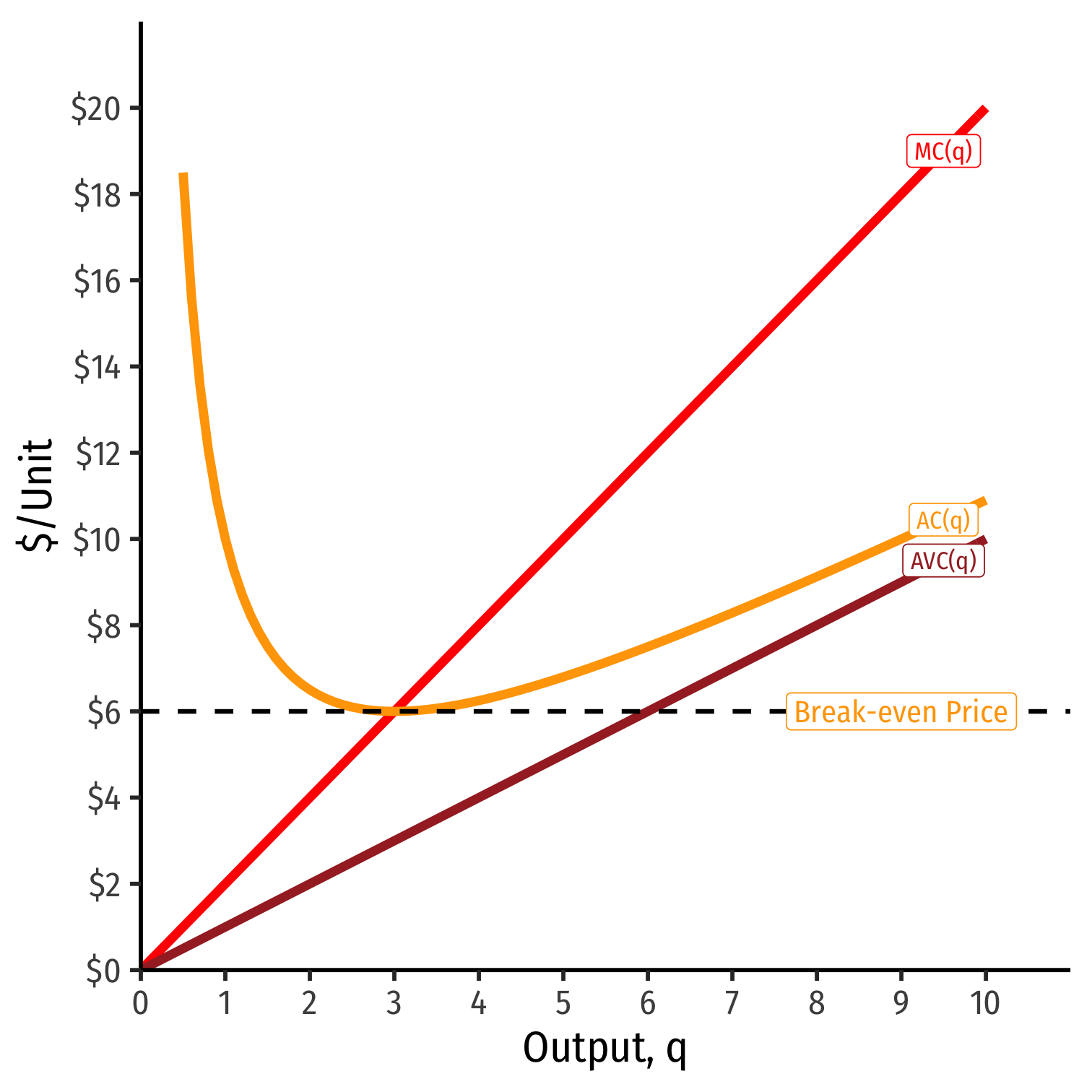
  • AC(q)min happens at a market price of $6.00

  • At $6.00, the firm earns "normal economic profits" of 0.

  • At any market price below $6.00, firm earns losses

    • In the Short Run: firm shuts down production only if p<AVC(q)

  • At any market price above $6.00, firm earns "supernormal profits"

Firm Supply Decisions in the Short Run vs. Long Run

  • Short run: firms that shut down (q∗=0) stuck in market, incur fixed costs π=−f
    • Firms cannot change their fixed factor (capital k)

Firm Supply Decisions in the Short Run vs. Long Run

  • Short run: firms that shut down (q∗=0) stuck in market, incur fixed costs π=−f

    • Firms cannot change their fixed factor (capital k)

  • Long run: firms earning losses (π<0) can exit the market and earn π=0

    • No more fixed costs, firms can sell/abandon f at q∗=0

Firm Supply Decisions in the Short Run vs. Long Run

  • Short run: firms that shut down (q∗=0) stuck in market, incur fixed costs π=−f

    • Firms cannot change their fixed factor (capital k)

  • Long run: firms earning losses (π<0) can exit the market and earn π=0

    • No more fixed costs, firms can sell/abandon f at q∗=0

  • Entrepreneurs & Firms not currently in market can choose to enter and start producing, if entry would earn them π>0

Firm's Long Run Supply: Visualizing

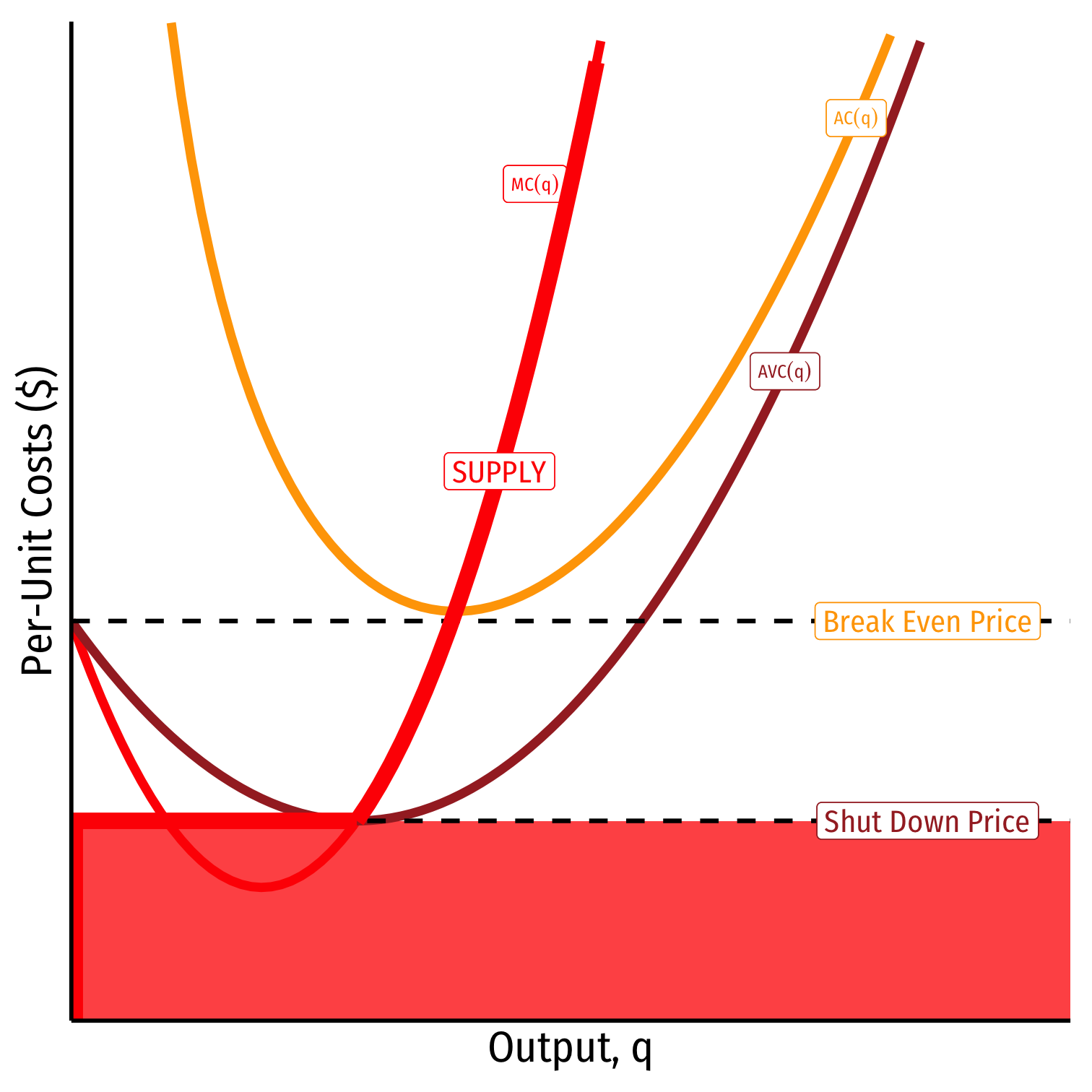
When p<AVC

  • Profits are negative

  • Short run: shut down production

    • Firm loses more π by producing than by not producing

  • Long run: firms in industry exit the industry

    • No new firms will enter this industry

Firm's Long Run Supply: Visualizing

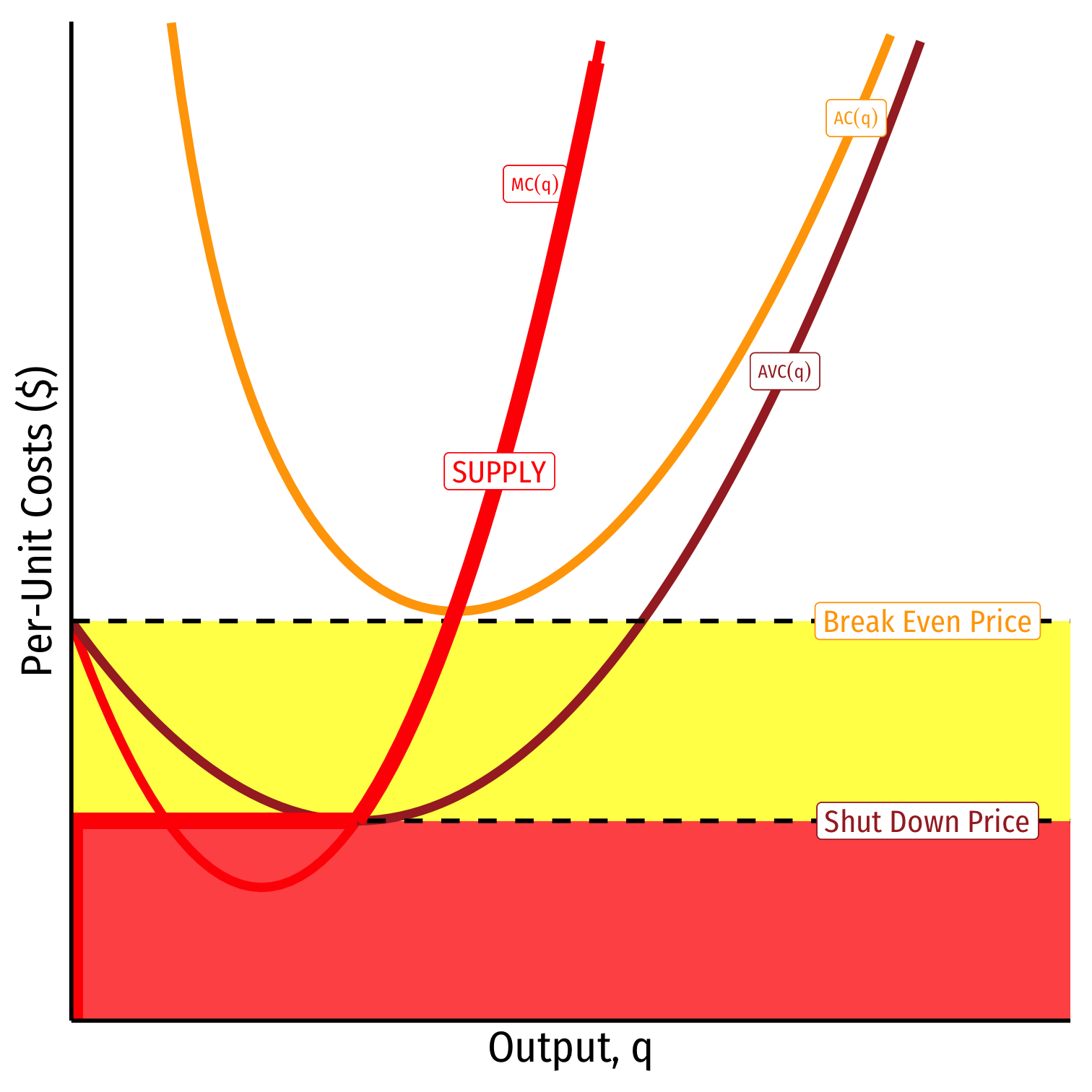
When AVC<p<AC

  • Profits are negative

  • Short run: continue production

    • Firm loses less π by producing than by not producing

  • Long run: firms in industry exit the industry

    • No new firms will enter this industry

Firm's Long Run Supply: Visualizing

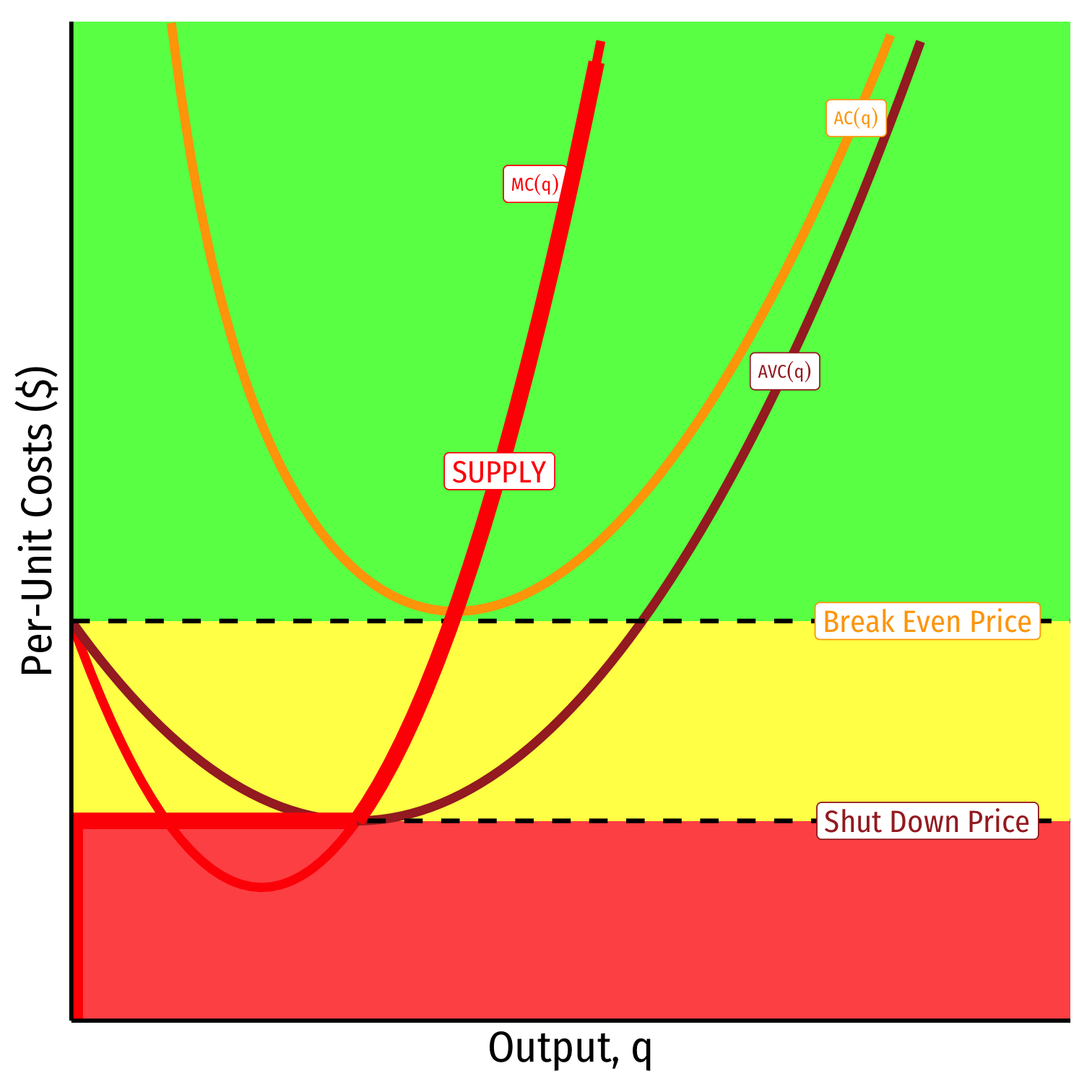
When AC<p

  • Profits are positive

  • Short run: continue production

    • Firm earn profits

  • Long run: firms in industry stay in industry

    • New new firms will enter this industry

Summary:

1. Choose q∗ such that MR(q)=MC(q)

Summary:

1. Choose q∗ such that MR(q)=MC(q)

2. Profit π=q[p−AC(q)]

Summary:

1. Choose q∗ such that MR(q)=MC(q)

2. Profit π=q[p−AC(q)]

3. Shut down in the short run if p<AVC(q)

Summary:

1. Choose q∗ such that MR(q)=MC(q)

2. Profit π=q[p−AC(q)]

3. Shut down in the short run if p<AVC(q)

Firm's short run (inverse) supply:

{p=MC(q)if p≥AVCq=0If p<AVC

Summary:

1. Choose q∗ such that MR(q)=MC(q)

2. Profit π=q[p−AC(q)]

3. Shut down in the short run if p<AVC(q)

Firm's short run (inverse) supply:

{p=MC(q)if p≥AVCq=0If p<AVC

4. Exit in the long run if p<AC(q)

Summary:

1. Choose q∗ such that MR(q)=MC(q)

2. Profit π=q[p−AC(q)]

3. Shut down in the short run if p<AVC(q)

Firm's short run (inverse) supply:

{p=MC(q)if p≥AVCq=0If p<AVC

4. Exit in the long run if p<AC(q)

Firm's long run (inverse) supply:

{p=MC(q)if p≥ACq=0If p<AC

Recall: The Two Major Models of Economics as a "Science"

Optimization

  • Agents have objectives they value

  • Agents face constraints

  • Make tradeoffs to maximize objectives within constraints

Recall: The Two Major Models of Economics as a "Science"

Optimization

  • Agents have objectives they value

  • Agents face constraints

  • Make tradeoffs to maximize objectives within constraints

Equilibrium

  • Agents face competition from others that affect prices

  • Agents adjust their behaviors based on prices

  • Stable outcomes result where all agents cease adjusting

Recall: Optimization and Equilibrium

  • If people can learn and change their behavior, they will always switch to a higher-valued option

  • If there are no alternatives that are better, people are at an optimum

  • If everyone is at an optimum, the system is in equilibrium

Market Entry and Exit

Exit, Entry, and Long Run Industry Equilibrium I

  • Now we must combine optimizing individual firms with market-wide adjustment to equilibrium

  • Since π=[p−AC(q)]q, in the long run, profit-seeking firms will:

Exit, Entry, and Long Run Industry Equilibrium I

  • Now we must combine optimizing individual firms with market-wide adjustment to equilibrium

  • Since π=[p−AC(q)]q, in the long run, profit-seeking firms will:

    • Enter markets where p>AC(q)

Exit, Entry, and Long Run Industry Equilibrium I

  • Now we must combine optimizing individual firms with market-wide adjustment to equilibrium

  • Since π=[p−AC(q)]q, in the long run, profit-seeking firms will:

    • Enter markets where p>AC(q)
    • Exit markets where p<AC(q)

Exit, Entry, and Long Run Industry Equilibrium II

  • Long-run equilibrium: entry and exist cases when p=AC(q) for all firms, implying normal economic profits of π=0

Exit, Entry, and Long Run Industry Equilibrium II

  • Long-run equilibrium: entry and exist cases when p=AC(q) for all firms, implying normal economic profits of π=0

  • Zero Profits Theorem: long run economic profits for all firms in a competitive industry are 0

  • Firms must earn an accounting profit to stay in business

  • A constant tendency as output prices are pushed down and input prices are bid up, squeezing economic profits to 0

  • In real life, constant changes in underlying prices, technology, preferences

The Industry Supply Curve

  • Industry supply curve: sum of all individual firms' supply curves (MC(q) curve above AVCmin)

  • To keep it simple on the following slides:

    • assume no fixed costs, so AC(q)=AVC(q)
    • then industry supply curve is sum of individual MC(q) curves above AC(q)min
    • see 2.4 class notes for more explanation

Industry Supply Curves (Identical Firms)









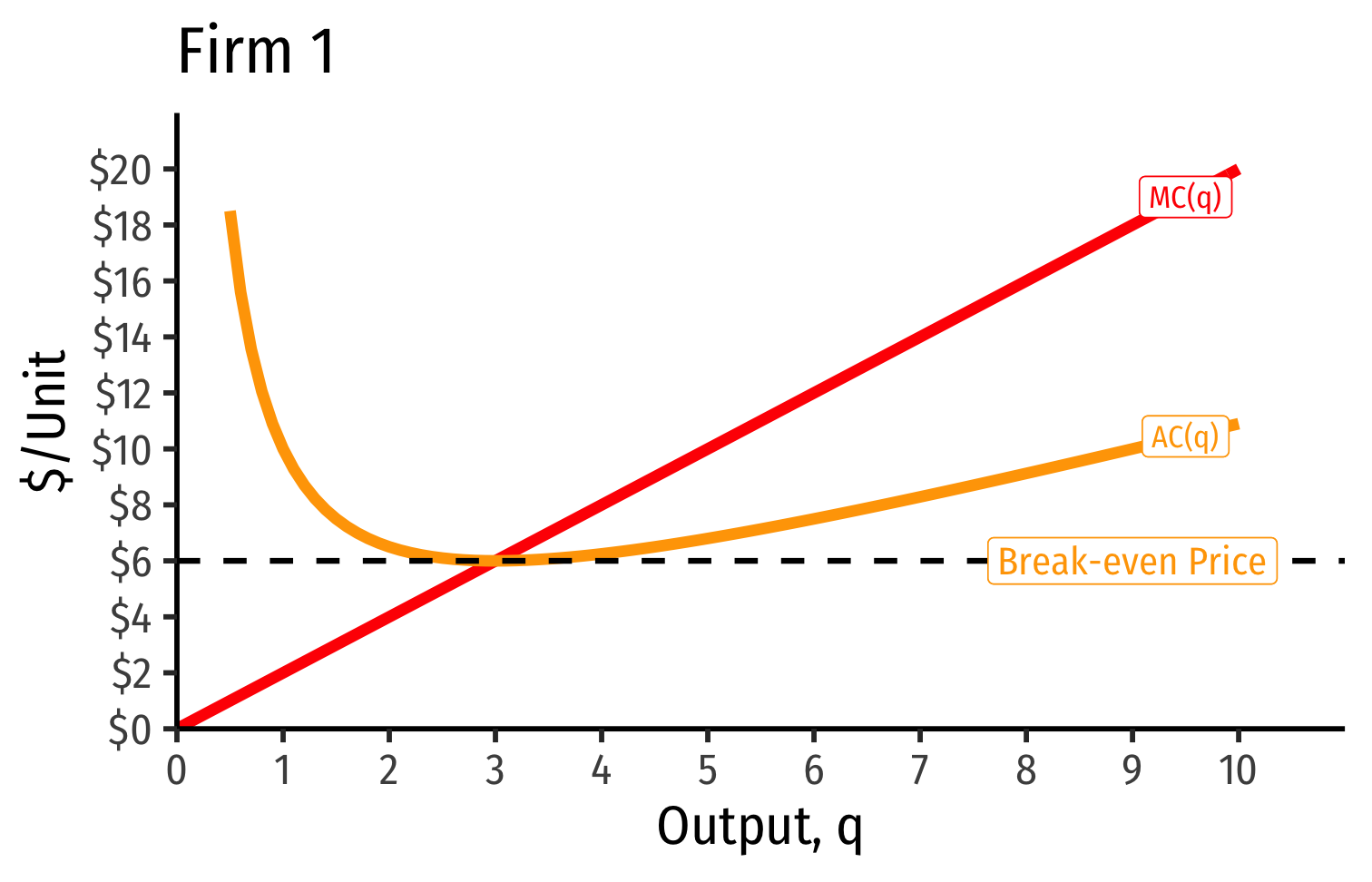
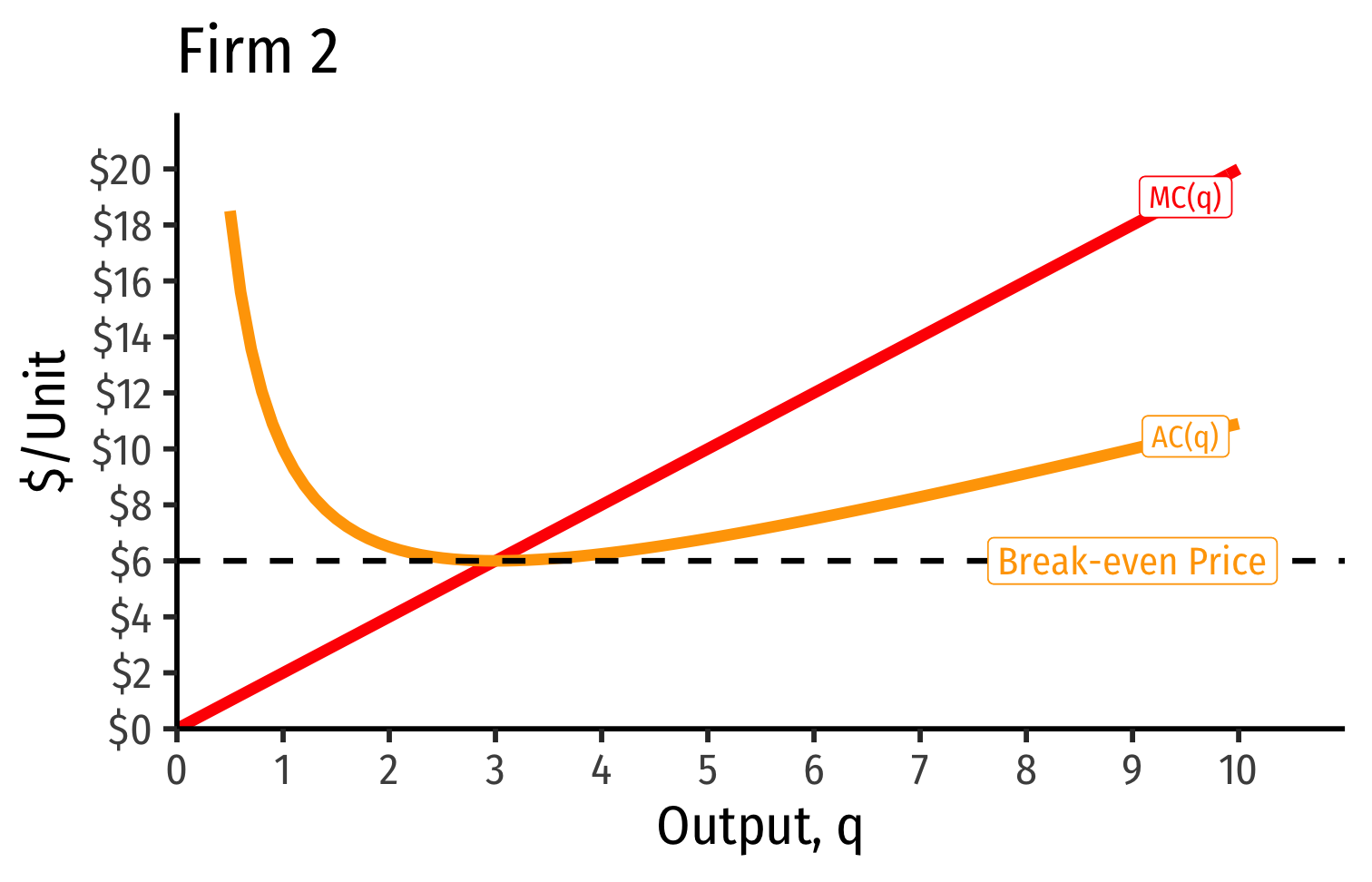
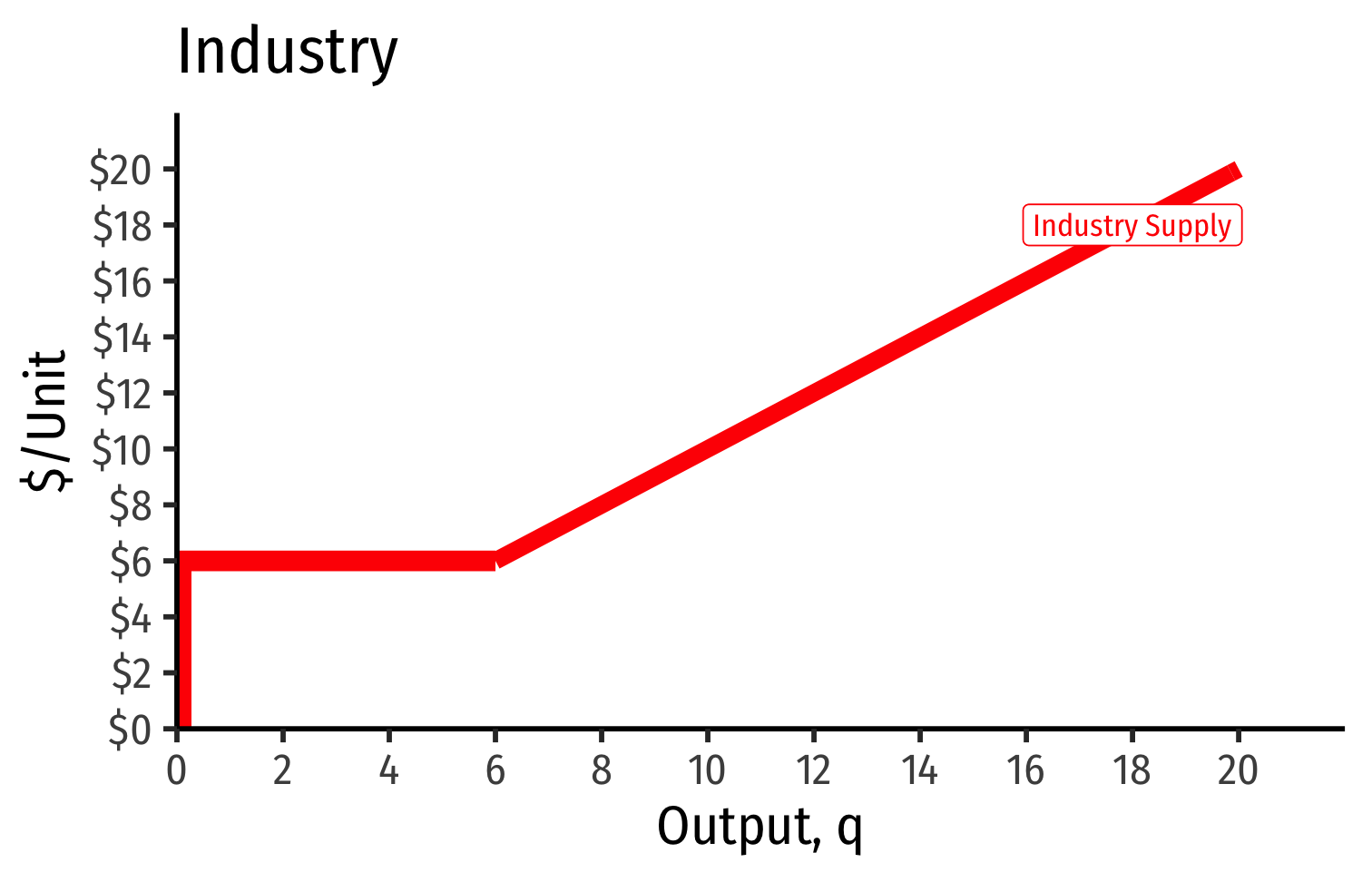
Industry Supply Curves (Identical Firms)









  • Industry supply curve is the horizontal sum of all individual firm's supply curves
    • Which are each firm's marginal cost curve above its breakeven price

Industry Supply Curves (Identical Firms)









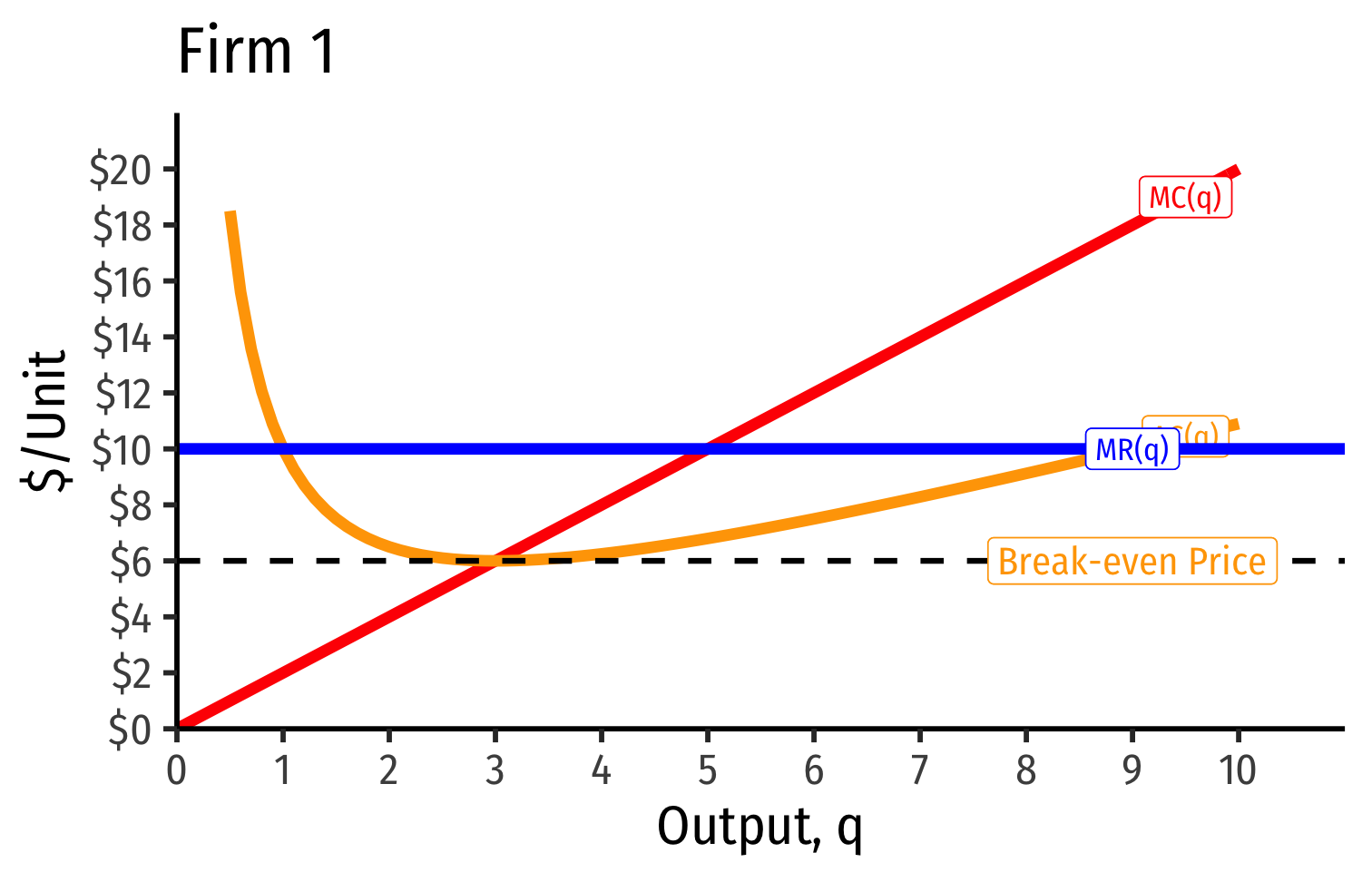
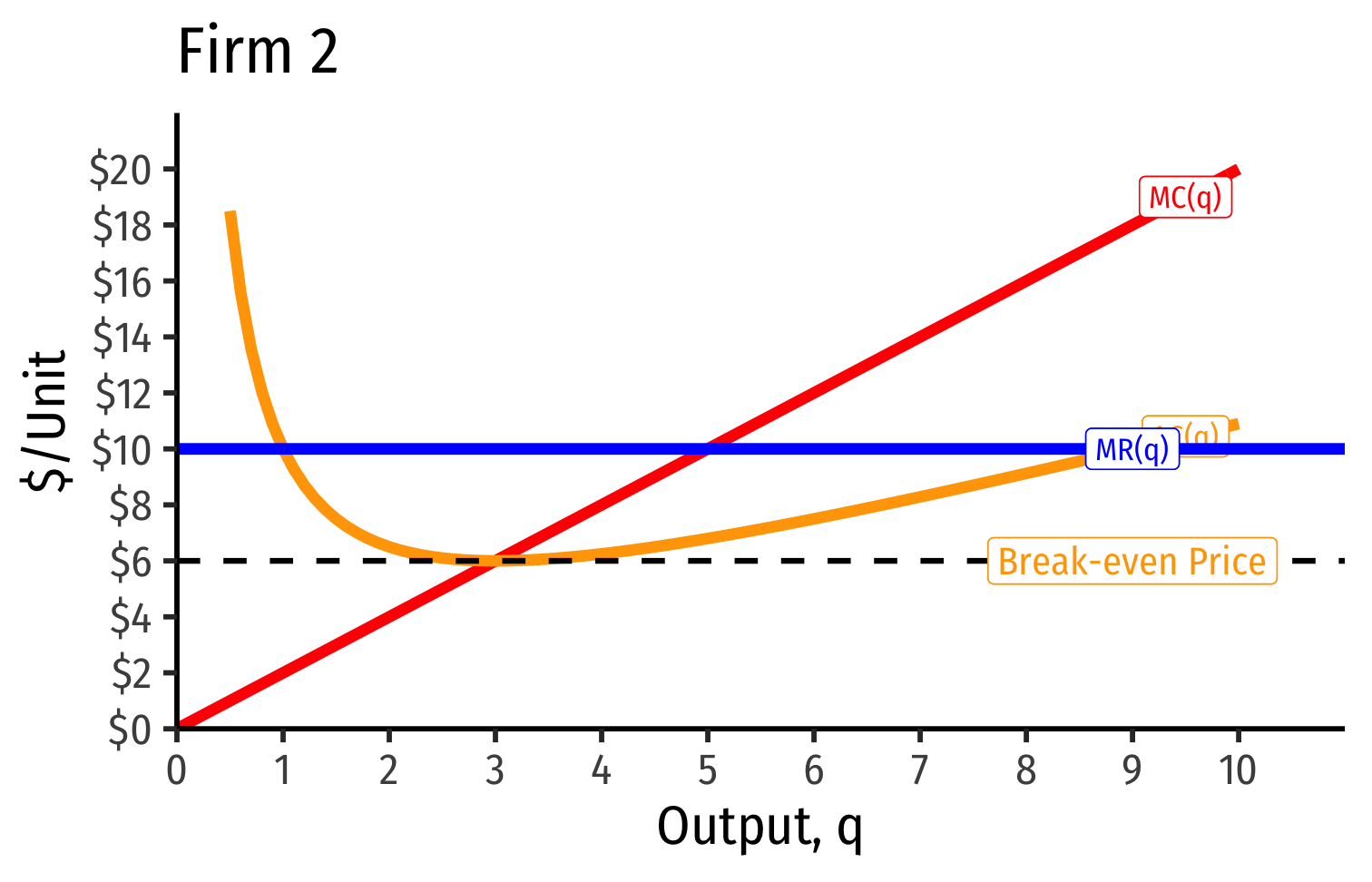
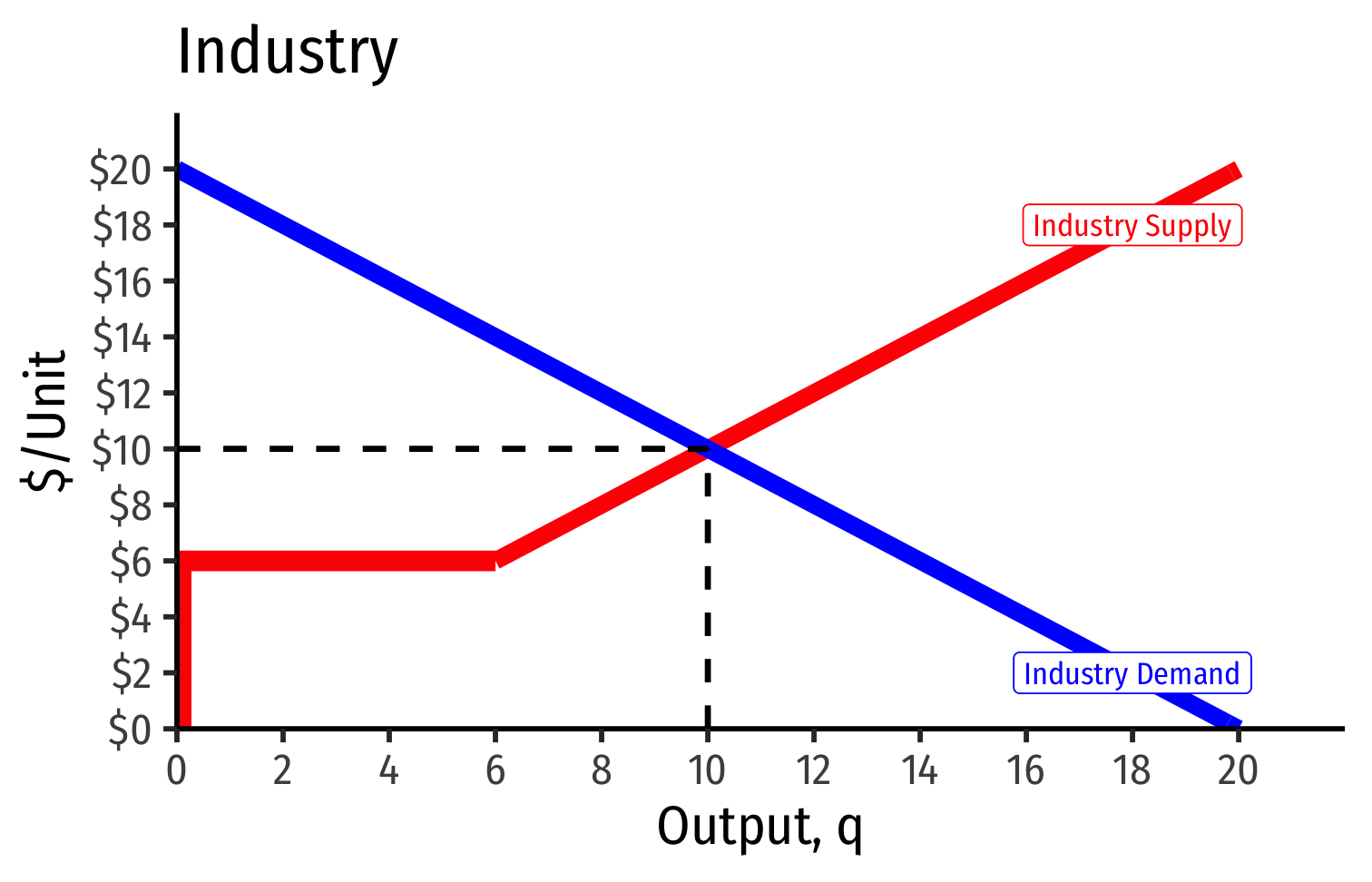
  • Industry demand curve (where equal to supply curve) sets market price, demand for each firm

Industry Supply Curves (Identical Firms)









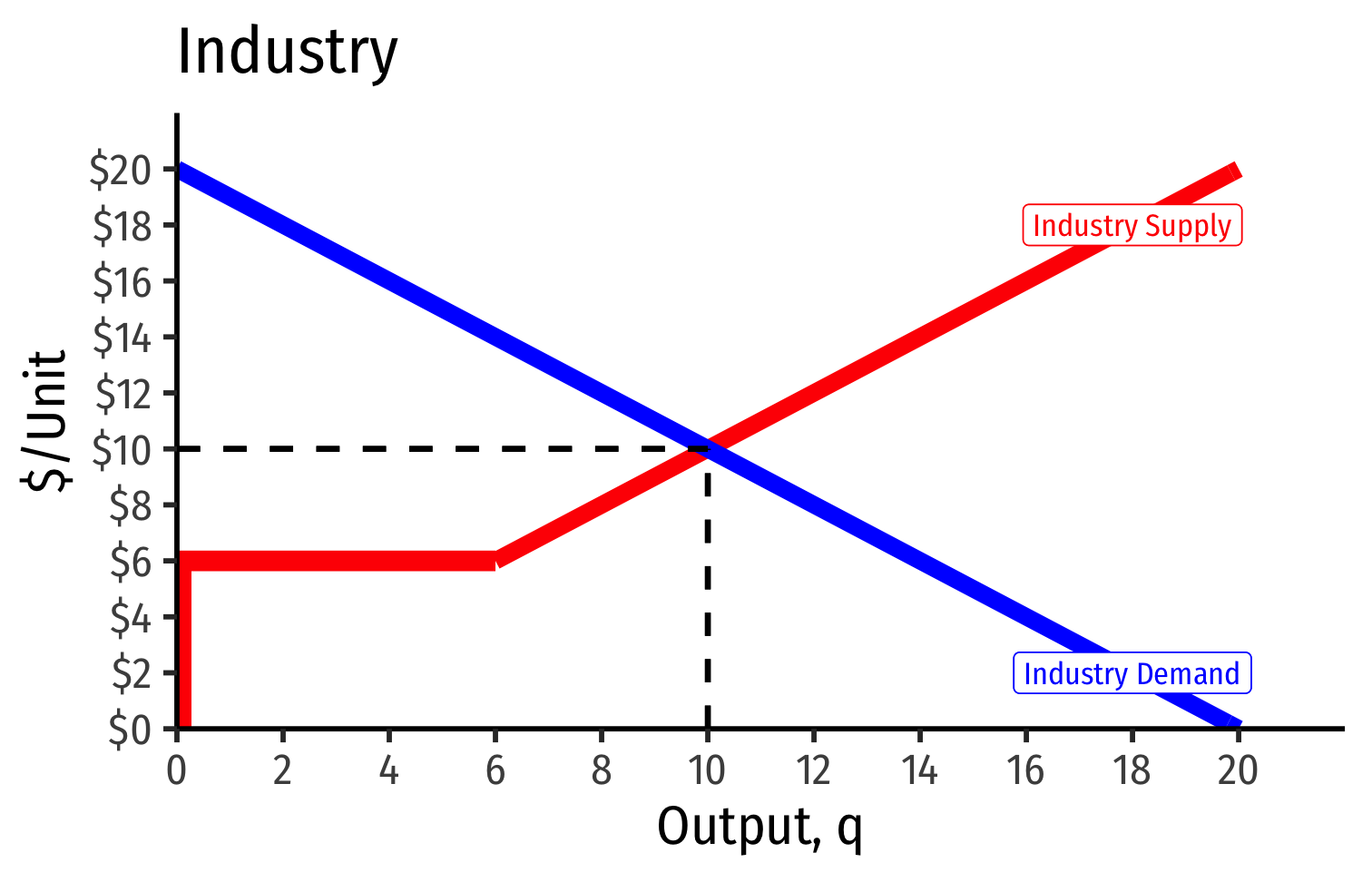
  • Industry demand curve (where equal to supply curve) sets market price, demand for each firm

  • Short Run: each firm is earning profits p>AC(q)

  • Long run: induces entry by firm 3, firm 4, ⋯, firm n

Industry Supply Curves (Identical Firms)









  • Industry demand curve (where equal to supply curve) sets market price, demand for each firm

  • Short Run: each firm is earning profits p>AC(q)

  • Long run: induces entry by firm 3, firm 4, ⋯, firm n

  • Long run industry equilibrium:

Industry Supply Curves (Identical Firms)









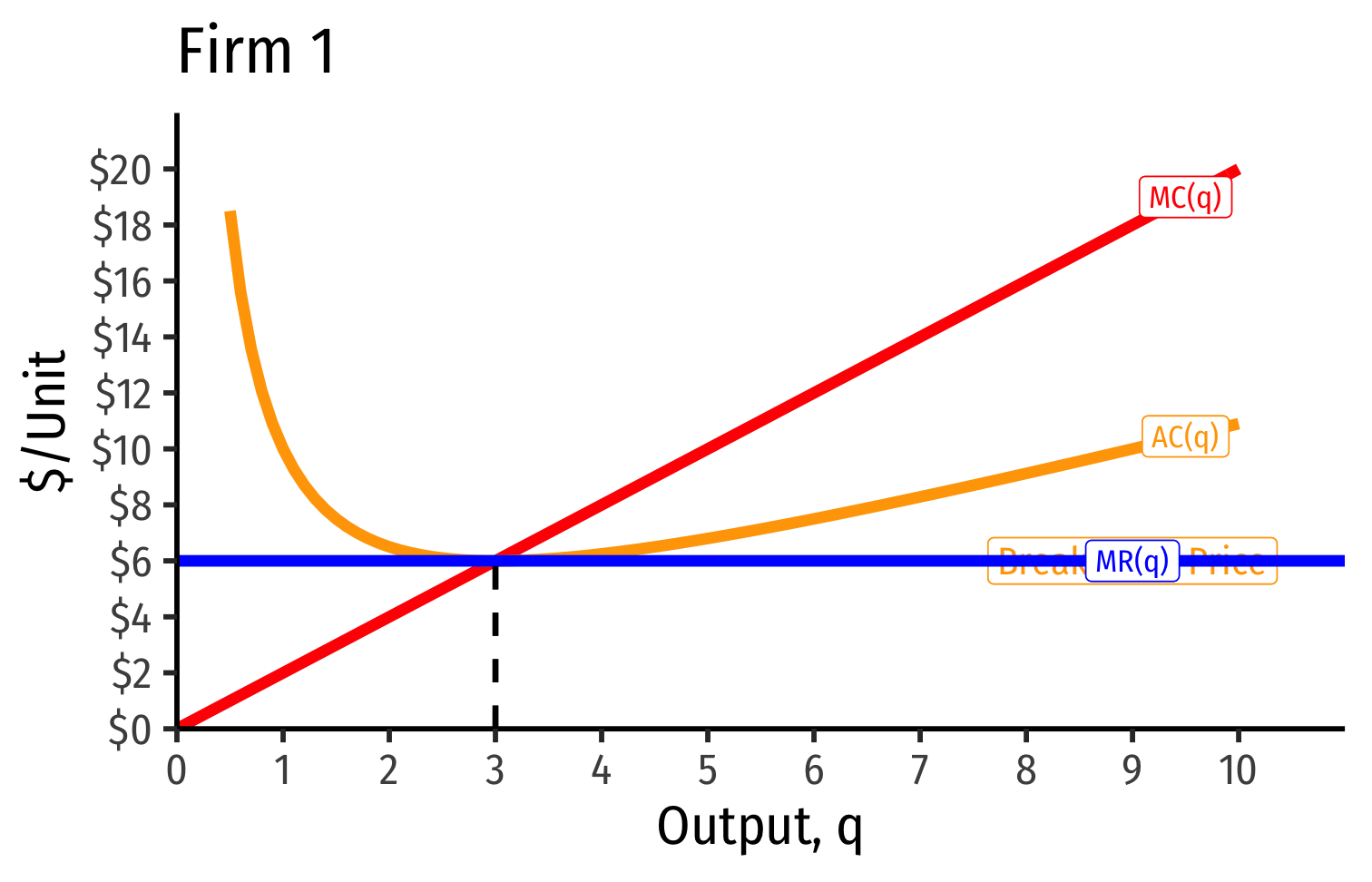
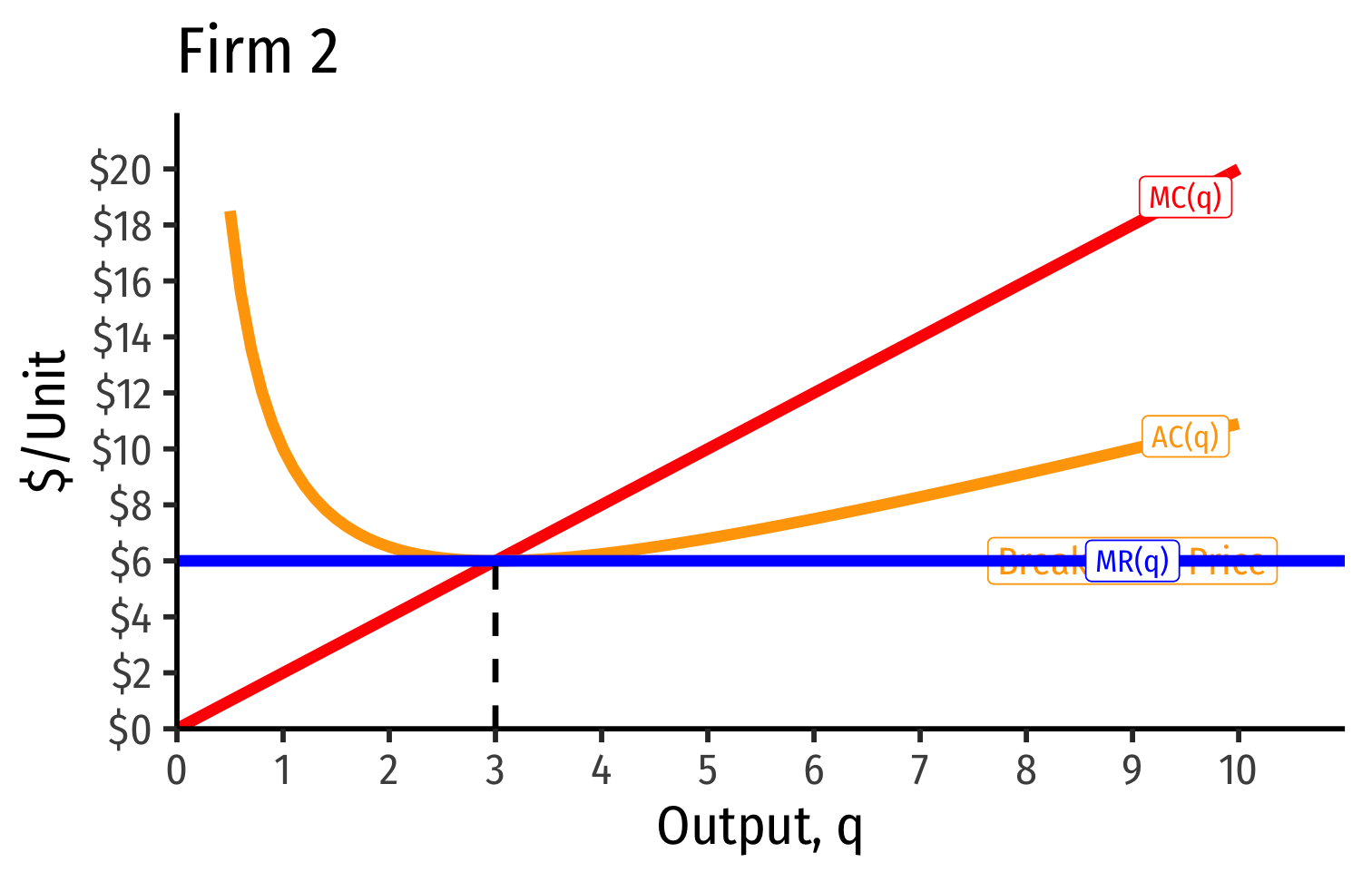
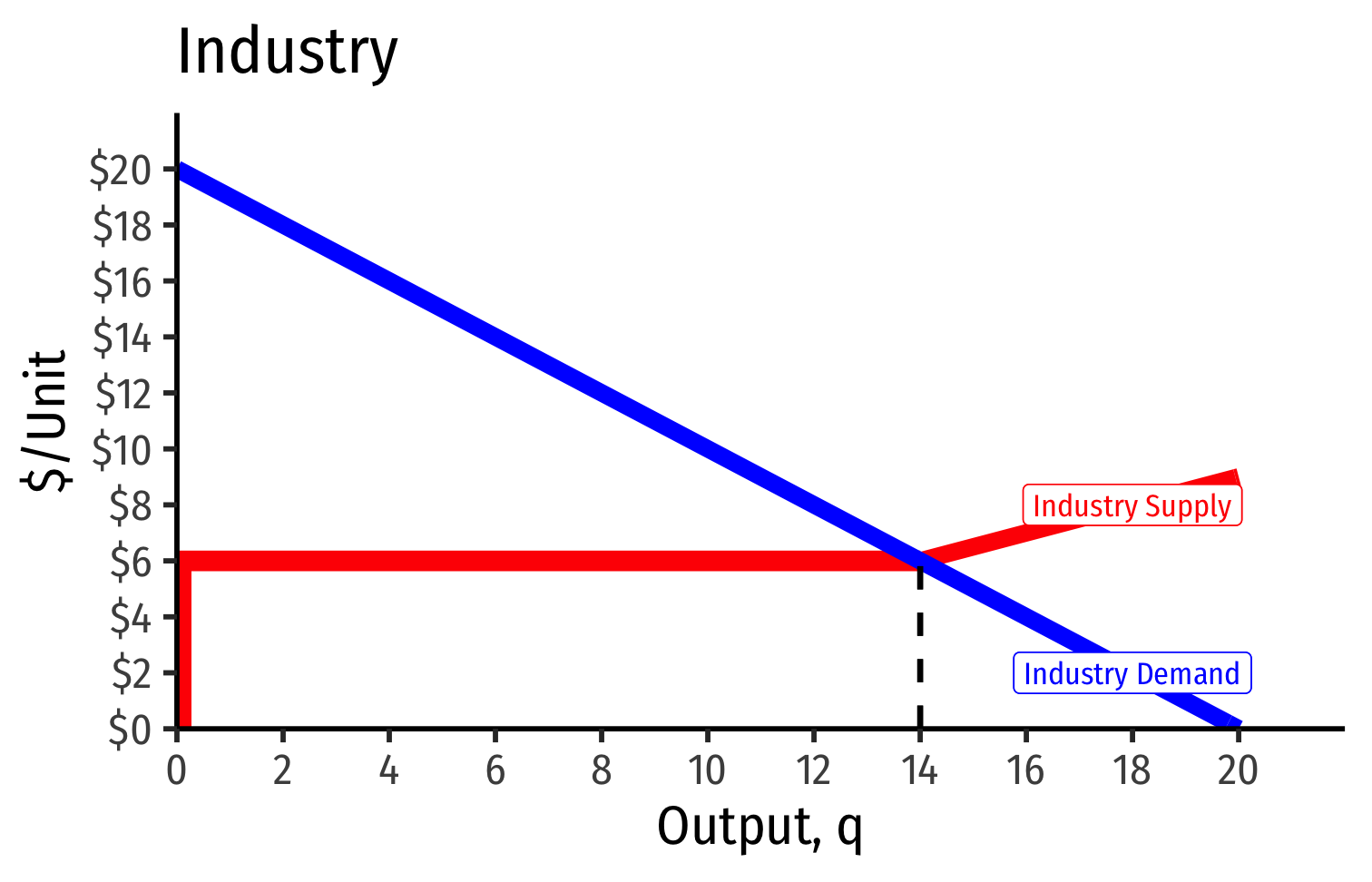
  • Industry demand curve (where equal to supply curve) sets market price, demand for each firm

  • Short Run: each firm is earning profits p>AC(q)

  • Long run: induces entry by firm 3, firm 4, ⋯, firm n

  • Long run industry equilibrium: p=AC(q)min, π=0 at p= $6

    • Supply becomes more elastic (more firms supplying more output)

Zero Profit Theorem & Economic Rents

Industry Supply Curves (Different Firms) I

  • Firms may have different cost structures due to differences in:
    • Managerial talent
    • Worker talent
    • Location
    • First-mover advantage
    • Technological secrets/IP
    • License/permit access
    • Political connections
    • Lobbying

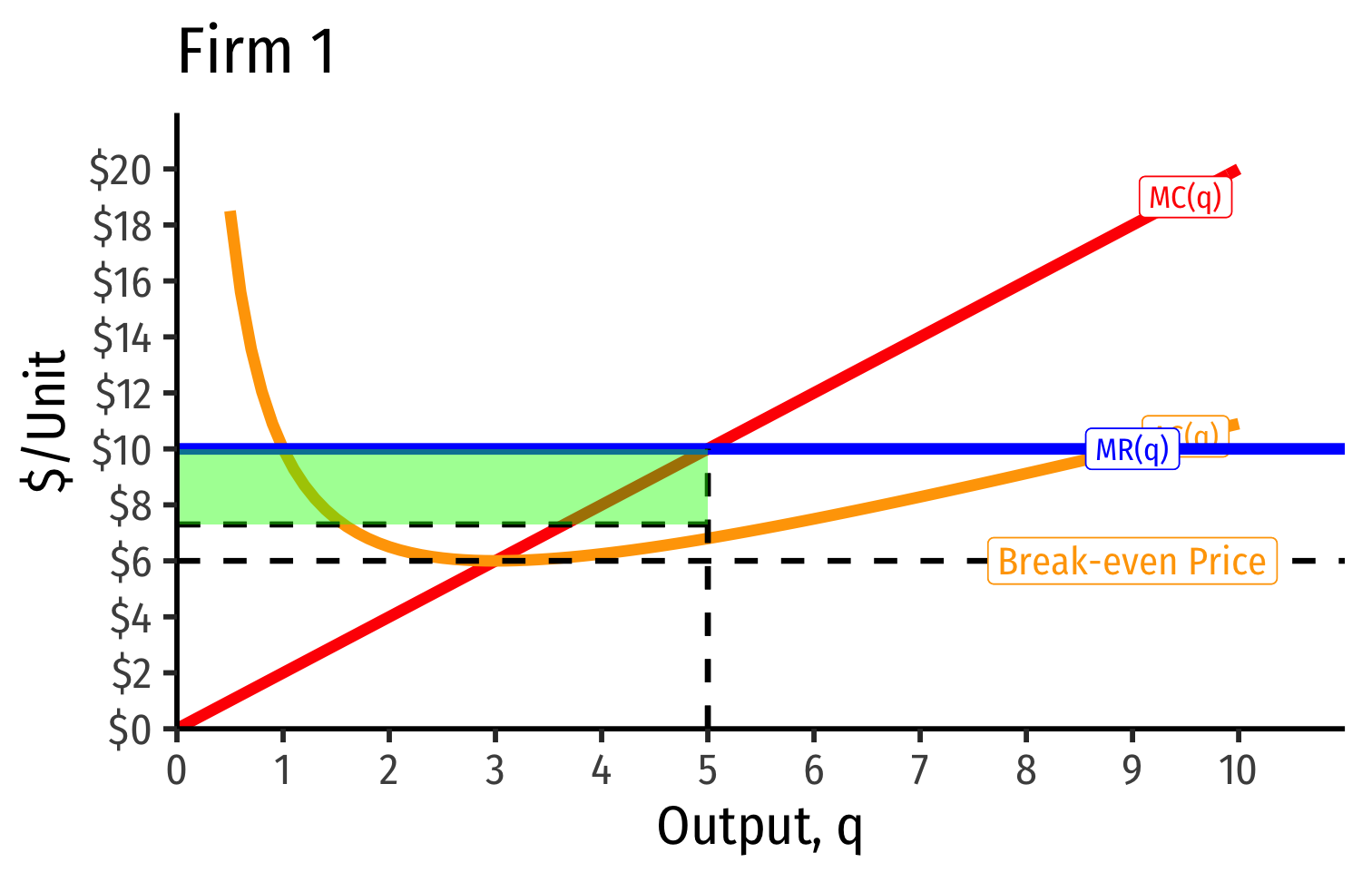
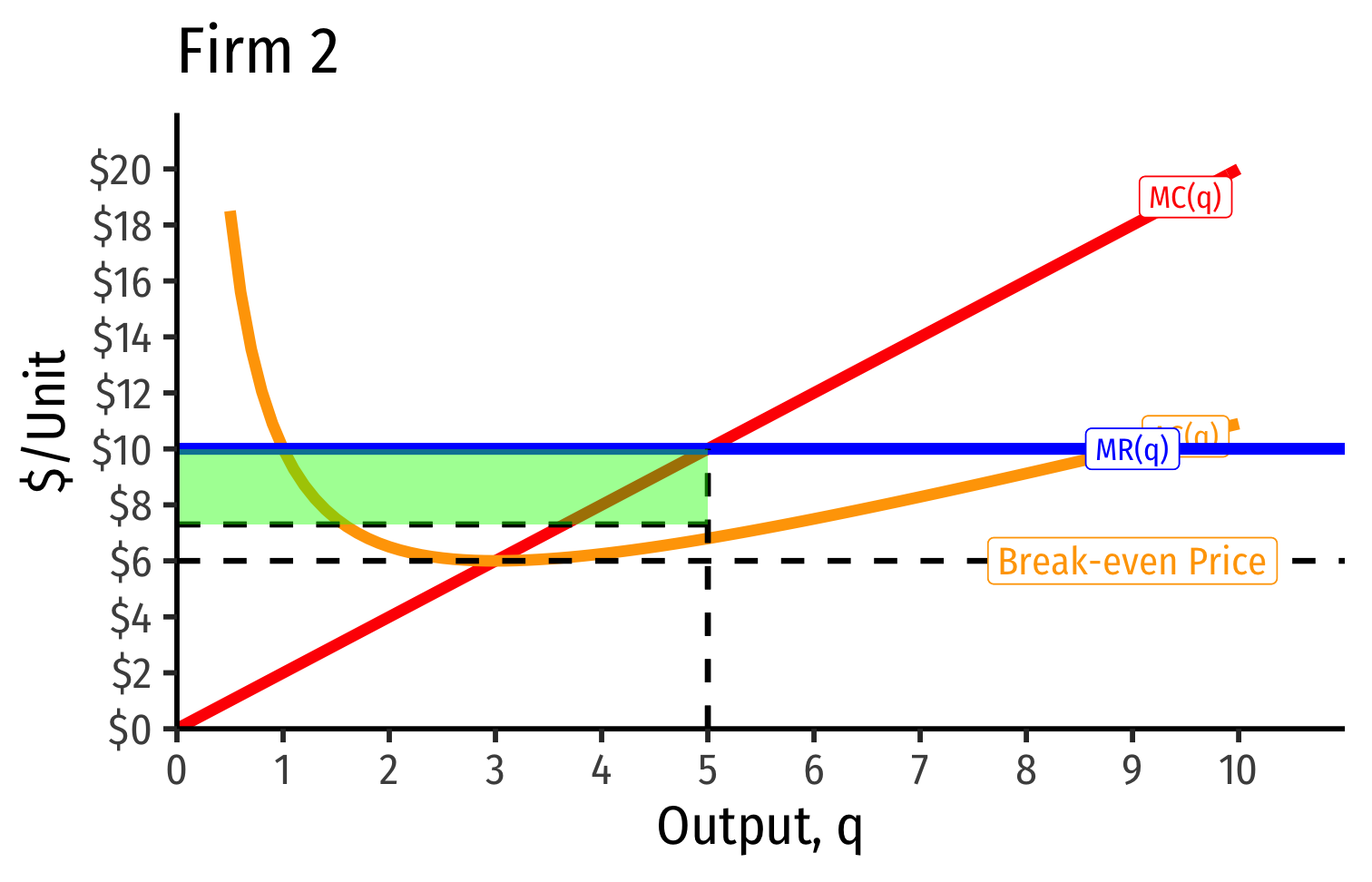
Industry Supply Curves (Different Firms) II









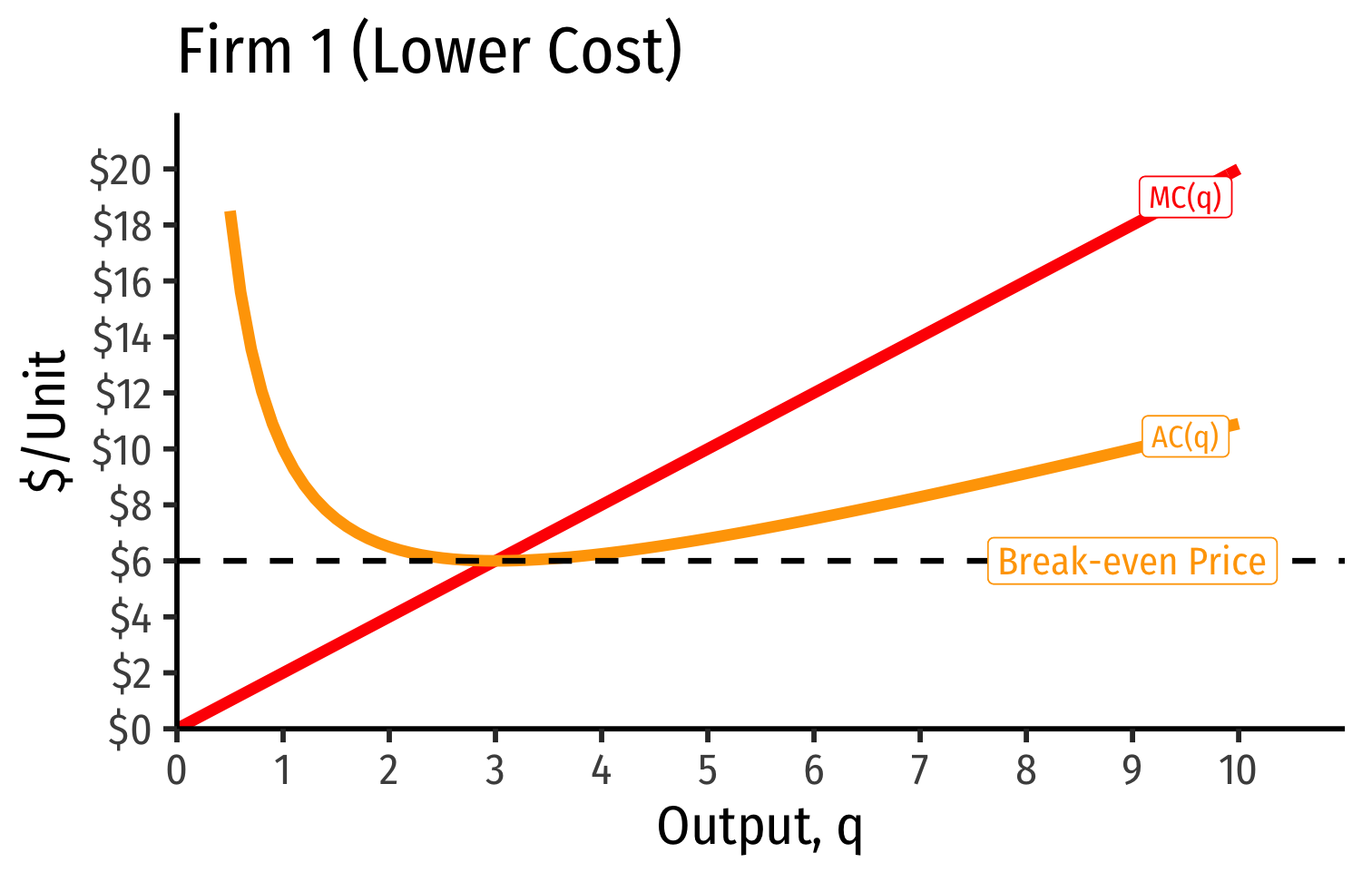
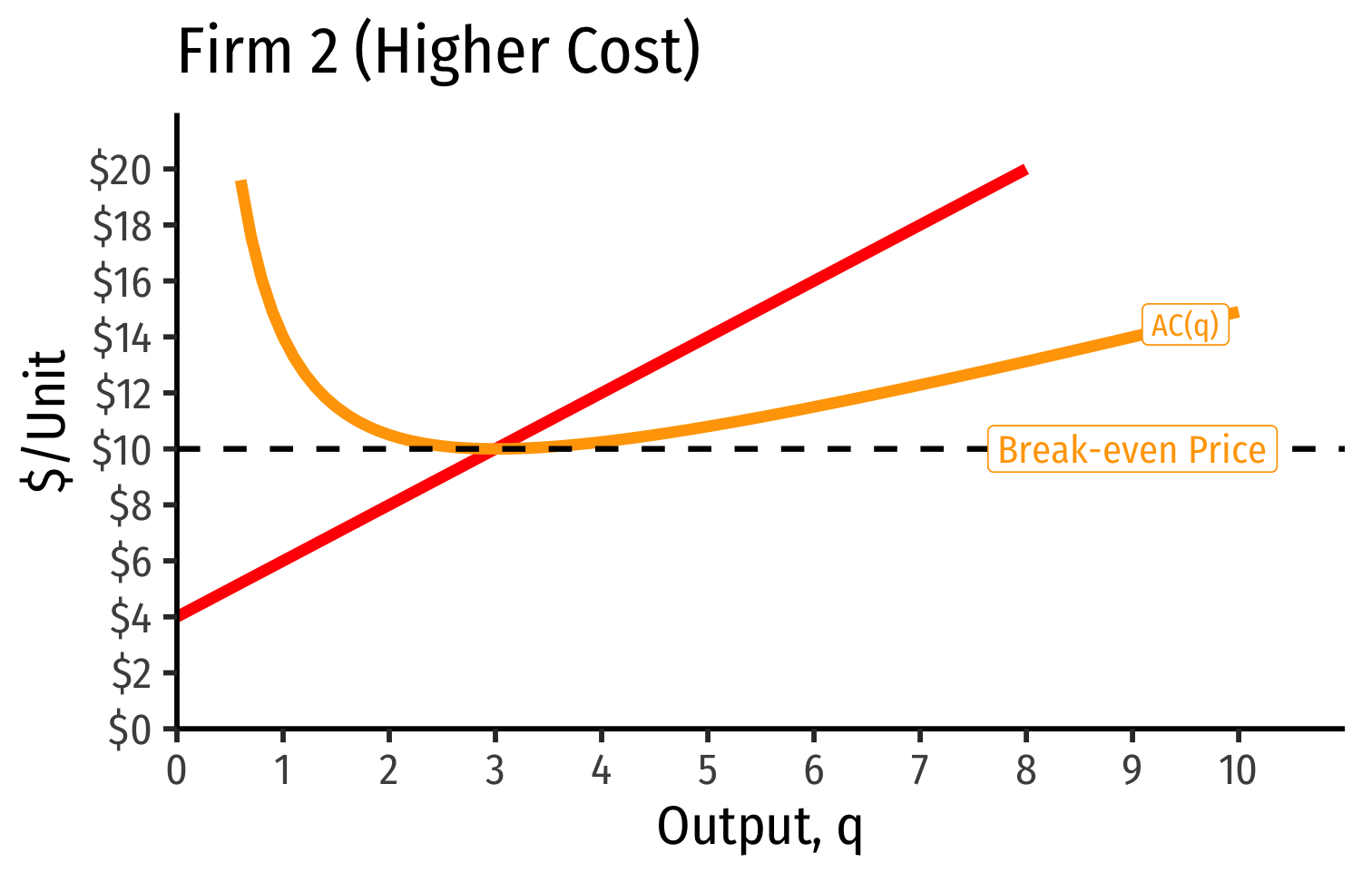
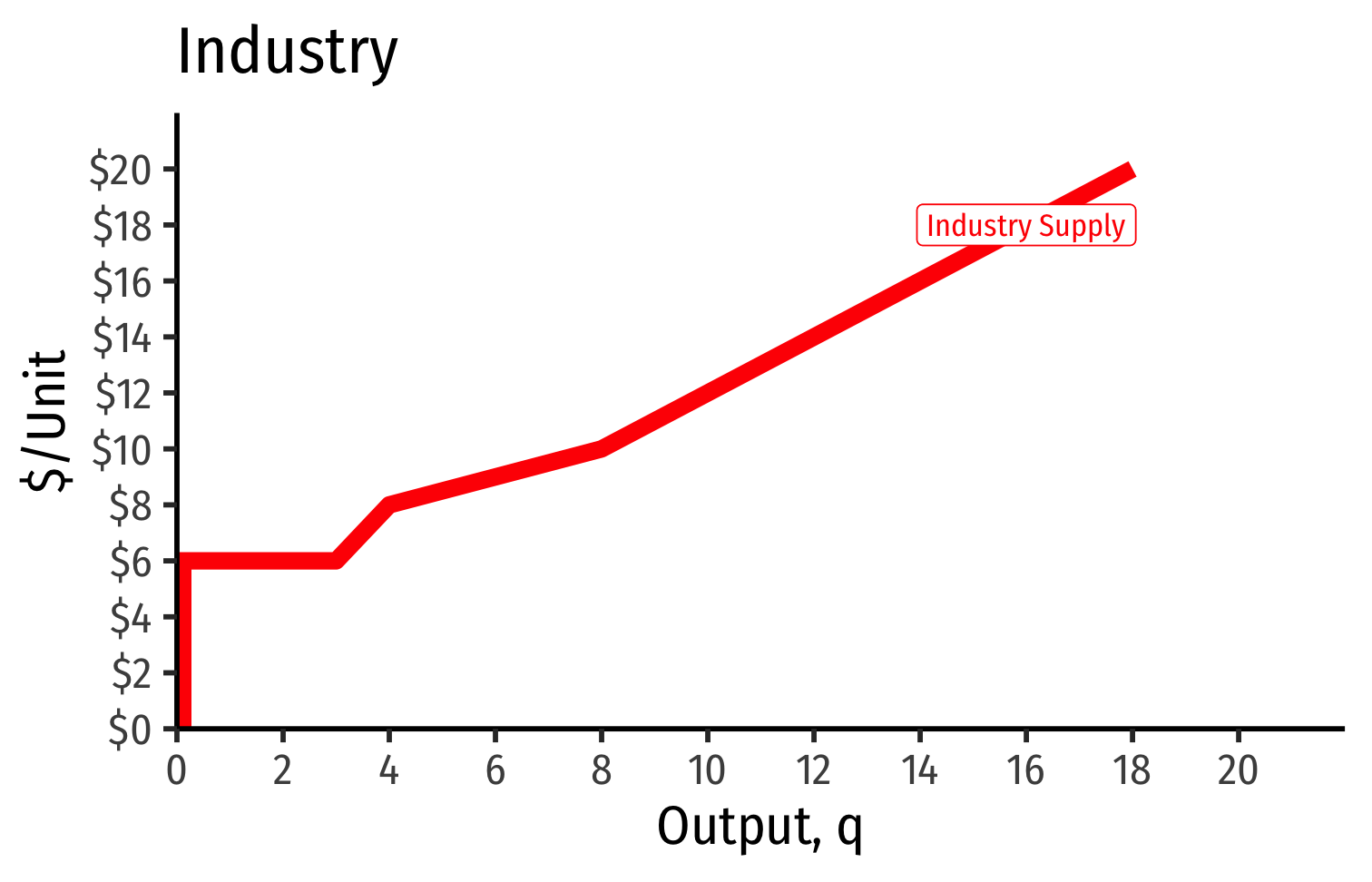
Industry Supply Curves (Different Firms) II









  • Industry supply curve is the horizontal sum of all individual firm's supply curves
    • Which are each firm's marginal cost curve above its breakeven price

Industry Supply Curves (Different Firms) II









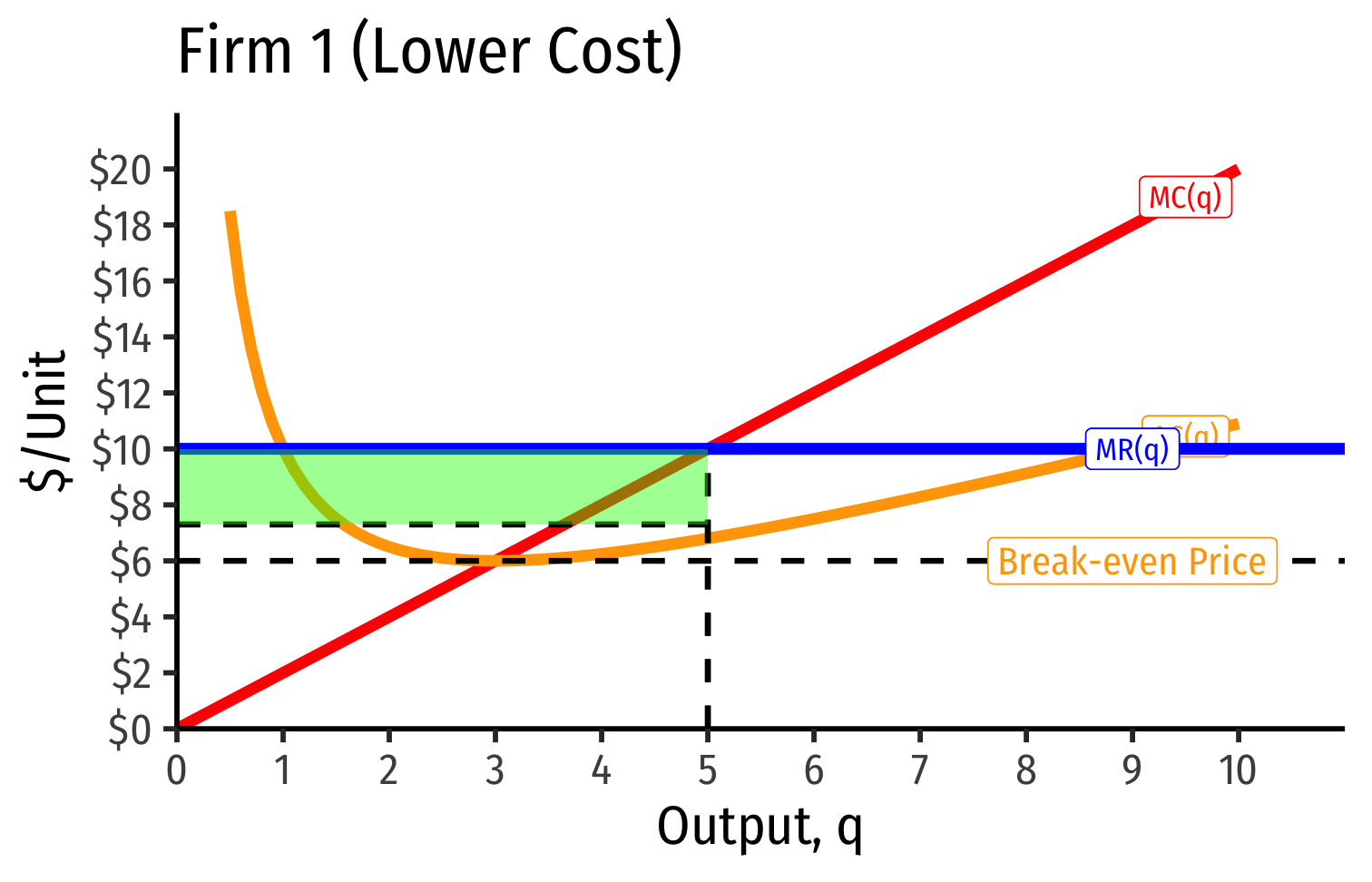
Industry Supply Curves (Different Firms) II









  • Industry demand curve (where equal to supply curve) sets market price, demand for each firm

Industry Supply Curves (Different Firms) II









  • Industry demand curve (where equal to supply curve) sets market price, demand for each firm

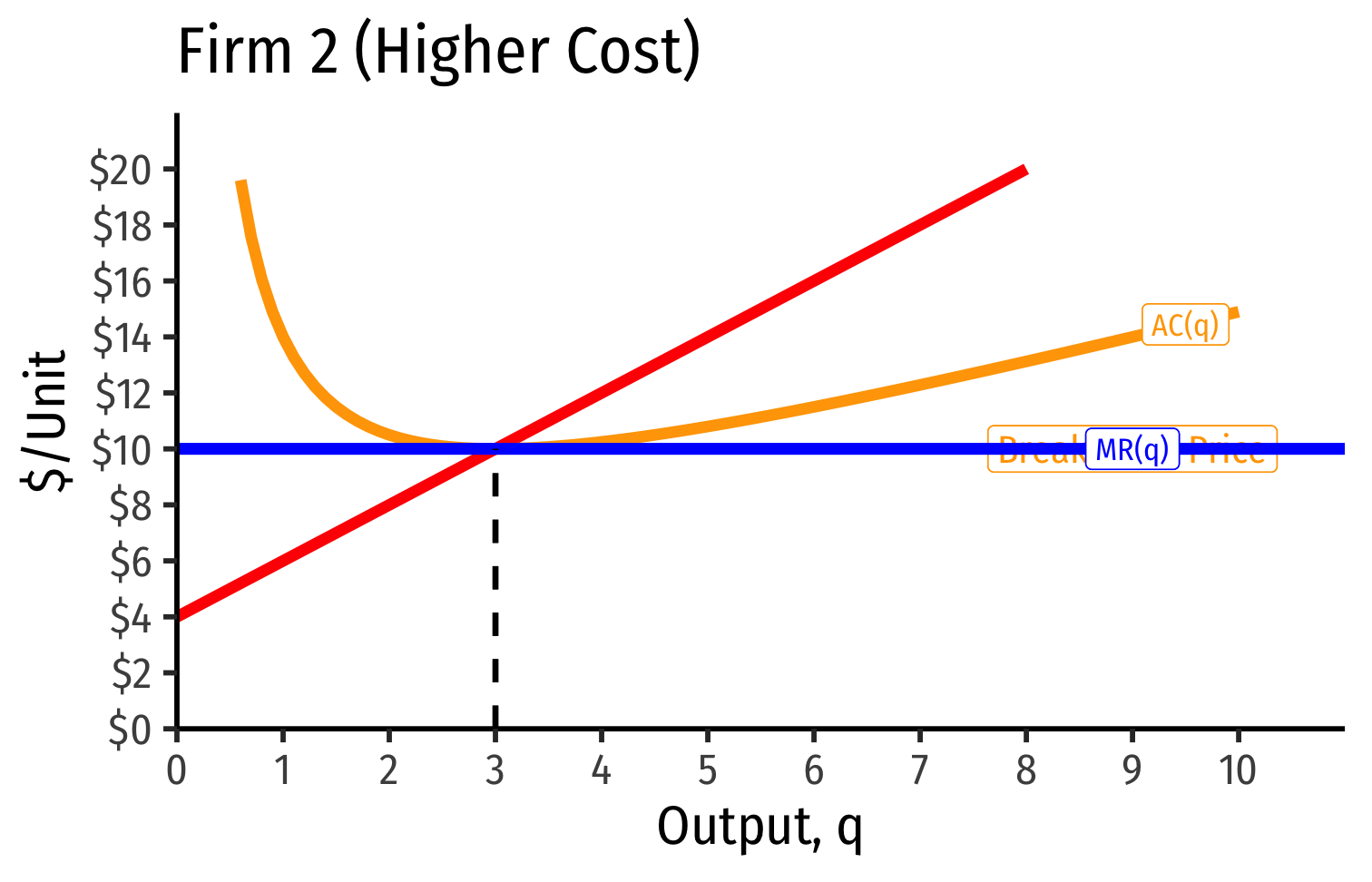
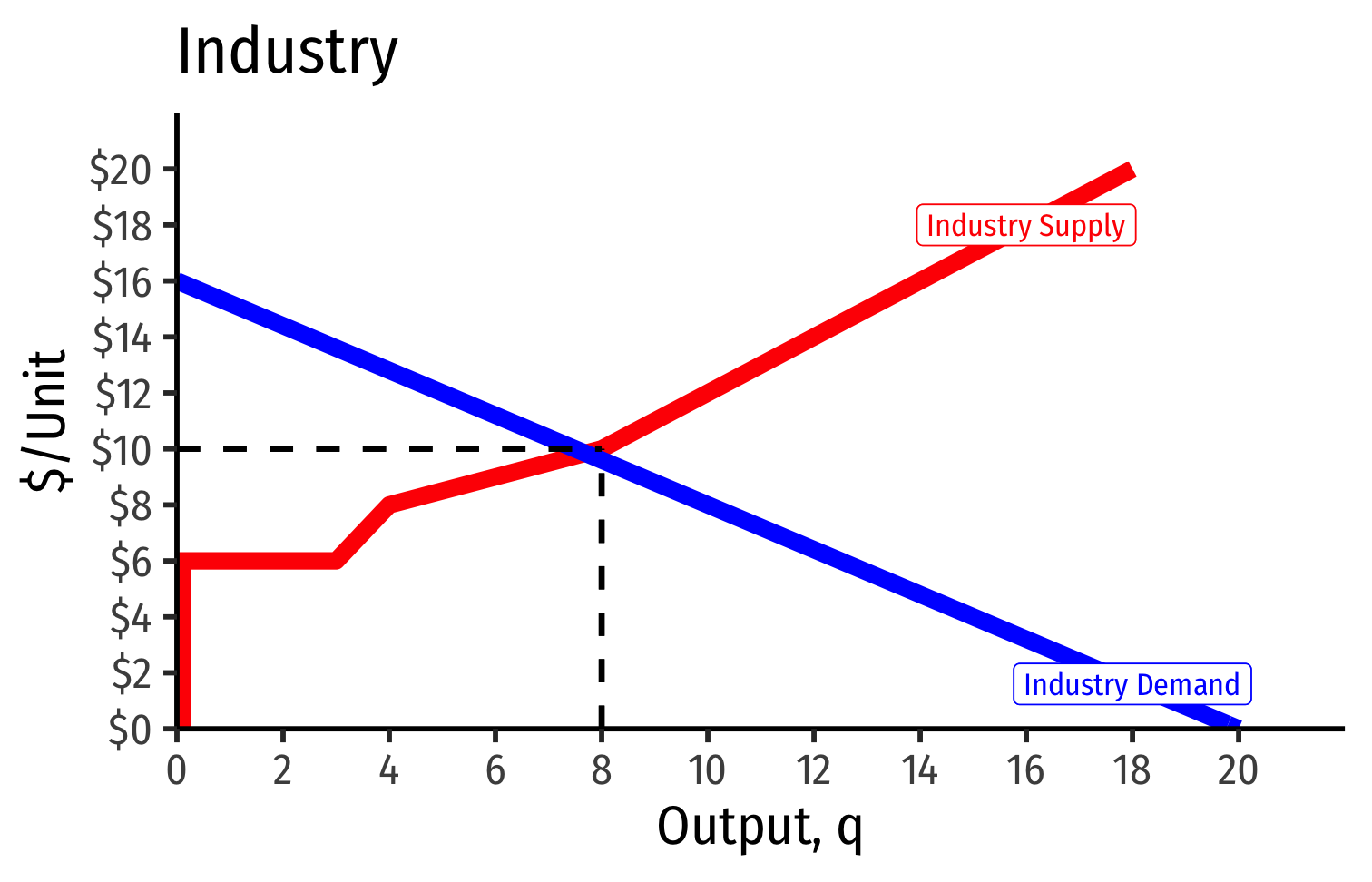
  • Long run industry equilibrium: p=AC(q)min, π=0 for marginal (highest cost) firm (Firm 2)

Industry Supply Curves (Different Firms) II









  • Industry demand curve (where equal to supply curve) sets market price, demand for each firm

  • Long run industry equilibrium: p=AC(q)min, π=0 for marginal (highest cost) firm (Firm 2)

  • Firm 1 (lower cost) appears to be earning profits

Economic Rents and Zero Economic Profits I

  • With differences between firms, long-run equilibrium p=AC(q)min of the marginal (highest-cost) firm

    • If p>AC(q) for that firm, would induce more entry into industry!

  • "Inframarginal" (lower-cost) firms earn economic rents: returns higher than their opportunity cost (what is needed to bring them online

    • p>AC(q)

  • Economic rents arise from relative differences between firms

Economic Rents and Zero Economic Profits II

  • Relatively scarce factors in the economy (talent, location, secrets, IP, licenses, being first, political favoritism, lobbying)

  • Inframarginal firms using the scarce factors gain a cost-advantage

  • It would seem these firms earn profits as other firms have higher costs

  • But what will happen to the prices for the scarce factors?

Rent: Microeconomics IV

  • Rents ≠ profits!

  • Rival firms willing to pay for rent-generating factor to gain advantage

  • Rents are included in the opportunity cost (price) for inputs

  • Firm does not earn the rents, they raise firm's costs and squeeze out profits!

  • Factor owners (workers, landowners, inventors, etc) earn the rents as higher payments for their services (wages, rents, interest, royalties, etc).

Recall: Accounting vs. Economic Point of View

  • Helpful to consider two points of view:
    • "Accounting point of view": are you taking in more cash than you are spending?
    • "Economic point of view: is your product you making the best social use of your resources (i.e. are there higher-valued uses of your resources you are keeping them away from)?

Entry Effects & External Economies

Entry/Exit Effects on Market Price

  • Firms entering or exiting an industry have an effect on the new market price

  • Think about basic supply & demand graphs:

    • Entry: ↑ industry supply ⟹ ↑q,↓p
    • Exit: ↓ industry supply ⟹ ↓q,↑p

External Economies

  • How large this change in price will be from entry/exit depends on industry-wide costs and external economies

  • Economies of scale are internal to the firm (a firm's own average cost curve)

  • External economies have to do with how the size of the entire industry affects all individual firm's costs

    • These are externalities that spill over across all firms in an industry

  • Three possibilities

Constant Cost Industry (No External Economies) I

  • Constant cost industry has no external economies, no change in costs as industry output increases (firms enter & incumbents produce more)

  • A perfectly elastic long-run industry supply curve!

  • Determinants:

    • Industry's purchases are not a large share of input markets
    • Often constant marginal costs, insignificant fixed costs

  • Examples: toothpicks, domain name registration, waitstaff

Constant Cost Industry (No External Economies) II

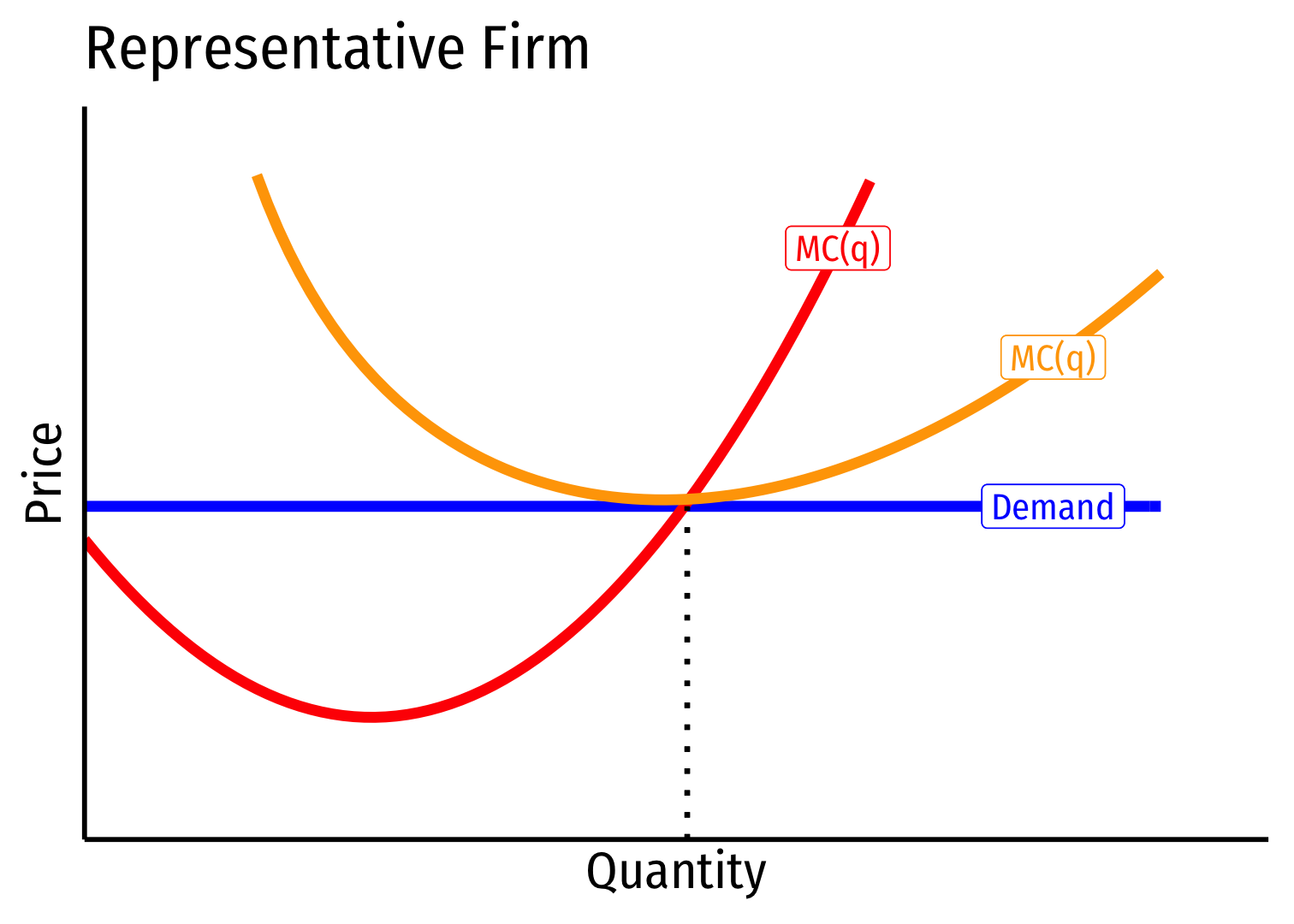
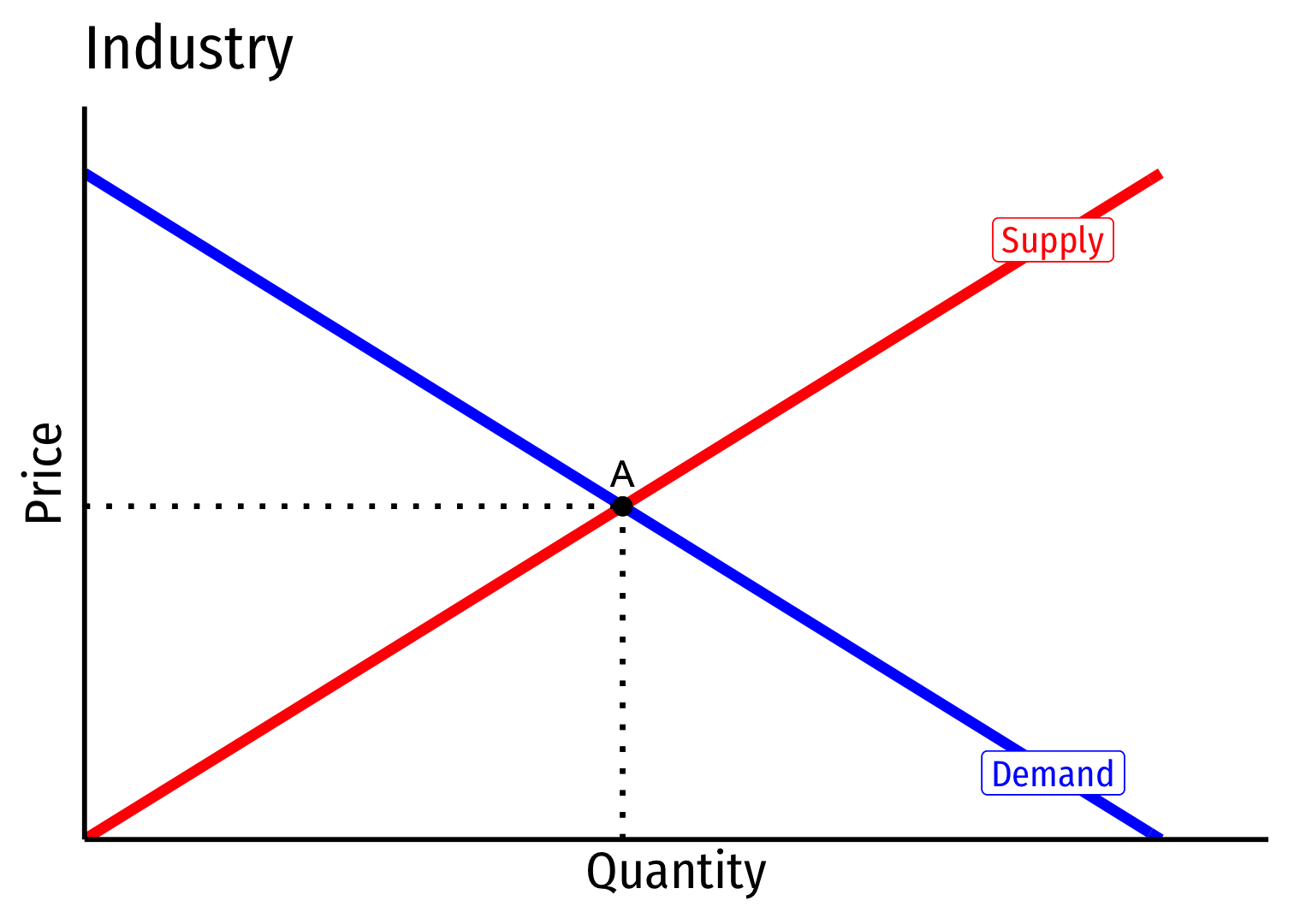
  • Industry equilibrium: firms earning normal π=0,p=MC(q)=AC(q)

Constant Cost Industry (No External Economies) III

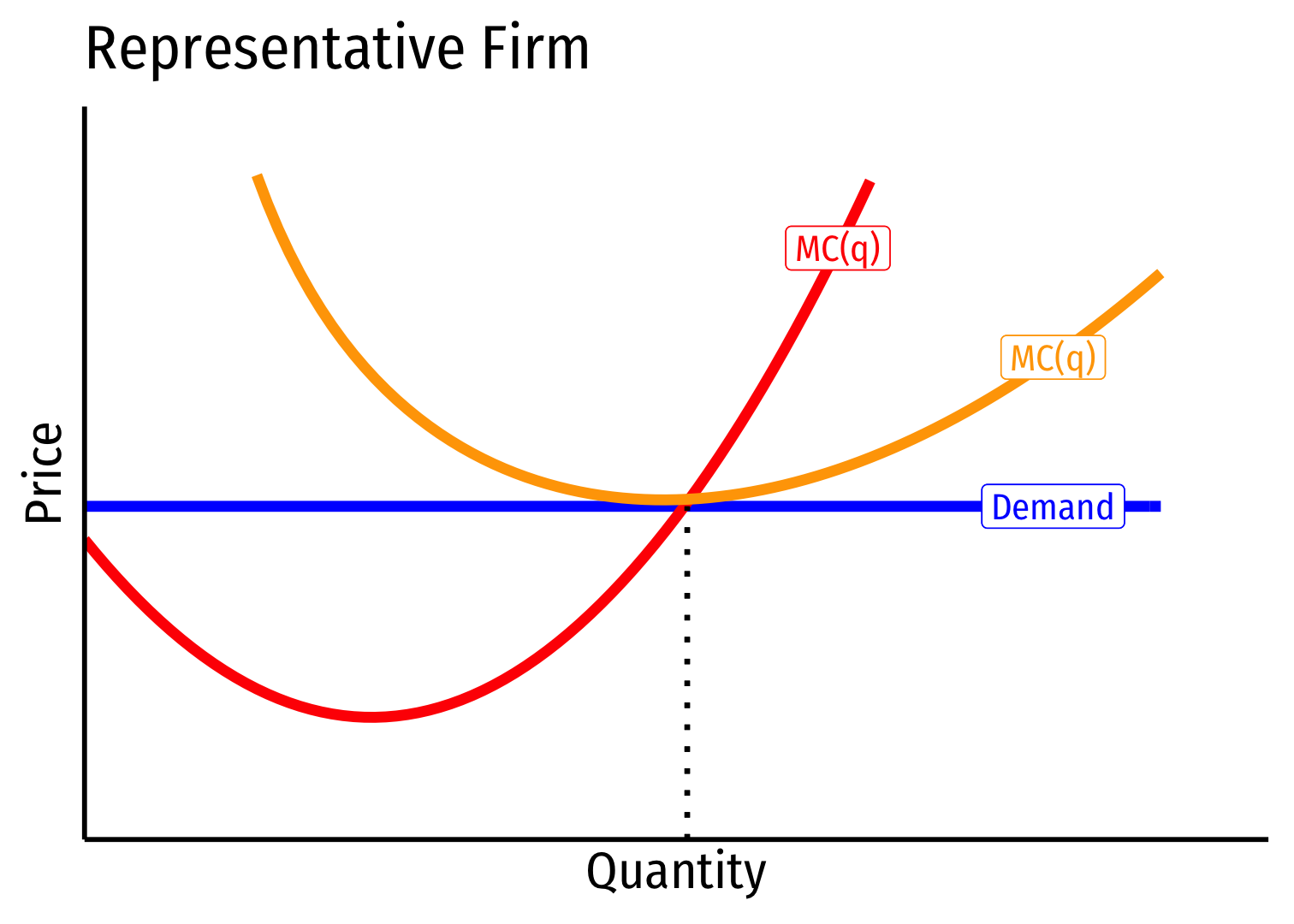
  • Industry equilibrium: firms earning normal π=0,p=MC(q)=AC(q)

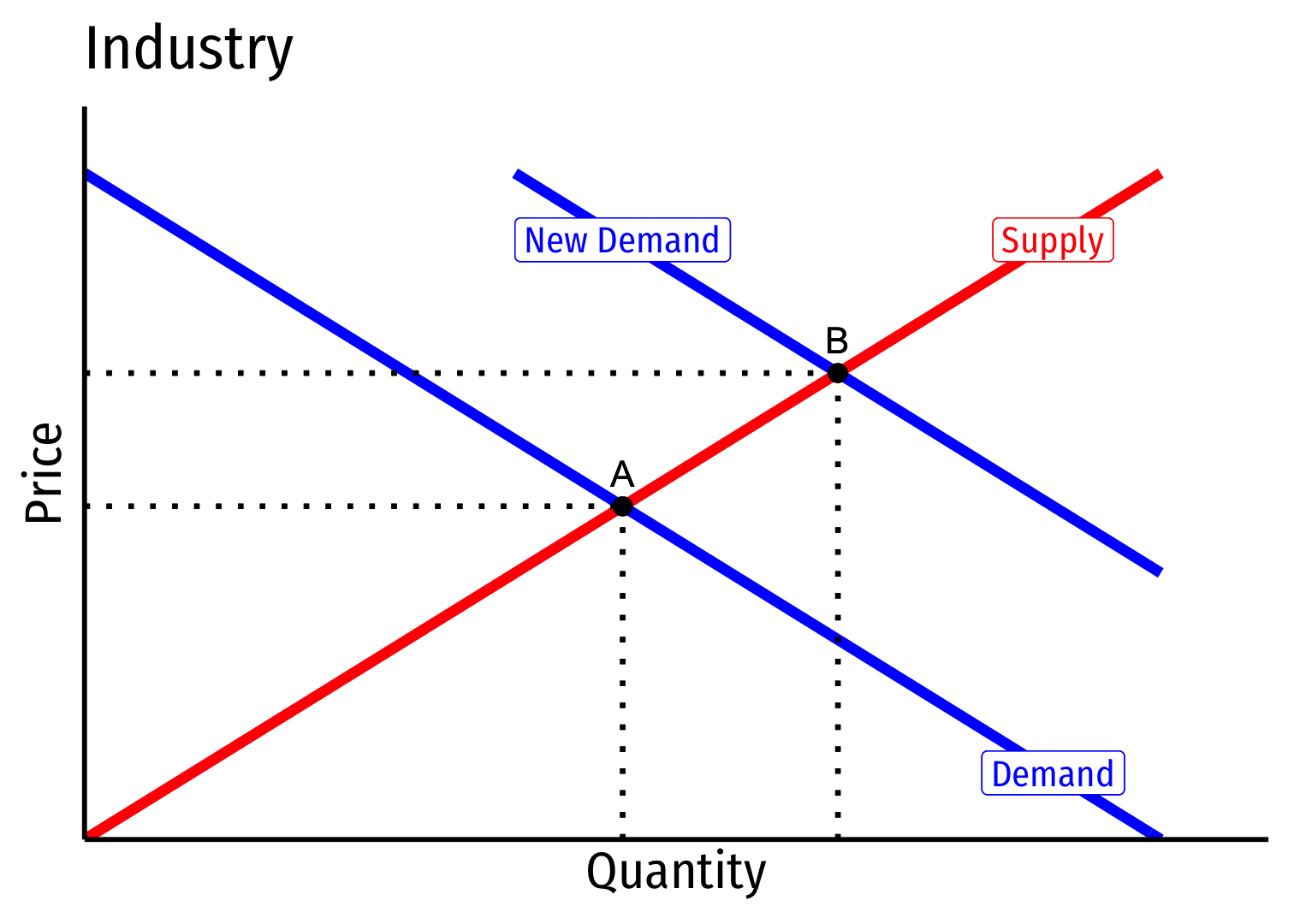
  • Exogenous increase in market demand

Constant Cost Industry (No External Economies) IV

  • Short run (A→B): industry reaches new equilibrium

  • Firms charge higher p∗, produce more q∗, earn π

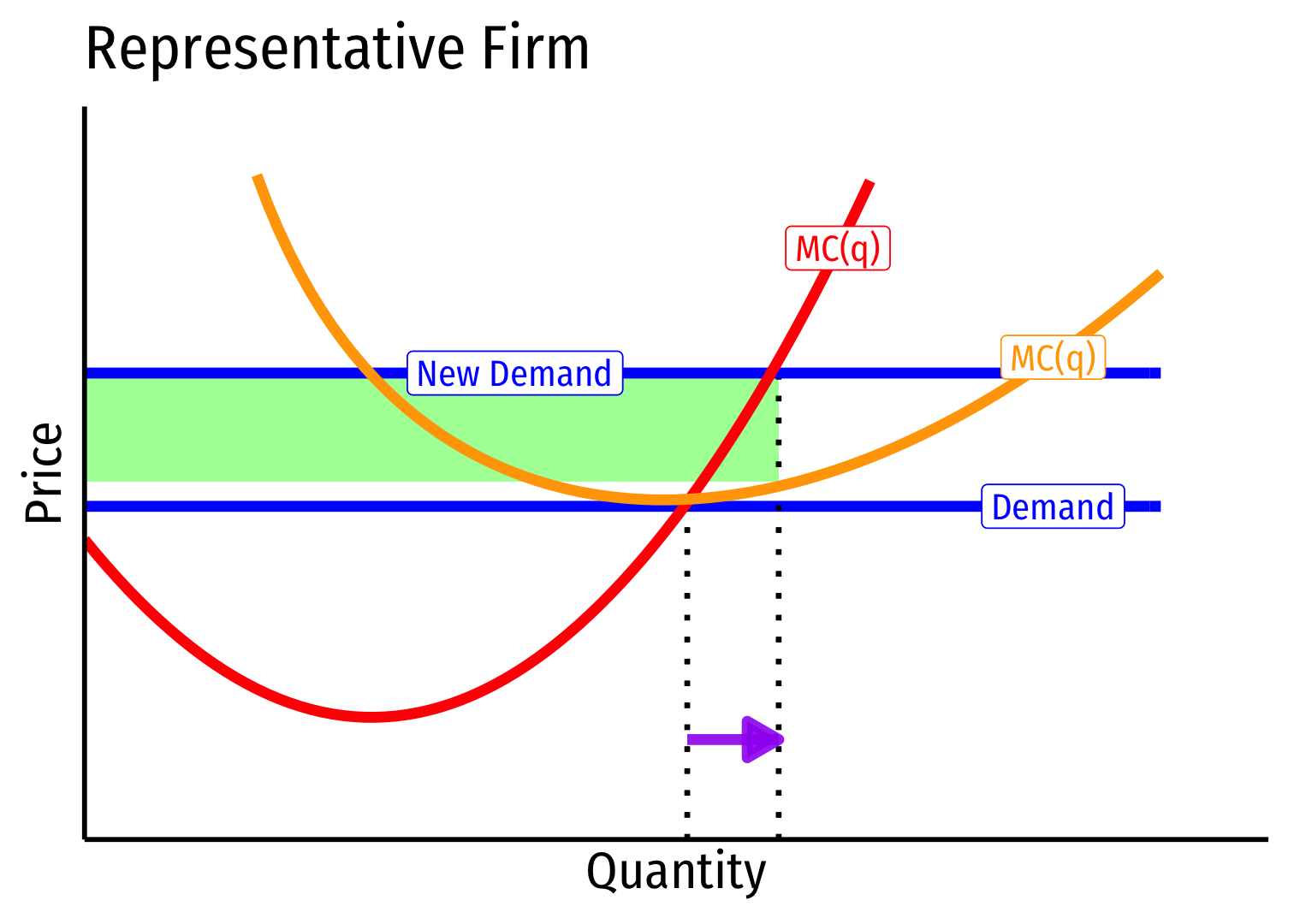
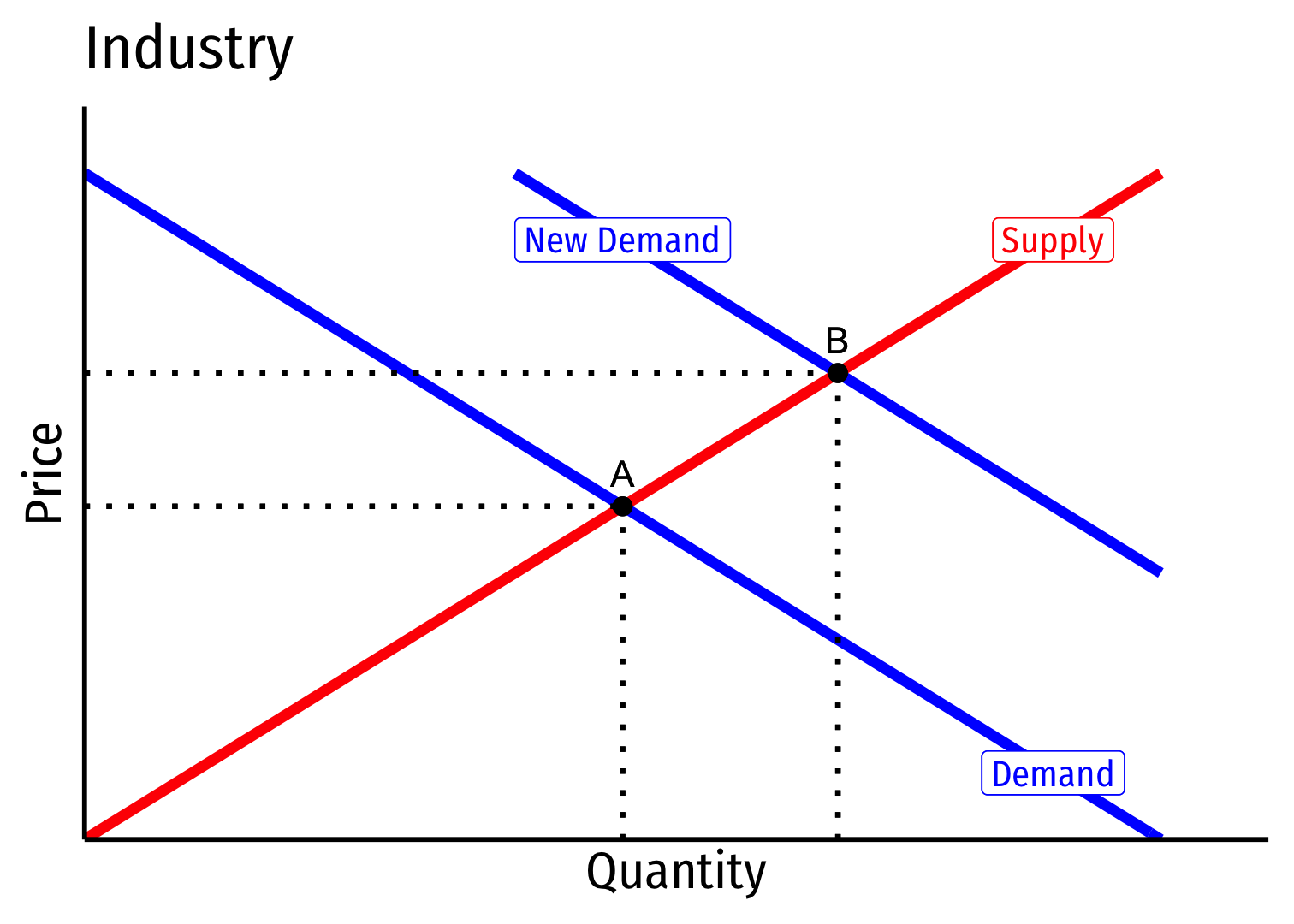
Constant Cost Industry (No External Economies) V

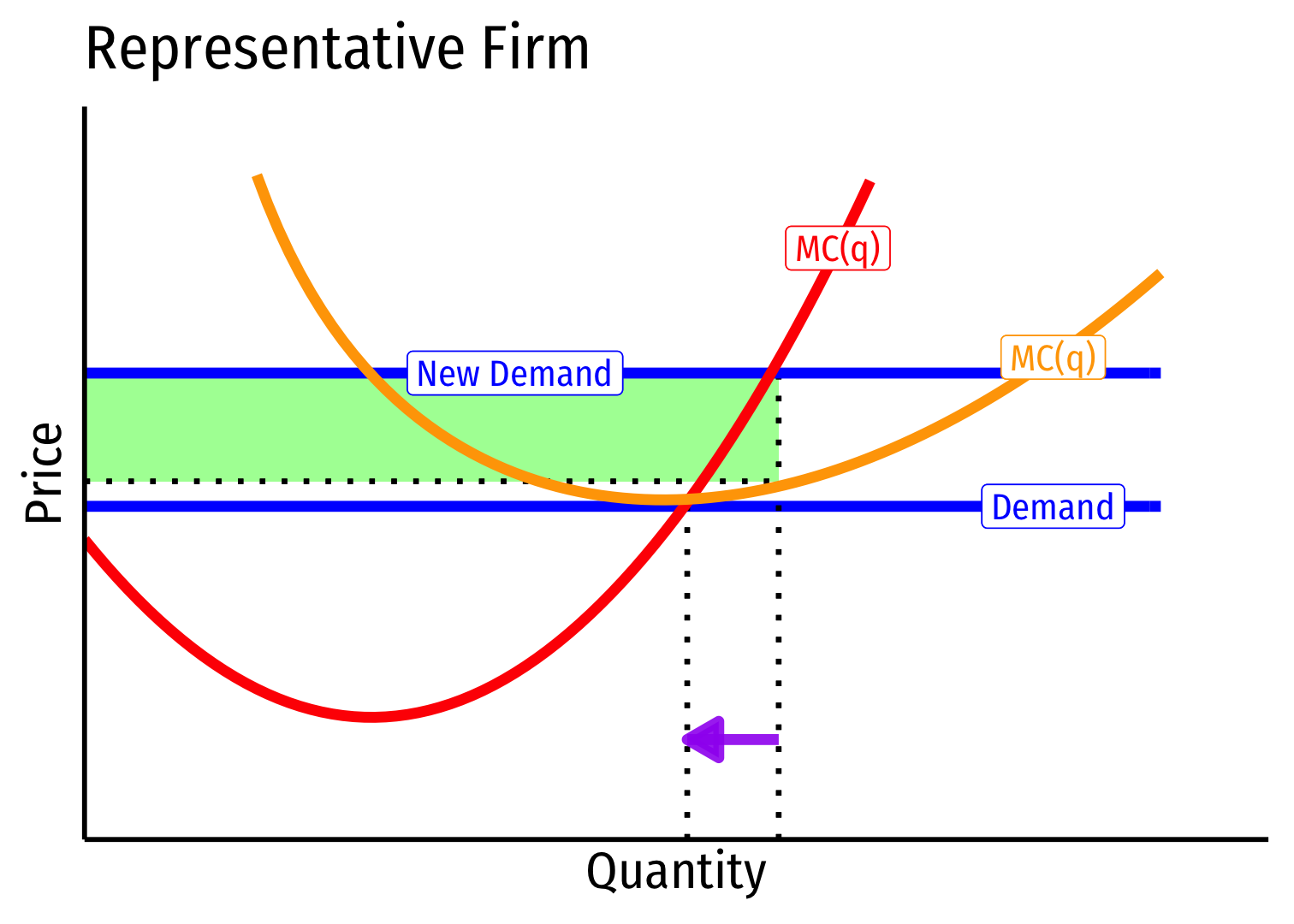
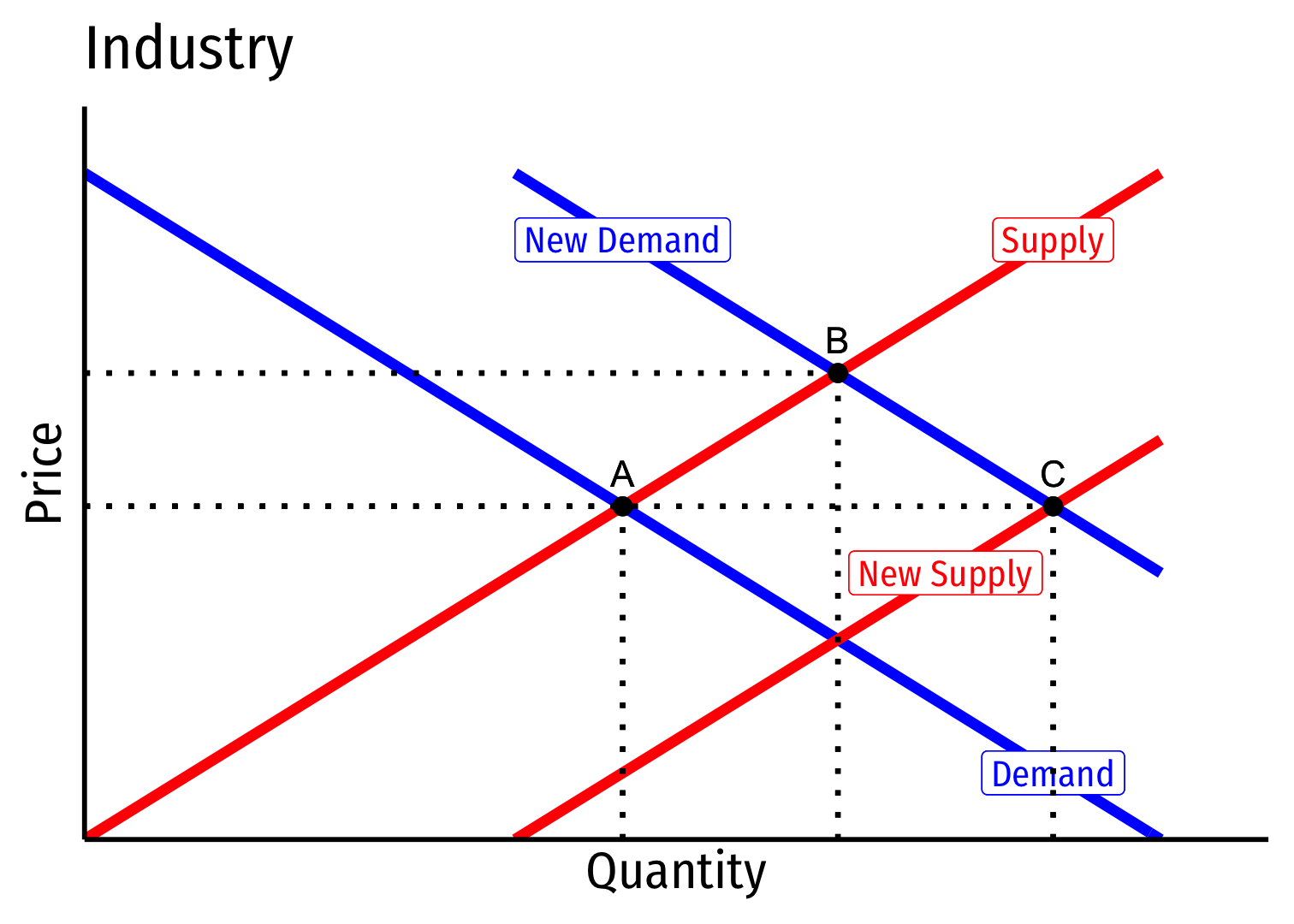
  • Long run (B→C): profit attracts entry ⟹ industry supply increases

  • No change in costs to firms in industry, firms enter until π=0 at p=AC(q)

  • Firms must charge original p∗, return to original q∗, earn π=0

Constant Cost Industry (No External Economies) VI

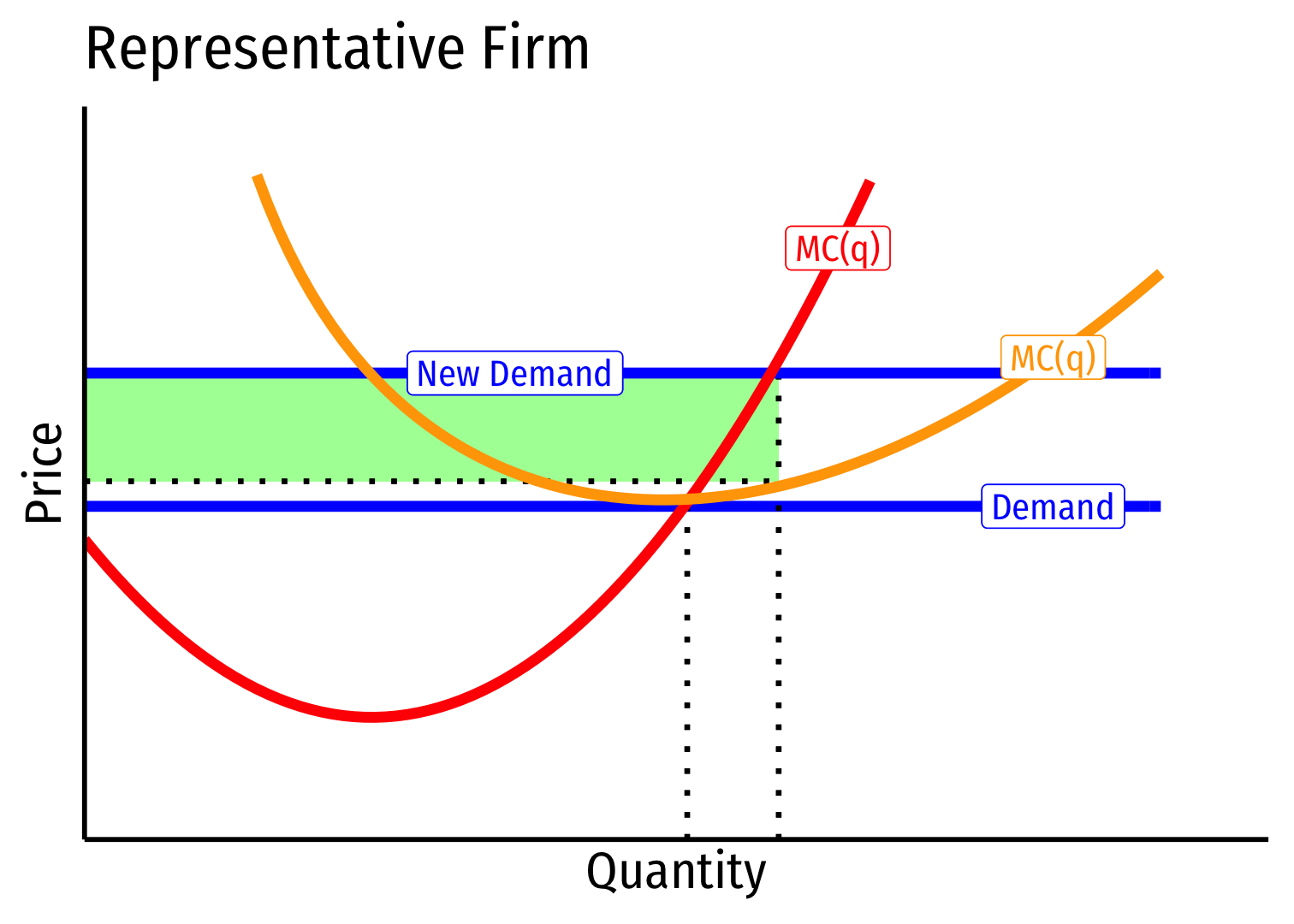
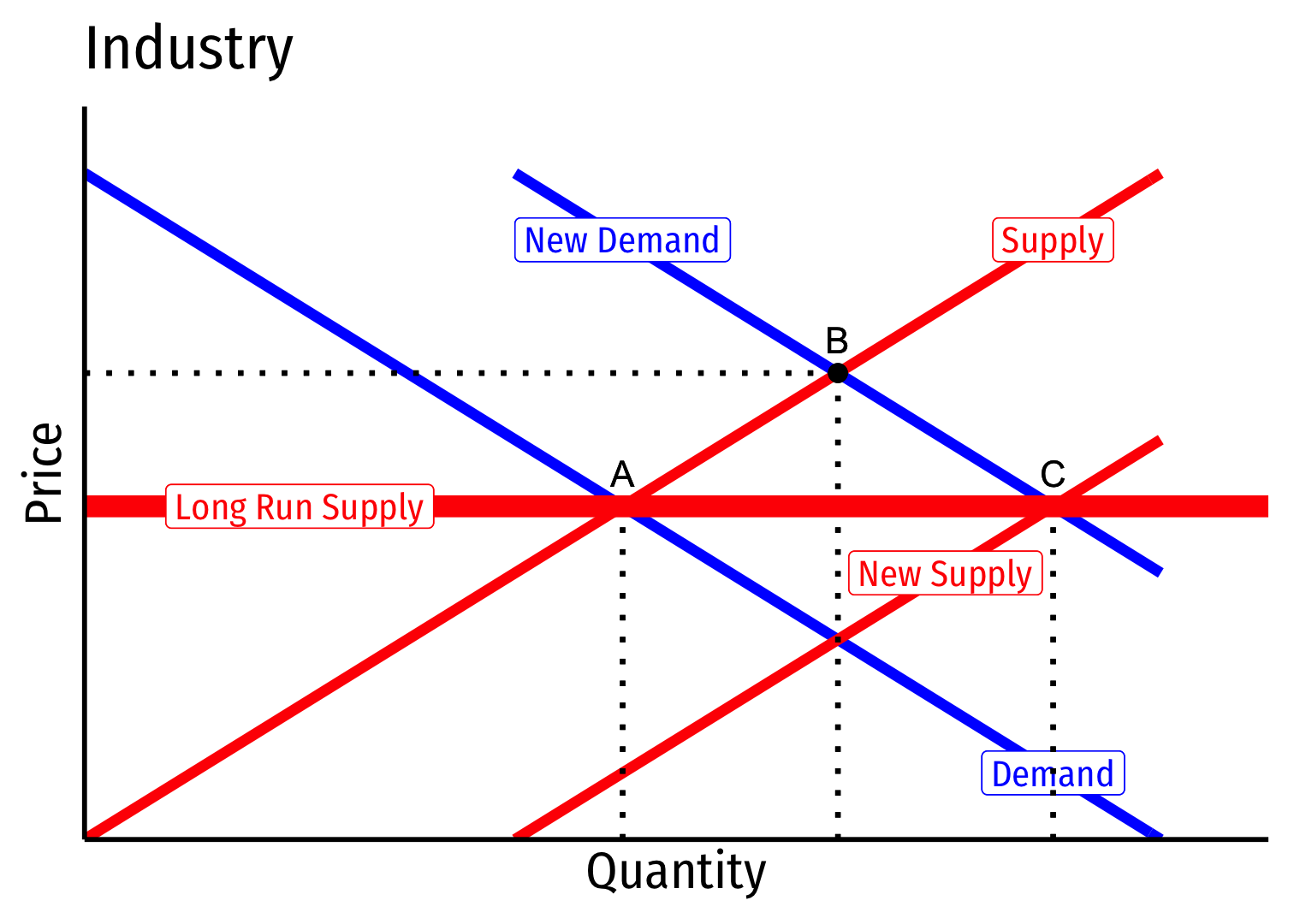
  • Long Run Industry Supply is perfectly elastic

Increasing Cost Industry (External Diseconomies) I

  • Increasing cost industry has external _dis_economies, costs rise for all firms in the industry as industry output increases (firms enter & incumbents produce more)

  • An upward sloping long-run industry supply curve!

  • Determinants:

    • Finding more resources in harder-to-reach places
    • Diminishing marginal products
    • Greater complexity and administrative costs at larger scales

  • Examples: oil, mining, particle physics

Increasing Cost Industry (External Diseconomies) II

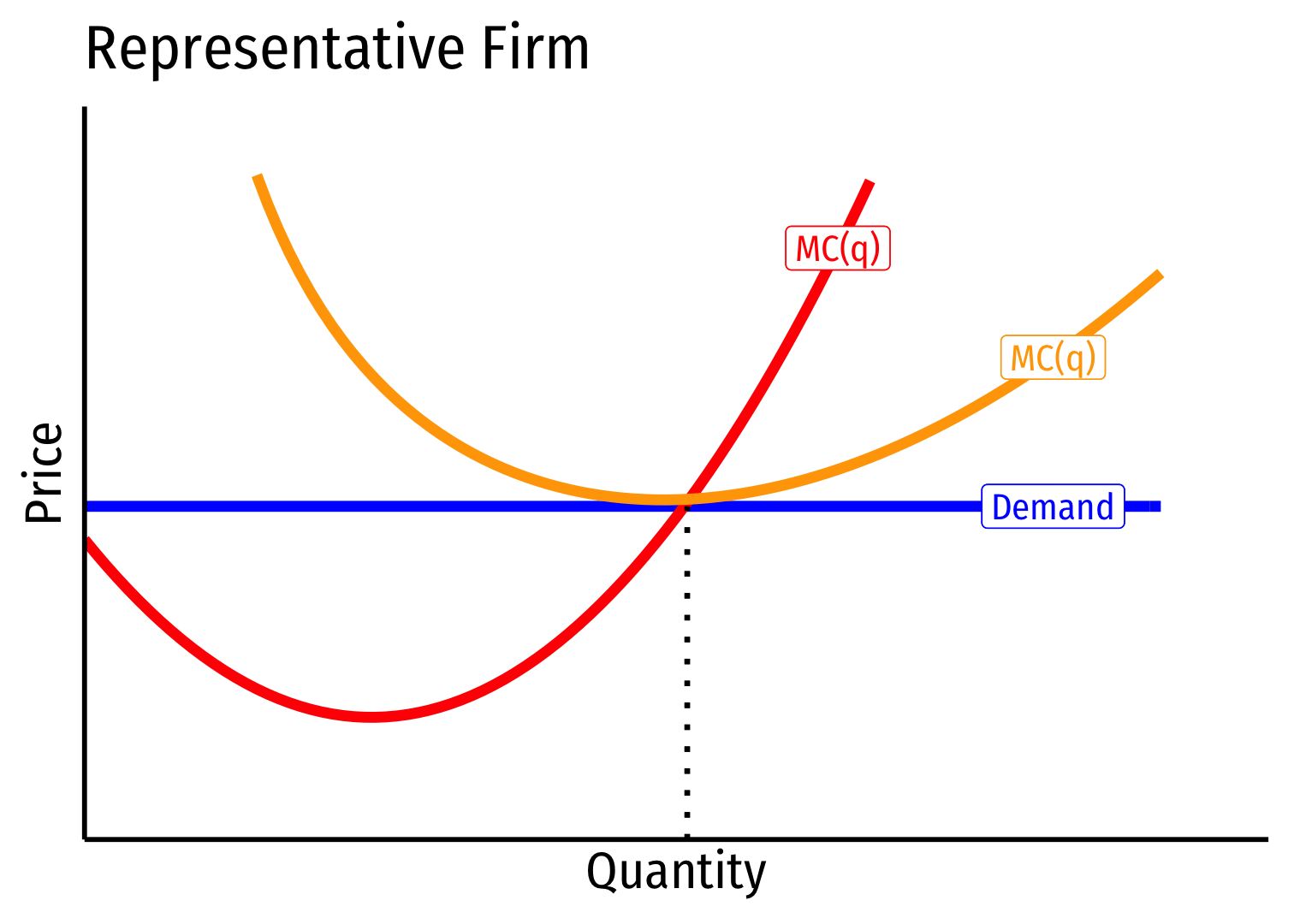
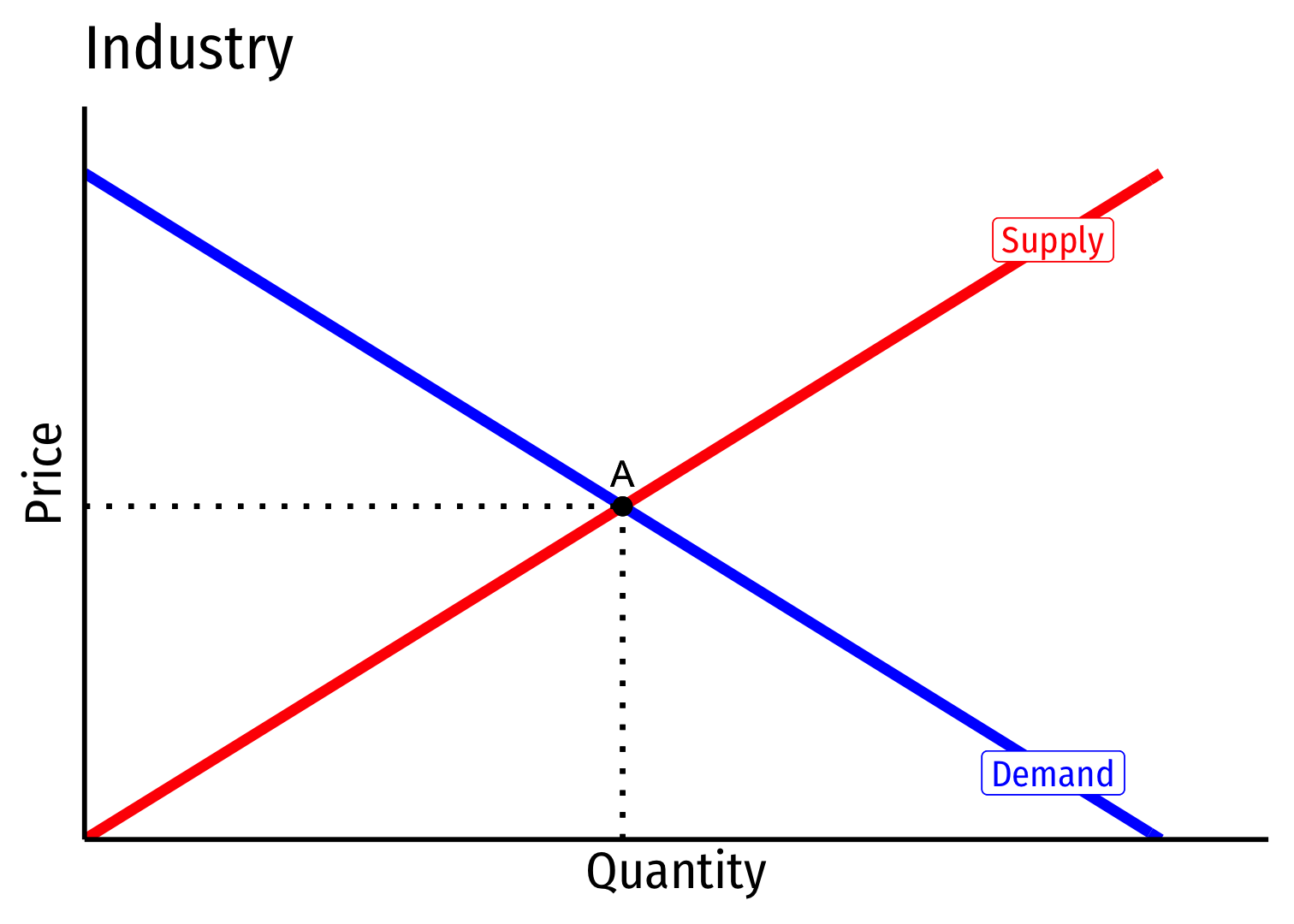
  • Industry equilibrium: firms earning normal π=0,p=MC(q)=AC(q)

Increasing Cost Industry (External Diseconomies) III

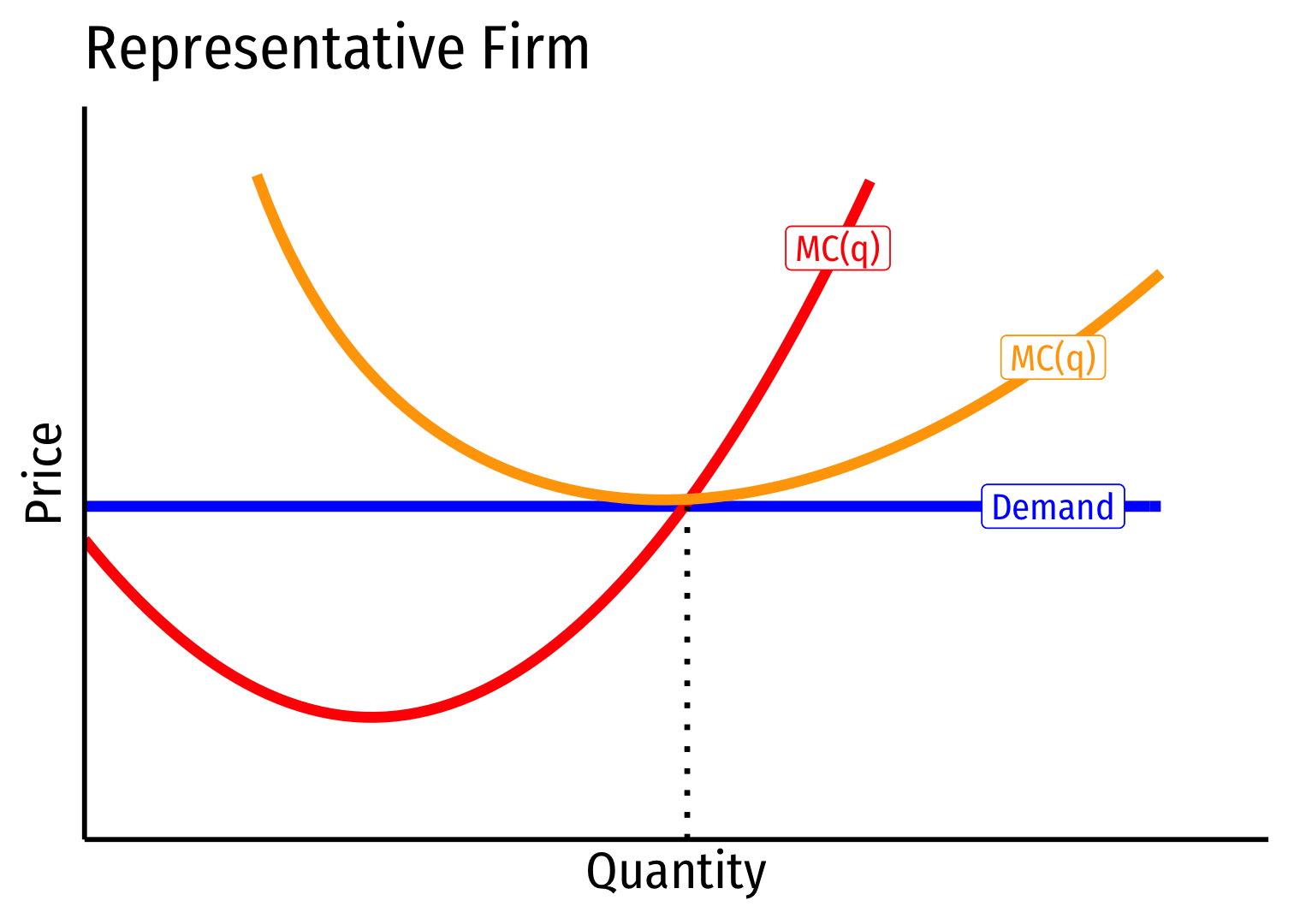
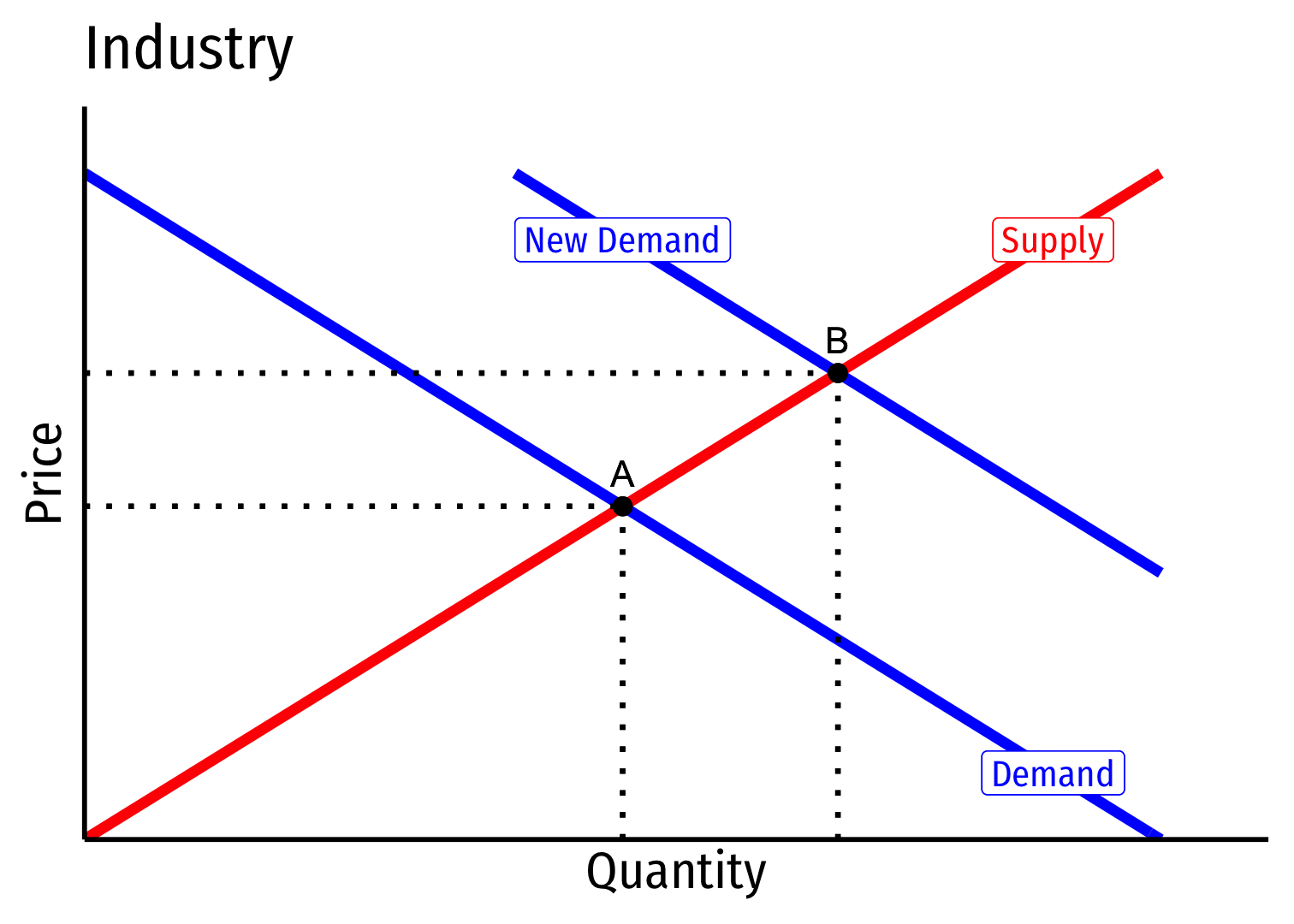
  • Industry equilibrium: firms earning normal π=0,p=MC(q)=AC(q)

  • Exogenous increase in market demand

Increasing Cost Industry (External Diseconomies) IV

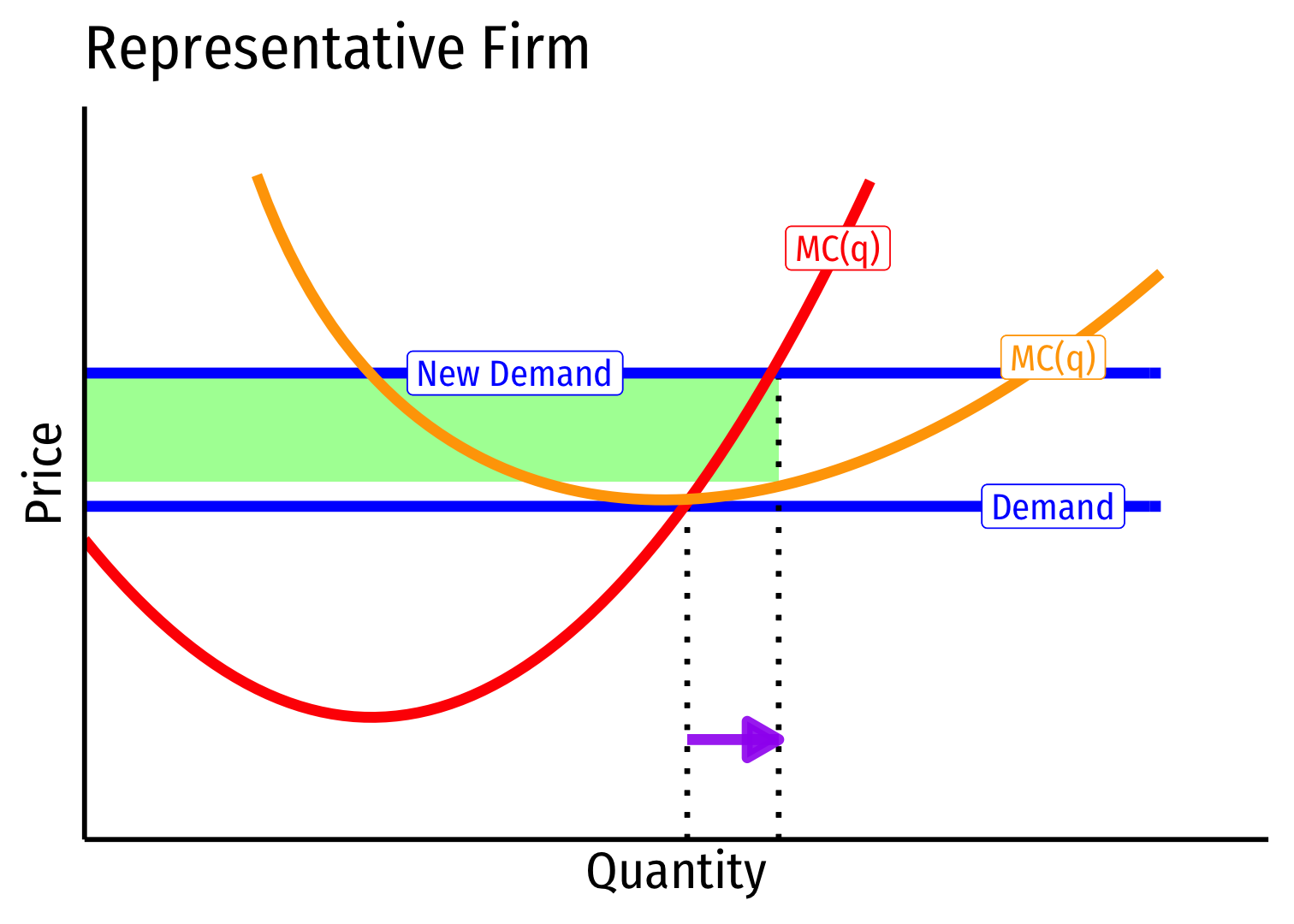
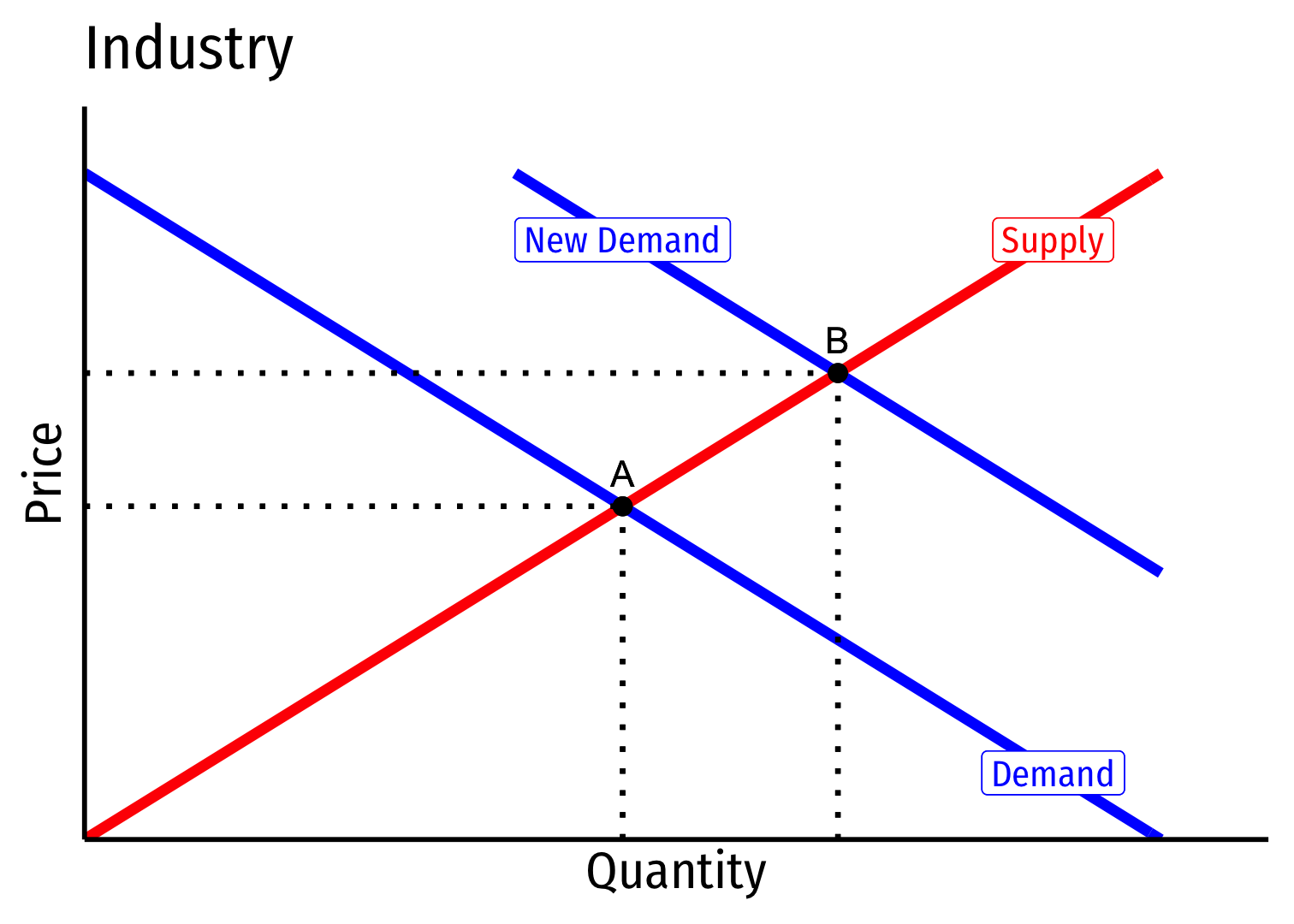
  • Short run (A→B): industry reaches new equilibrium

  • Firms charge higher p∗, produce more q∗, earn π

Increasing Cost Industry (External Diseconomies) V

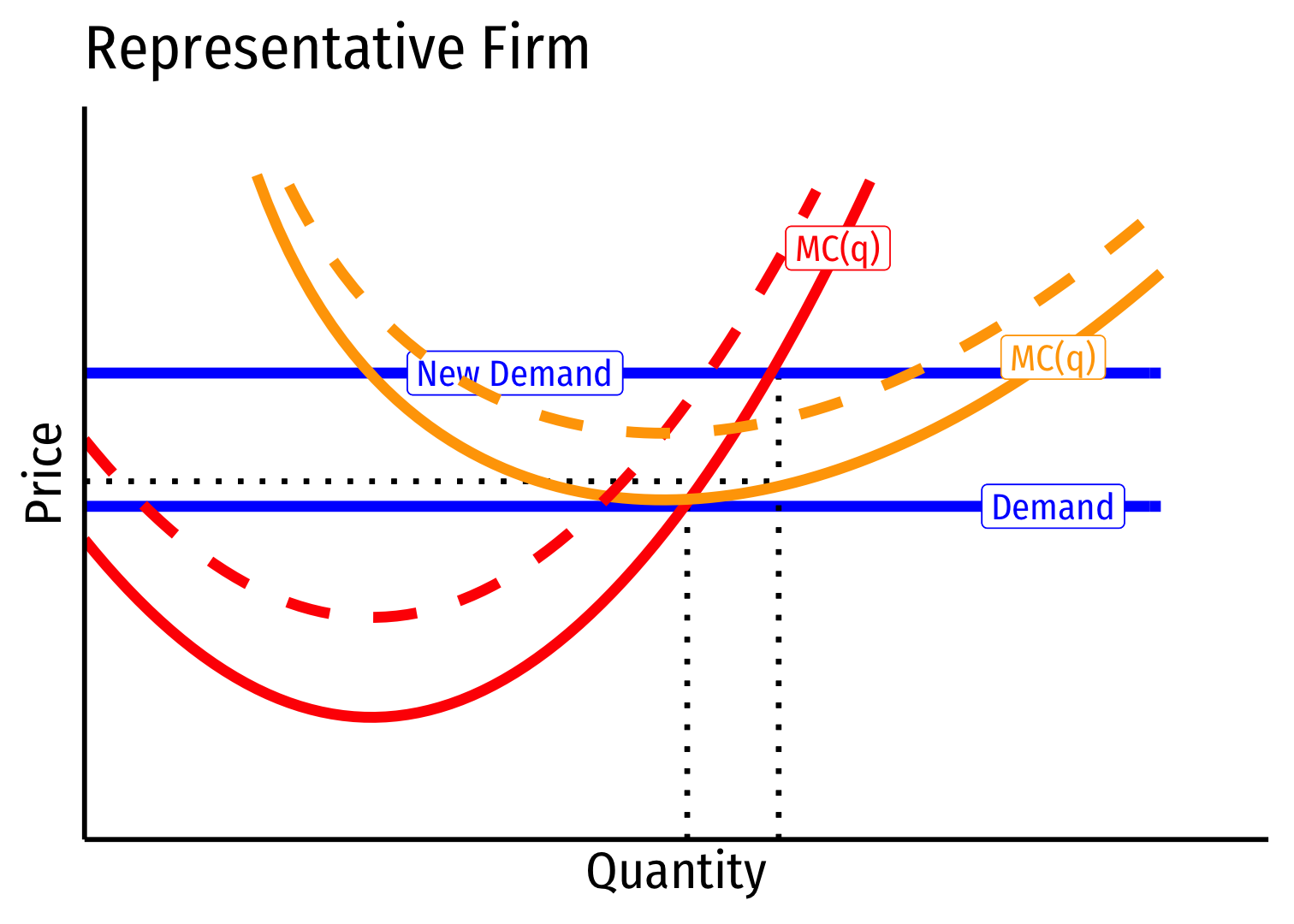
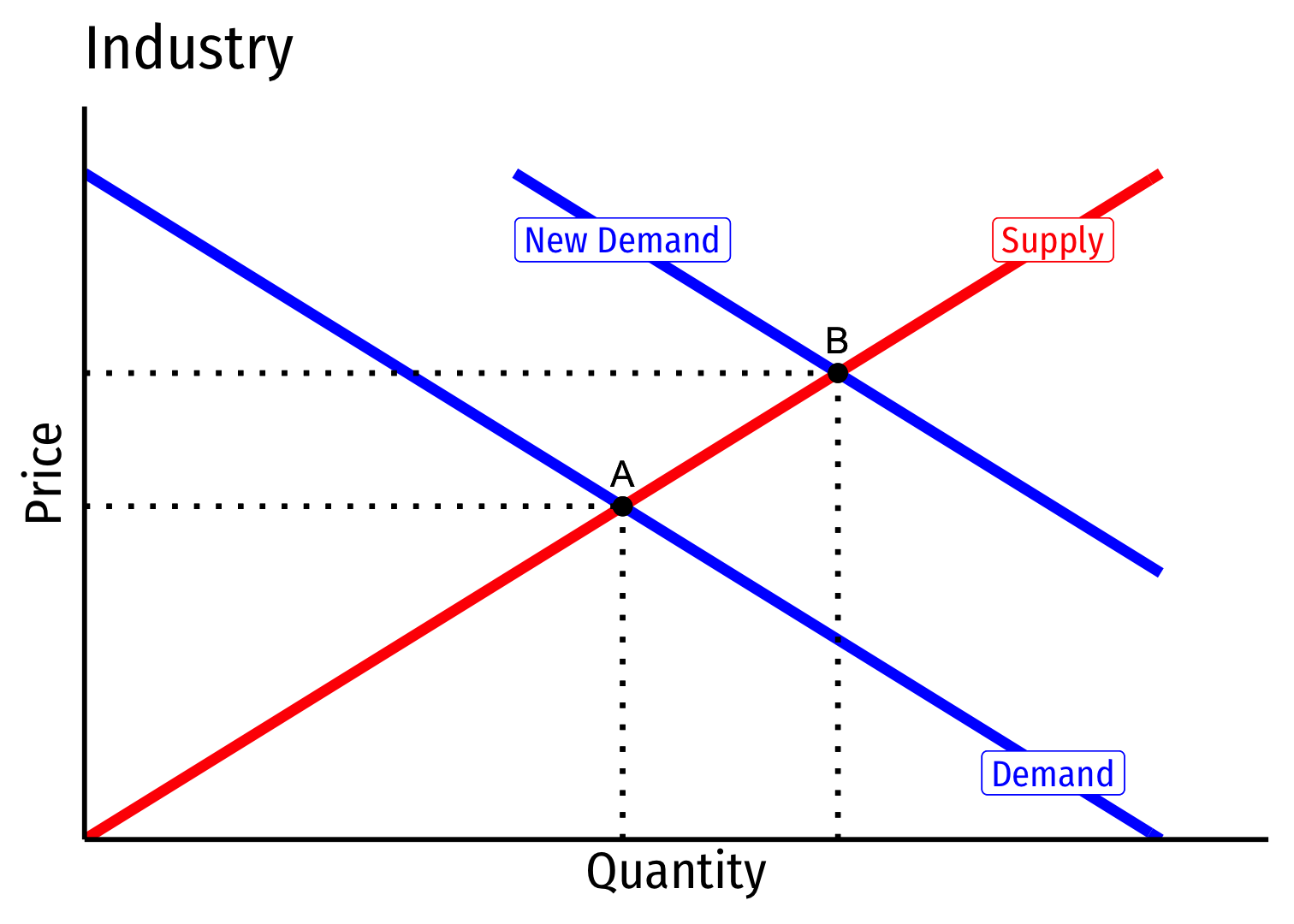
  • Long run: profit attracts entry ⟹ industry supply will increase

  • But more production increases costs (MC,AC) for all firms in industry

Increasing Cost Industry (External Diseconomies) VI

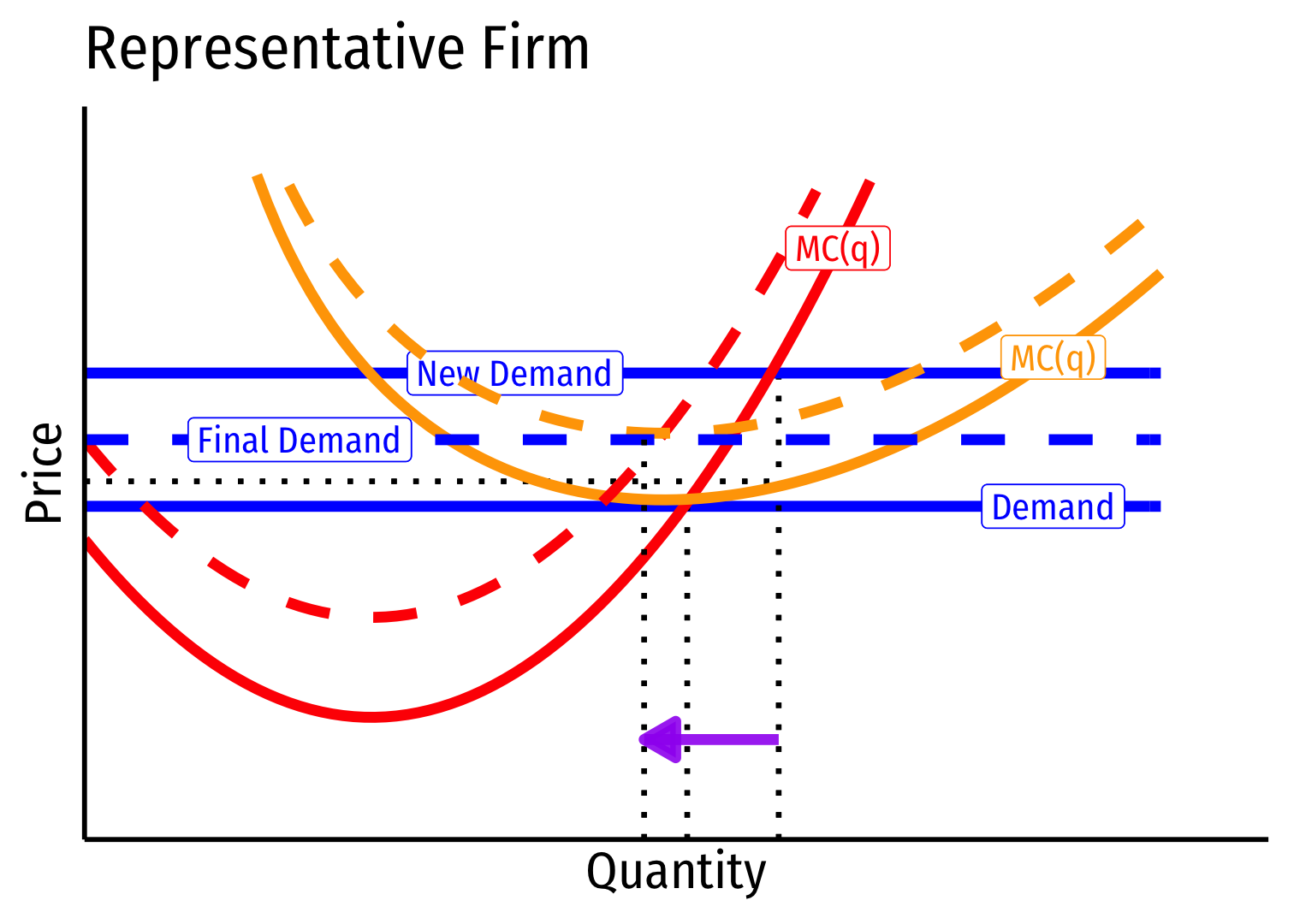
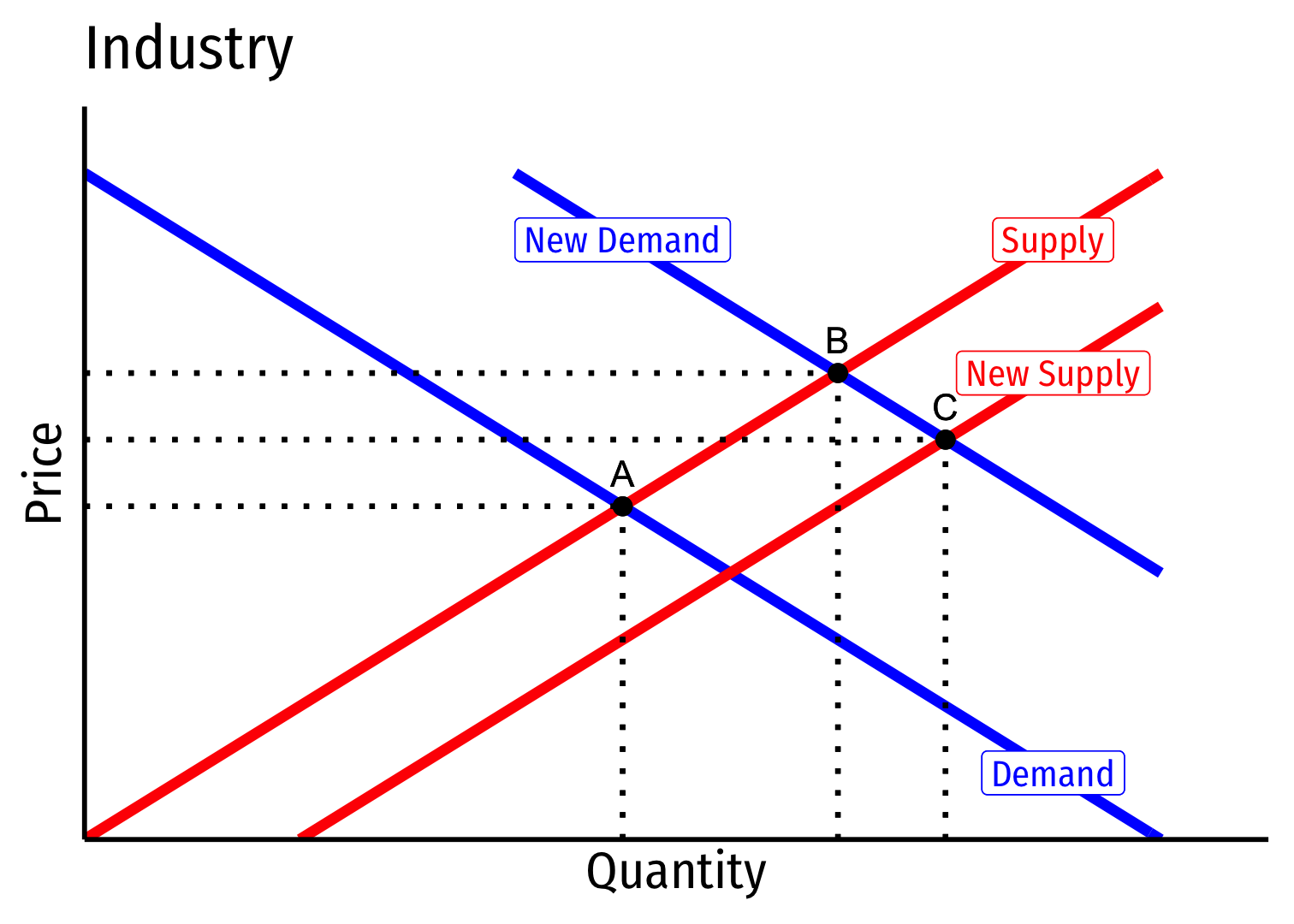
  • Long run (B→C): firms enter until π=0 at p=AC(q)

  • Firms charge higher p∗, producer lower q∗, earn π=0

Increasing Cost Industry (External Diseconomies) VII

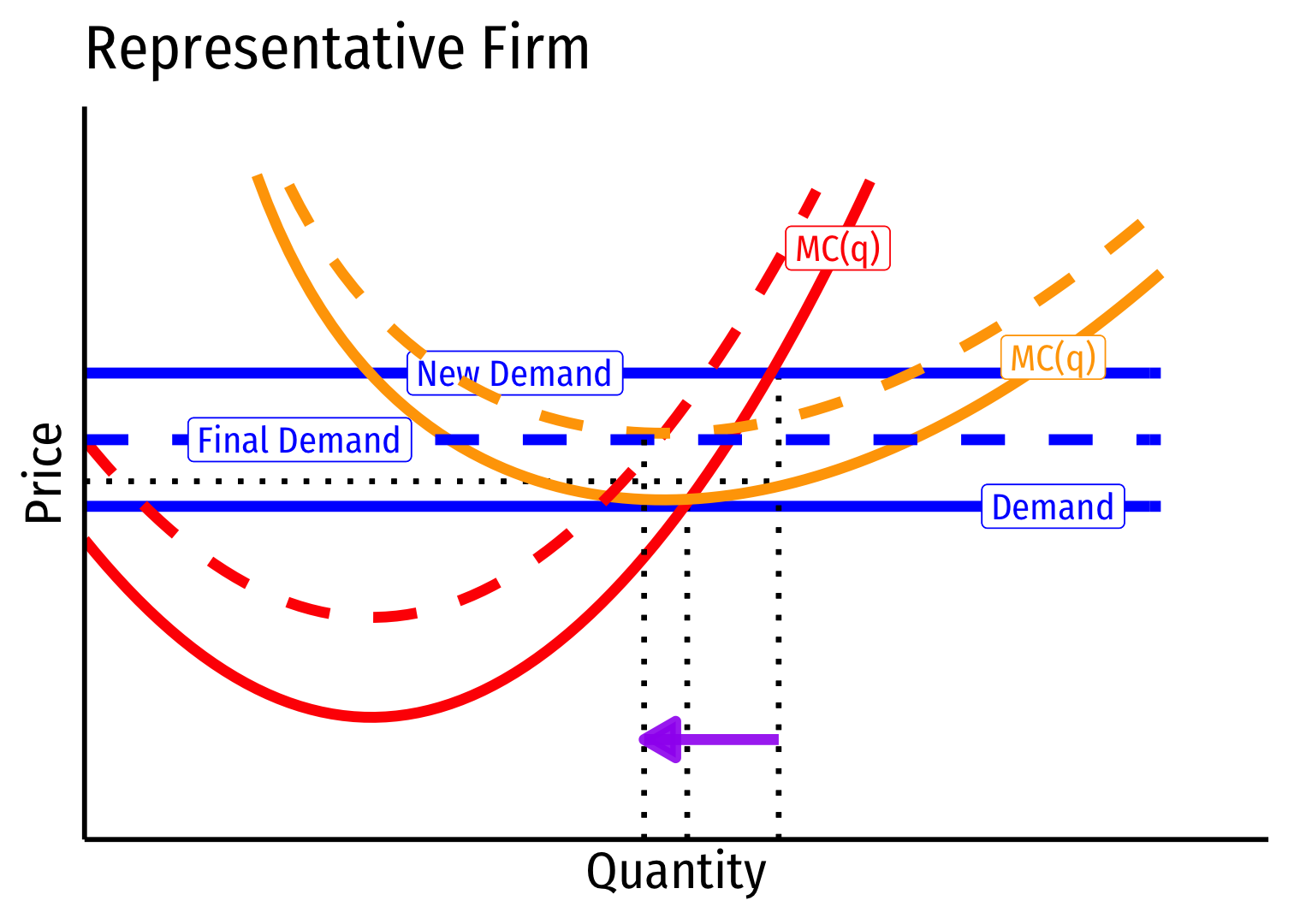
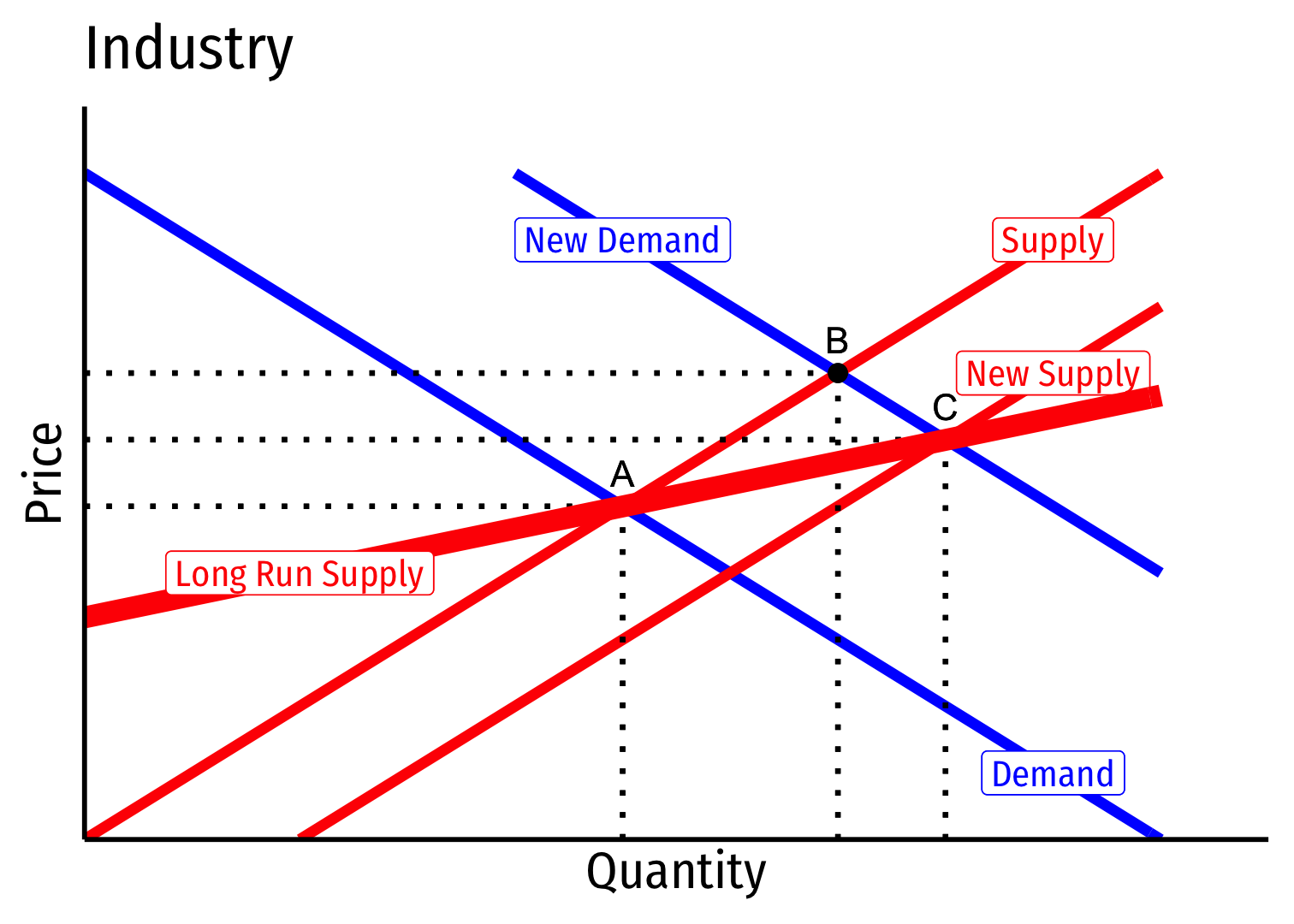
  • Long run industry supply curve is upward sloping

Decreasing Cost Industry (External Economies) I

  • Decreasing cost industry has external economies, costs fall for all firms in the industry as industry output increases (firms enter & incumbents produce more)

  • A downward sloping long-run industry supply curve!

  • Determinants:

    • High fixed costs, low marginal costs
    • Economies of scale

  • Examples: geographic clusters, public utilities, infrastructure, entertainment

  • Tends towards "natural" monopoly

Decreasing Cost Industry (External Economies) II

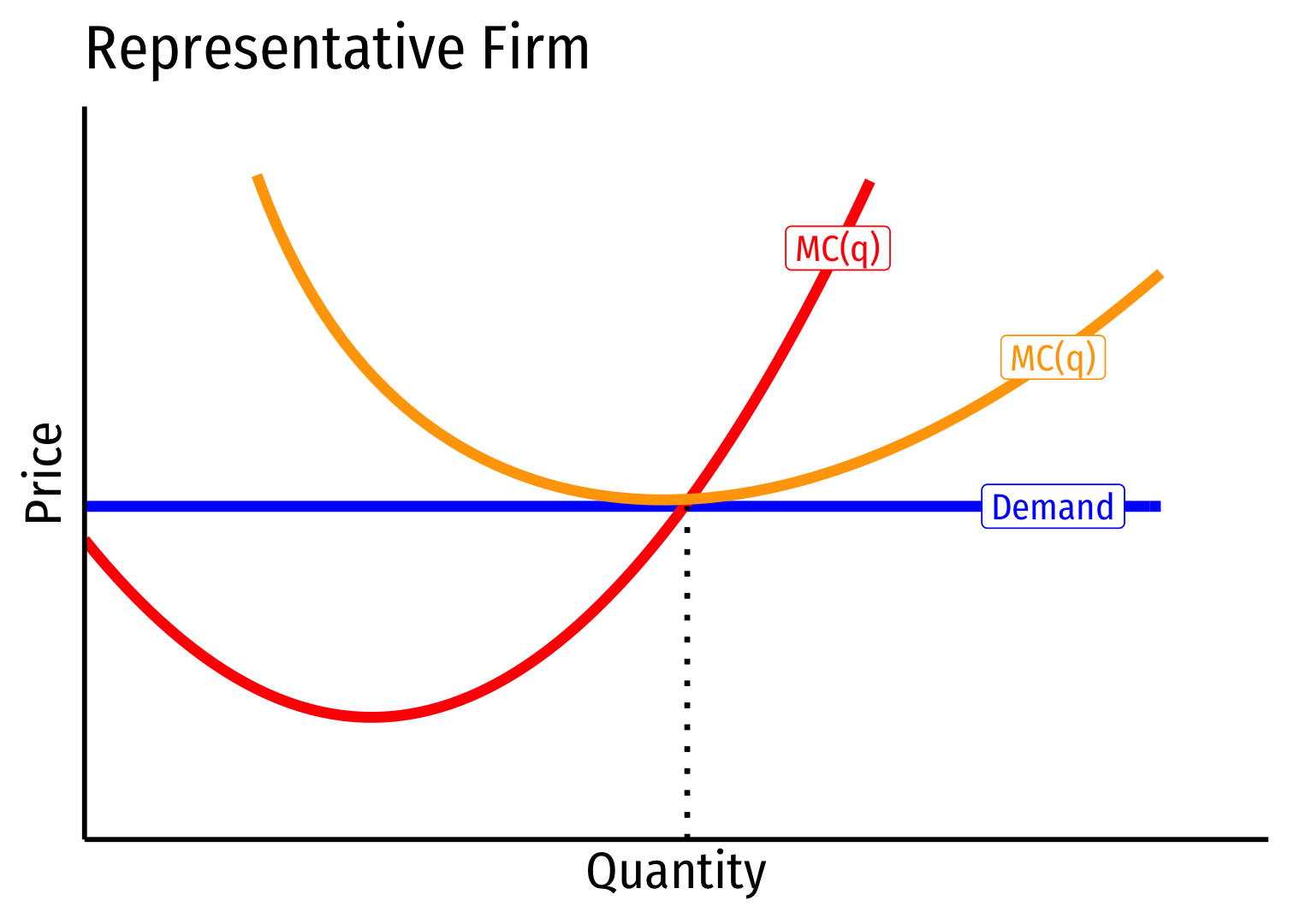
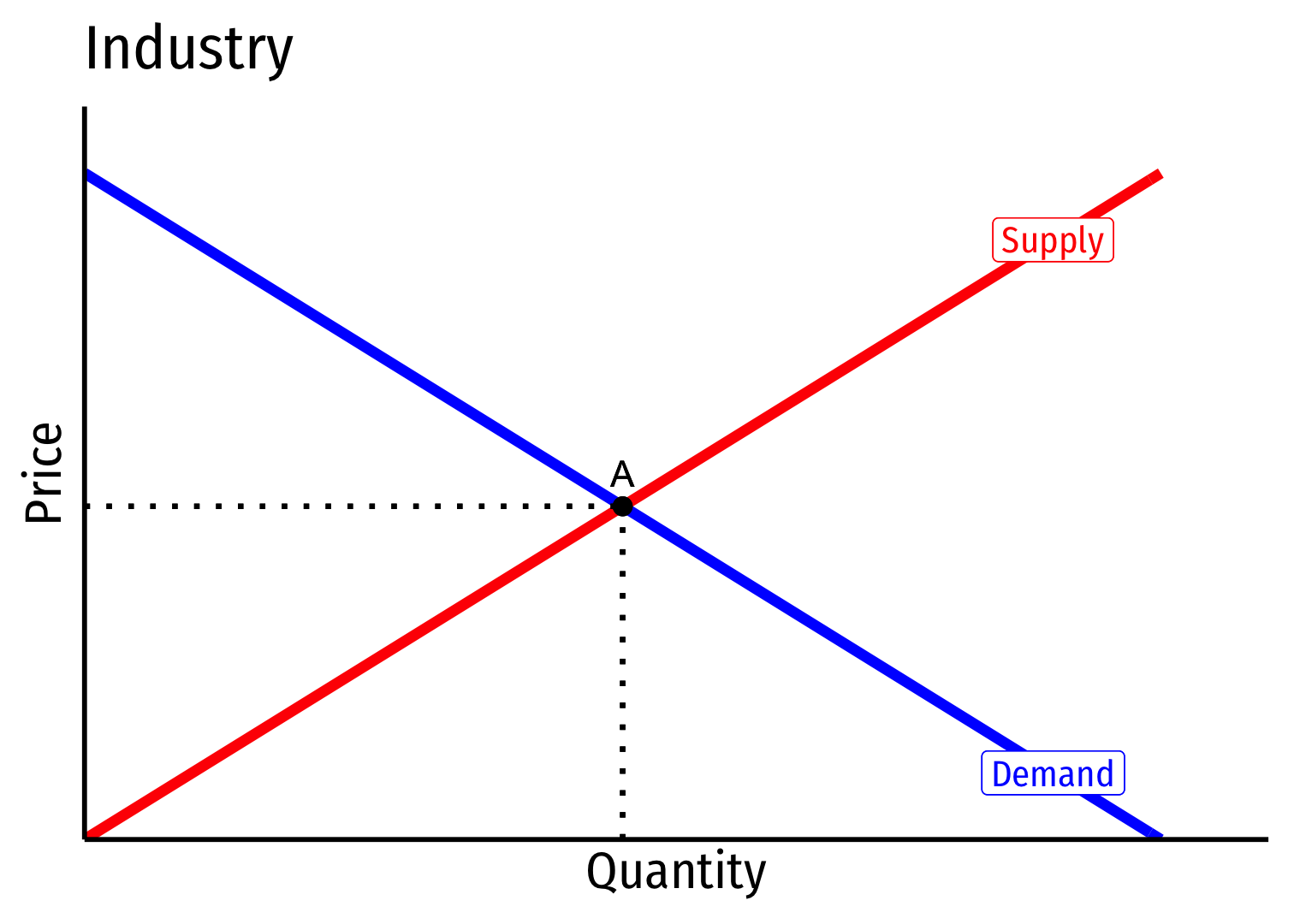
  • Industry equilibrium: firms earning normal π=0,p=MC(q)=AC(q)

Decreasing Cost Industry (External Economies) III

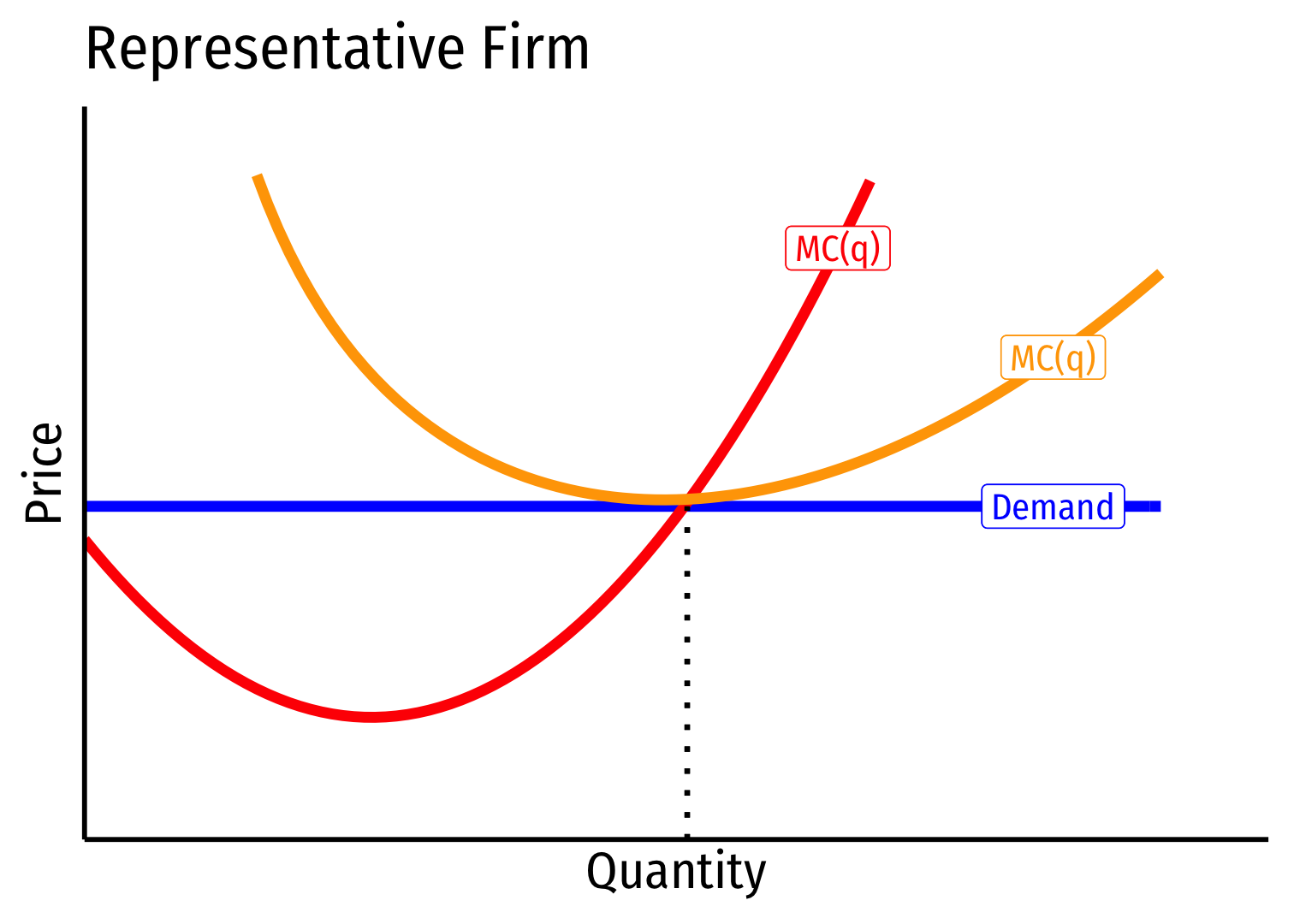
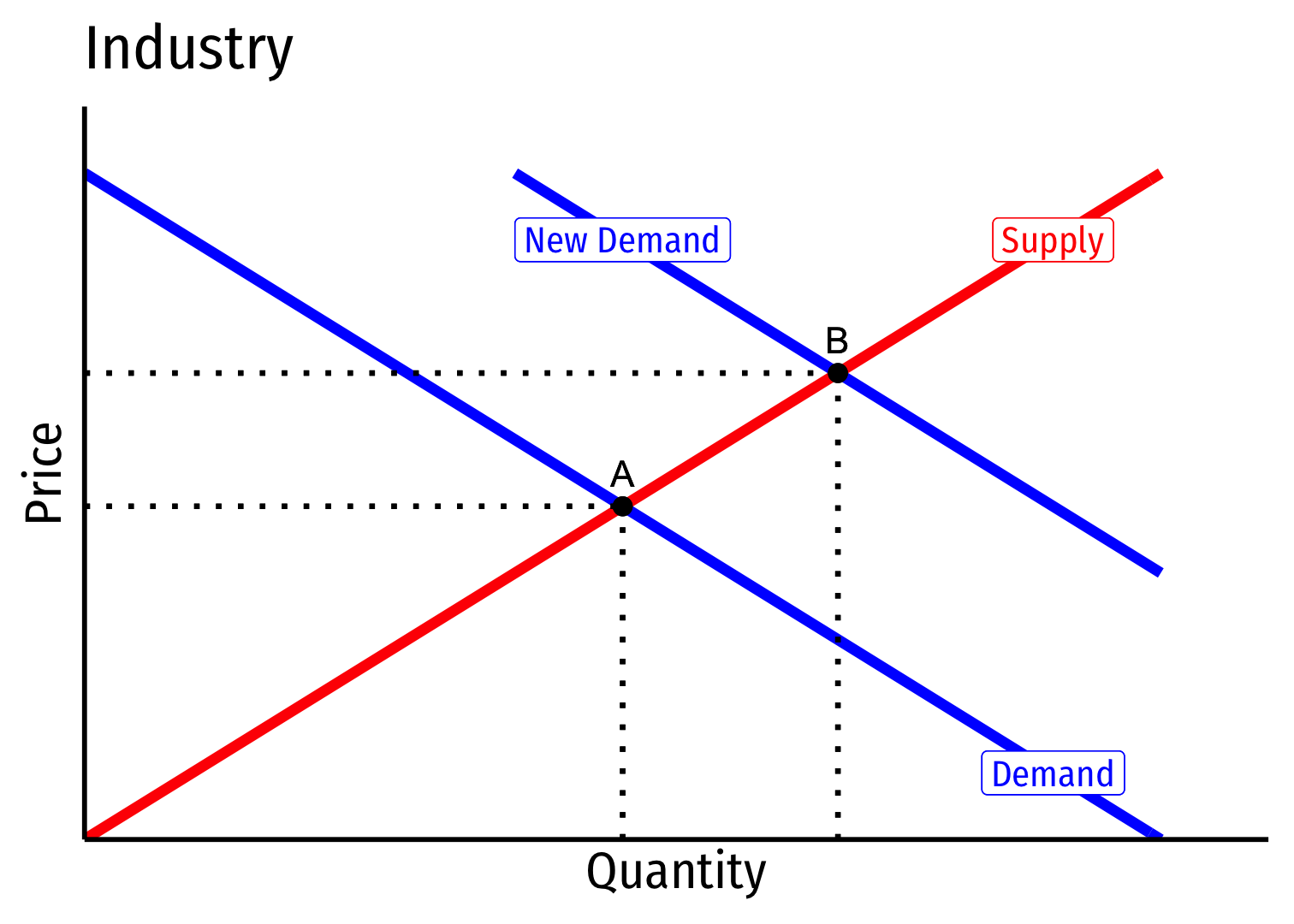
  • Industry equilibrium: firms earning normal π=0,p=MC(q)=AC(q)

  • Exogenous increase in market demand

Decreasing Cost Industry (External Economies) IV

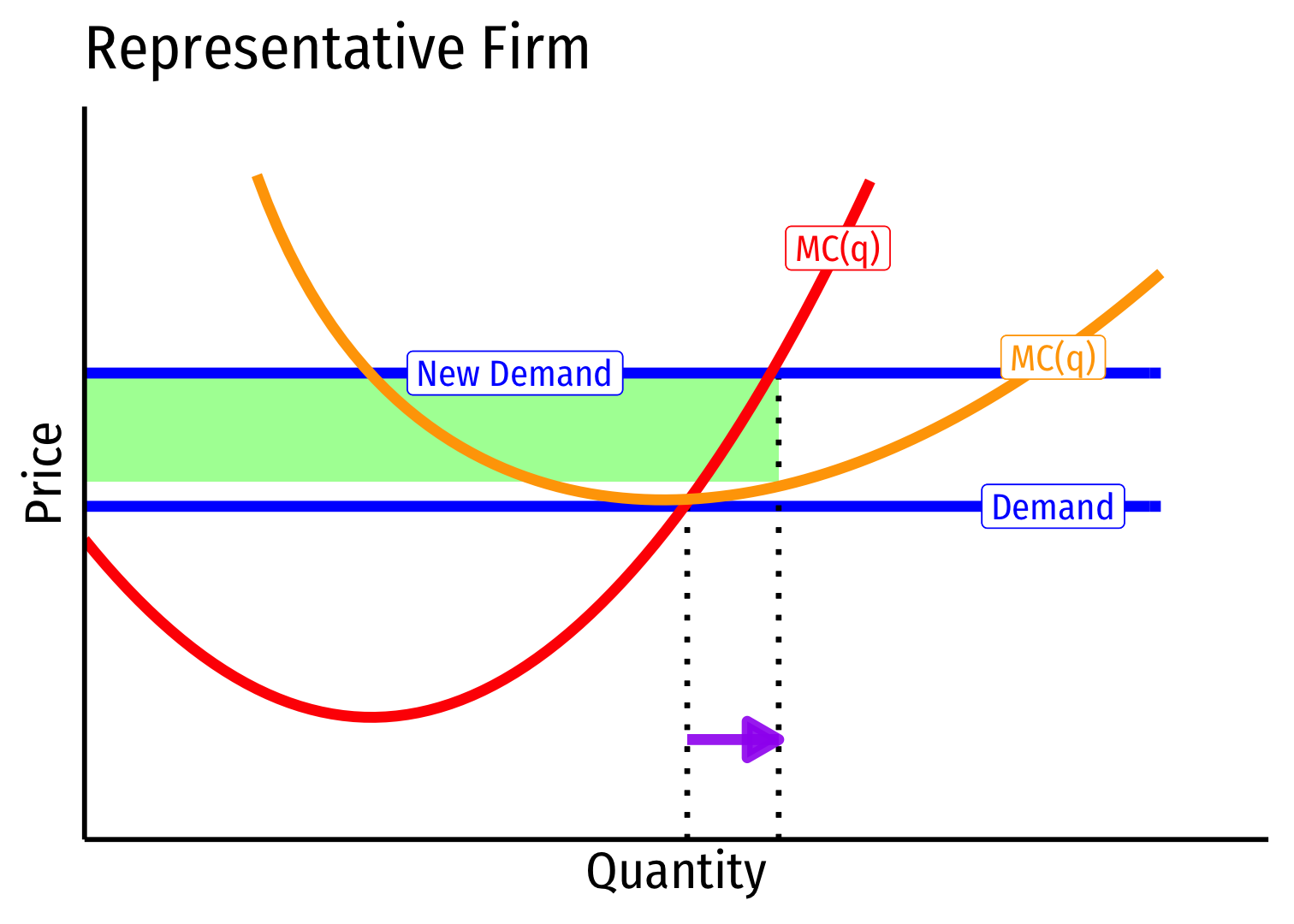
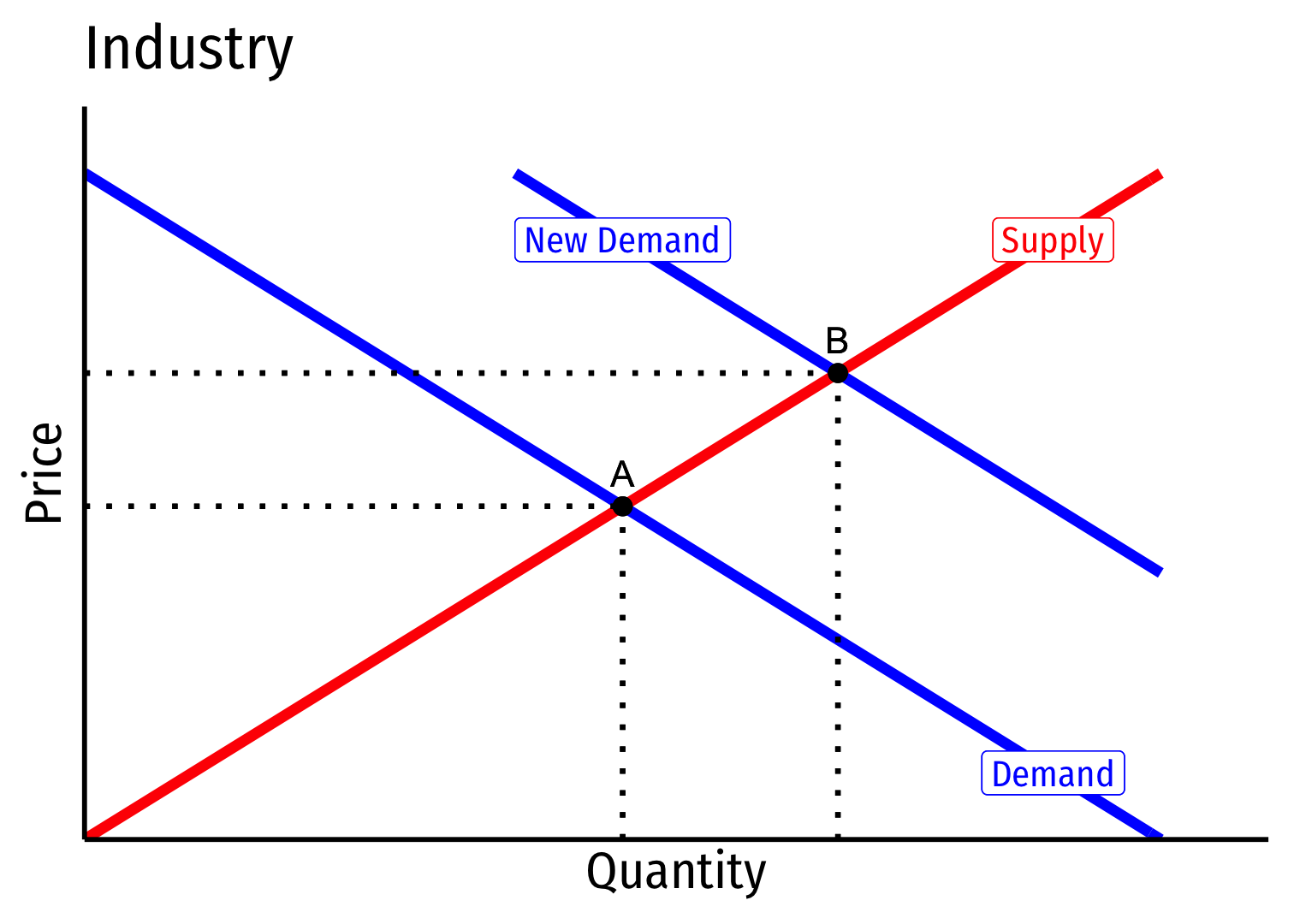
  • Short run (A→B): industry reaches new equilibrium

  • Firms charge higher p∗, produce more q∗, earn π

Decreasing Cost Industry (External Economies) V

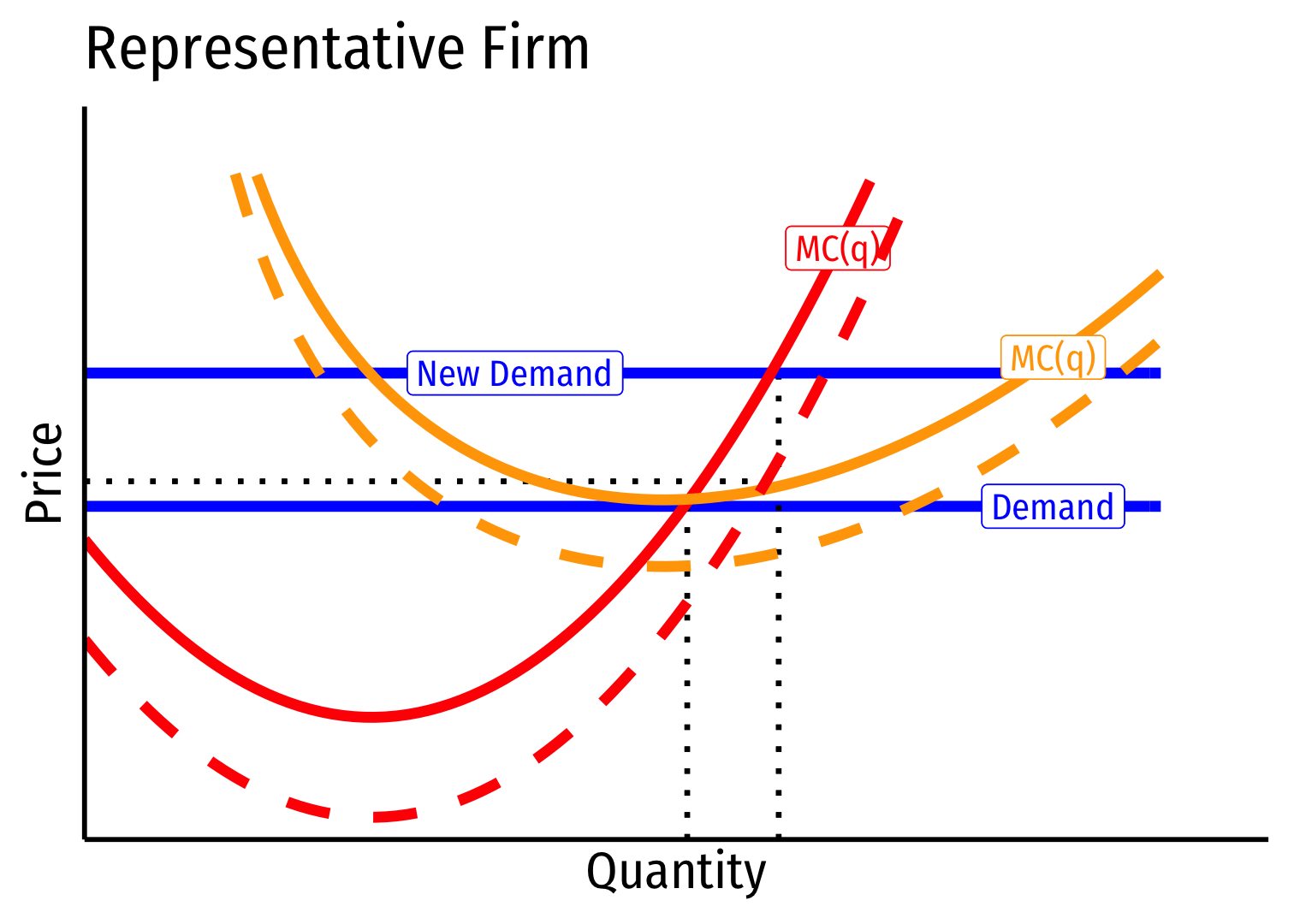
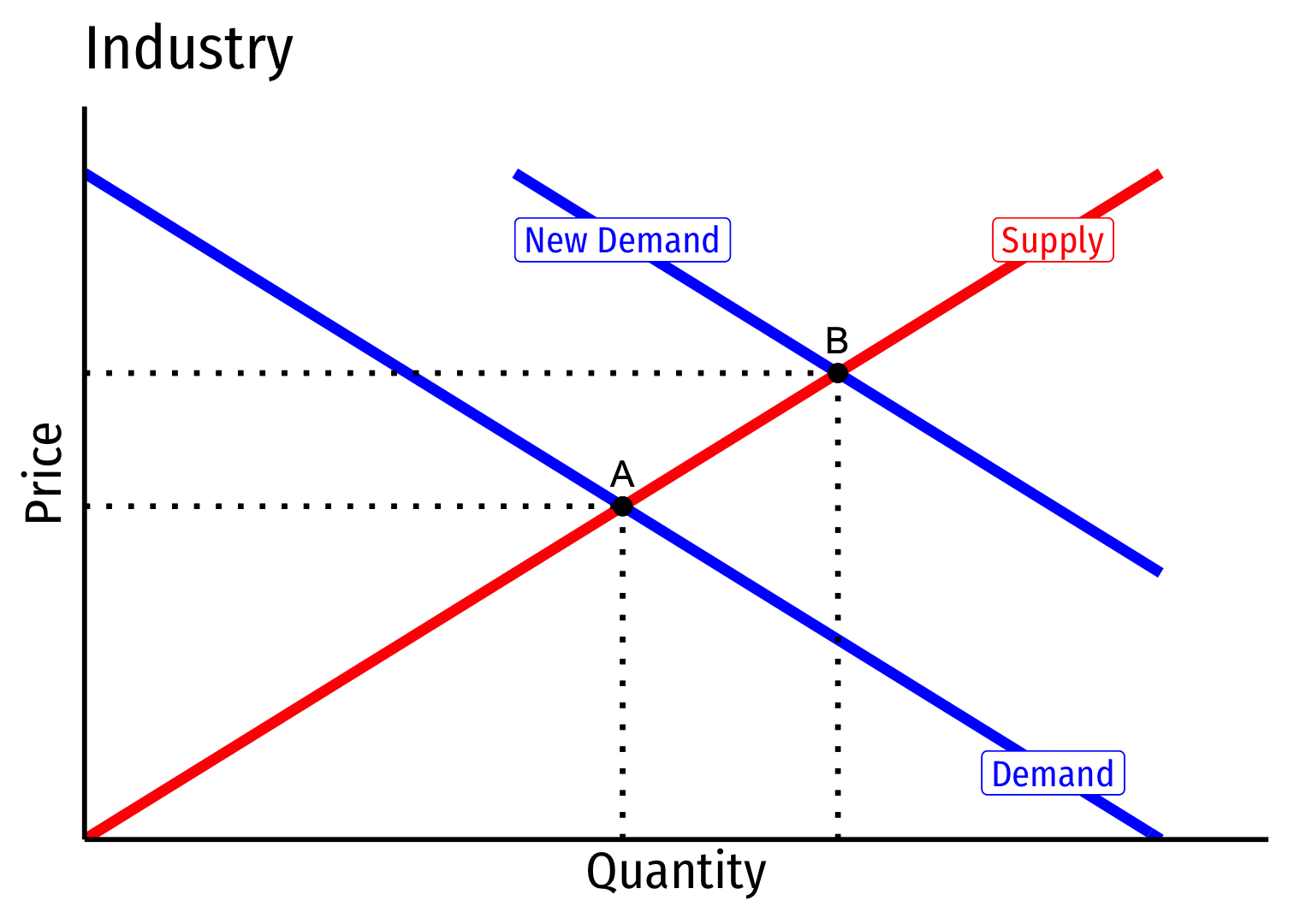
  • Long run: profit attracts entry ⟹ industry supply will increase

  • But more production lowers costs (MC,AC) for all firms in industry

Decreasing Cost Industry (External Economies) VI

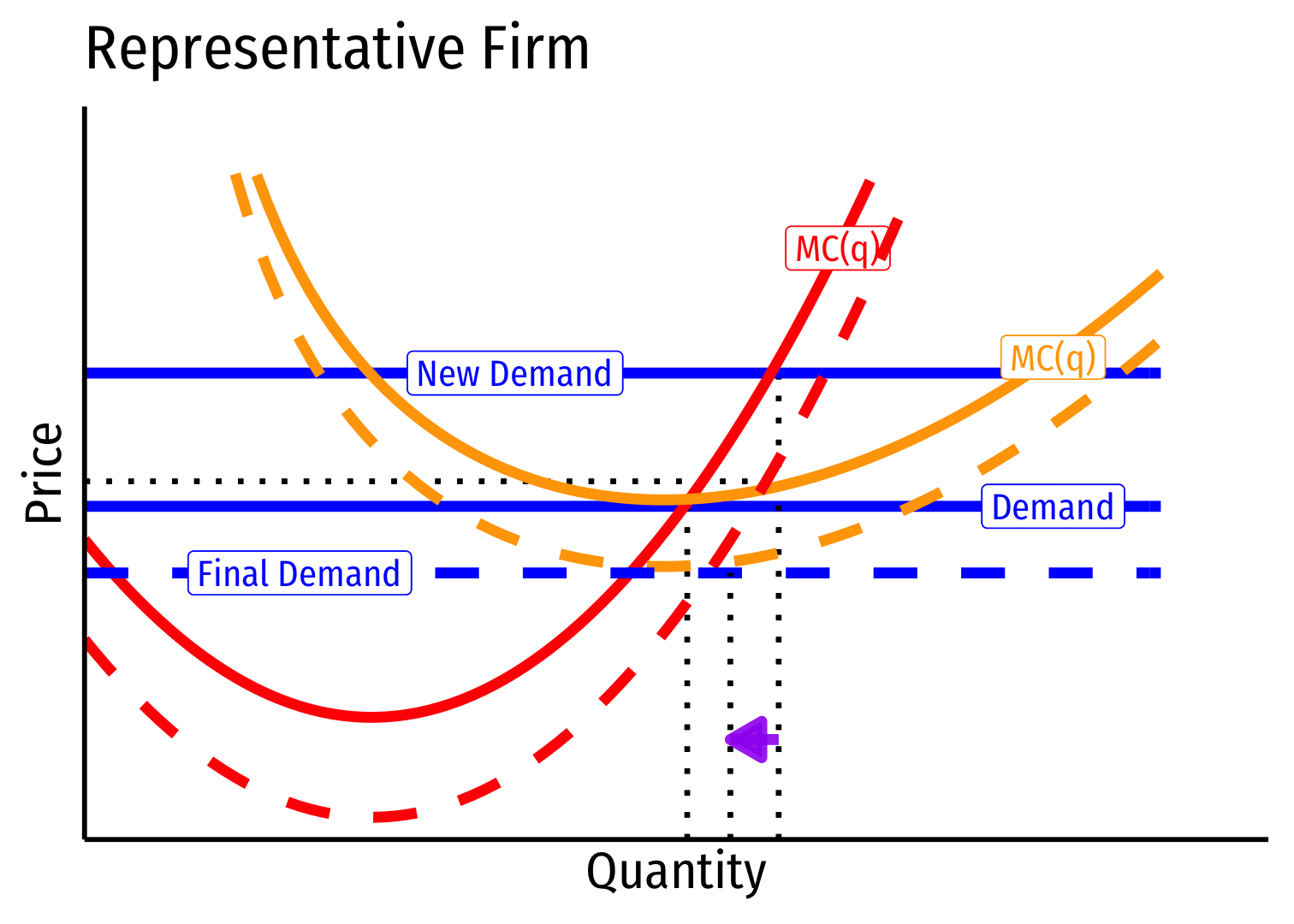
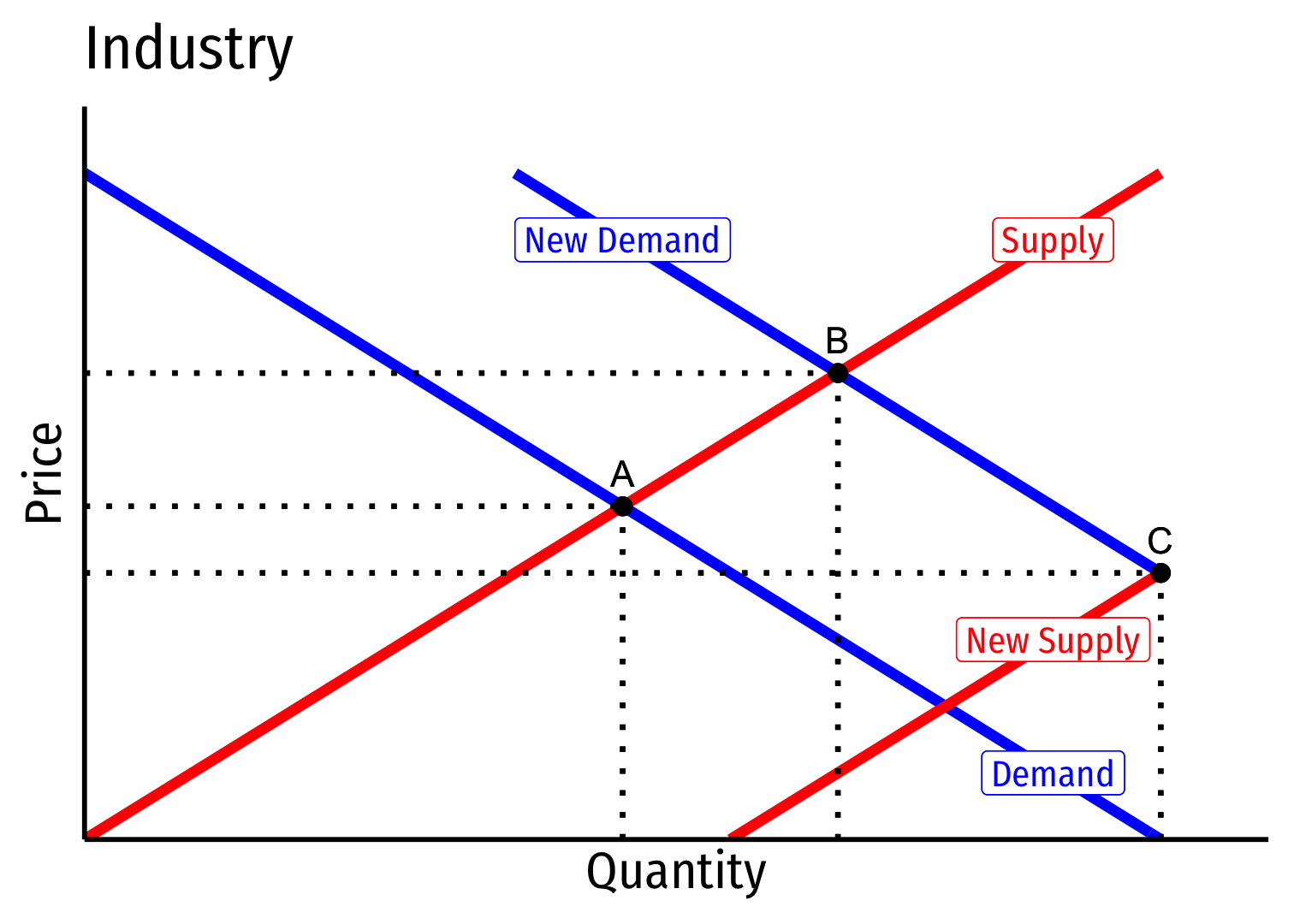
  • Long run (B→C): firms enter until π=0 at p=AC(q)

  • Firms charge higher p∗, producer lower q∗, earn π=0

Decreasing Cost Industry (External Economies) VII

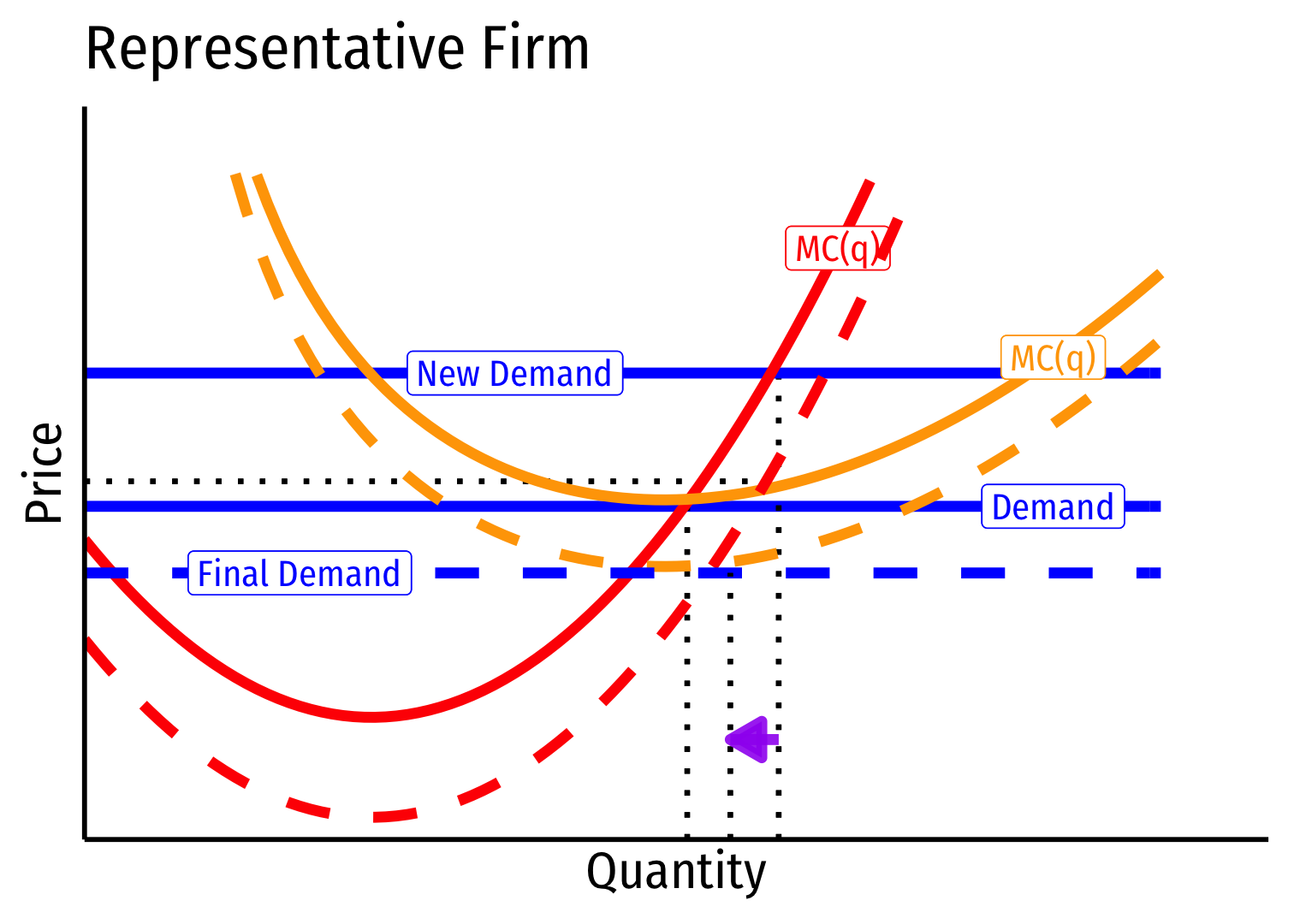
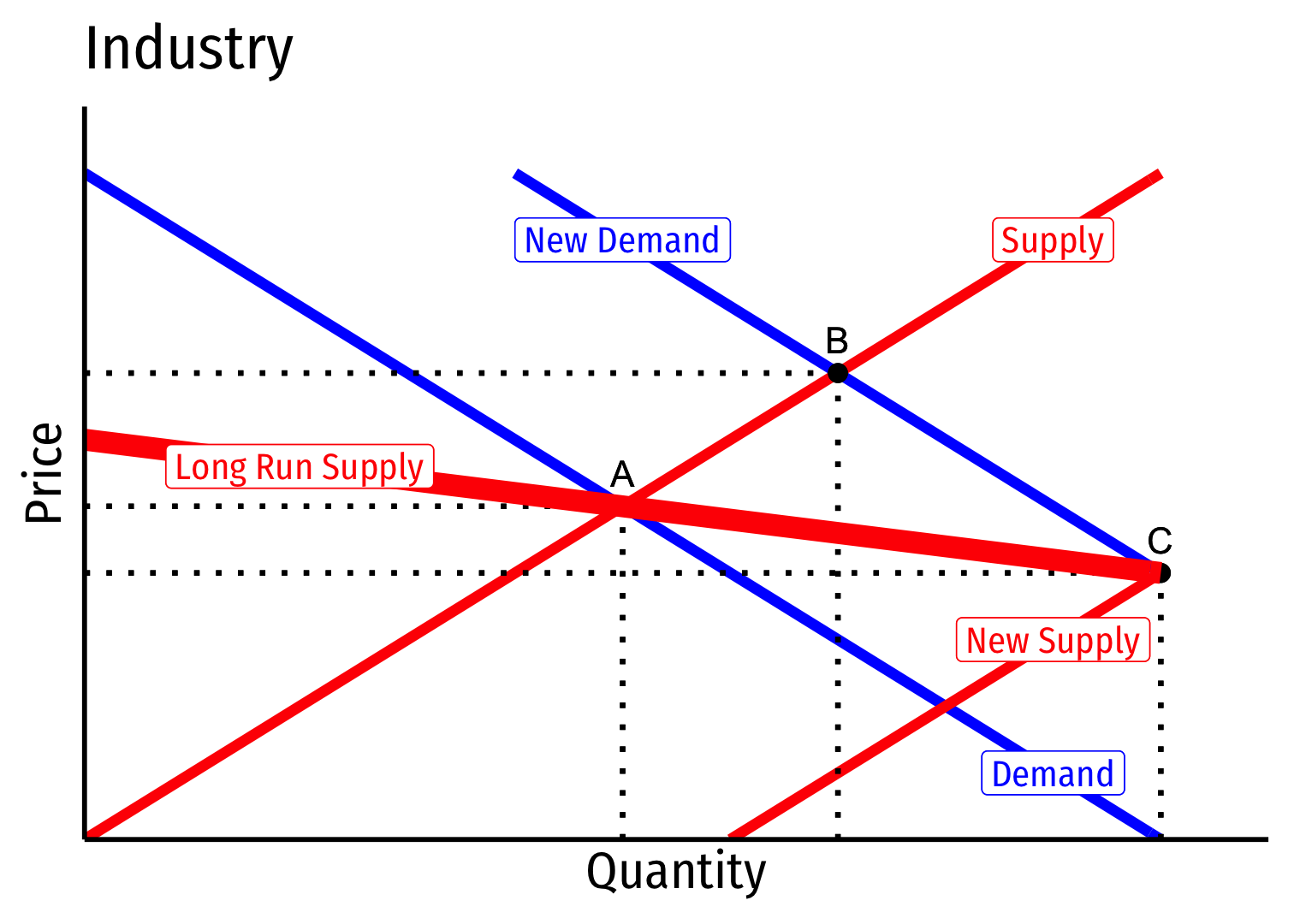
  • Long run industry supply curve is downward sloping!

Supply Functions

Supply Function

  • Supply function relates quantity supplied to price

Example: q=2p−4

  • Not graphable (wrong axes)!

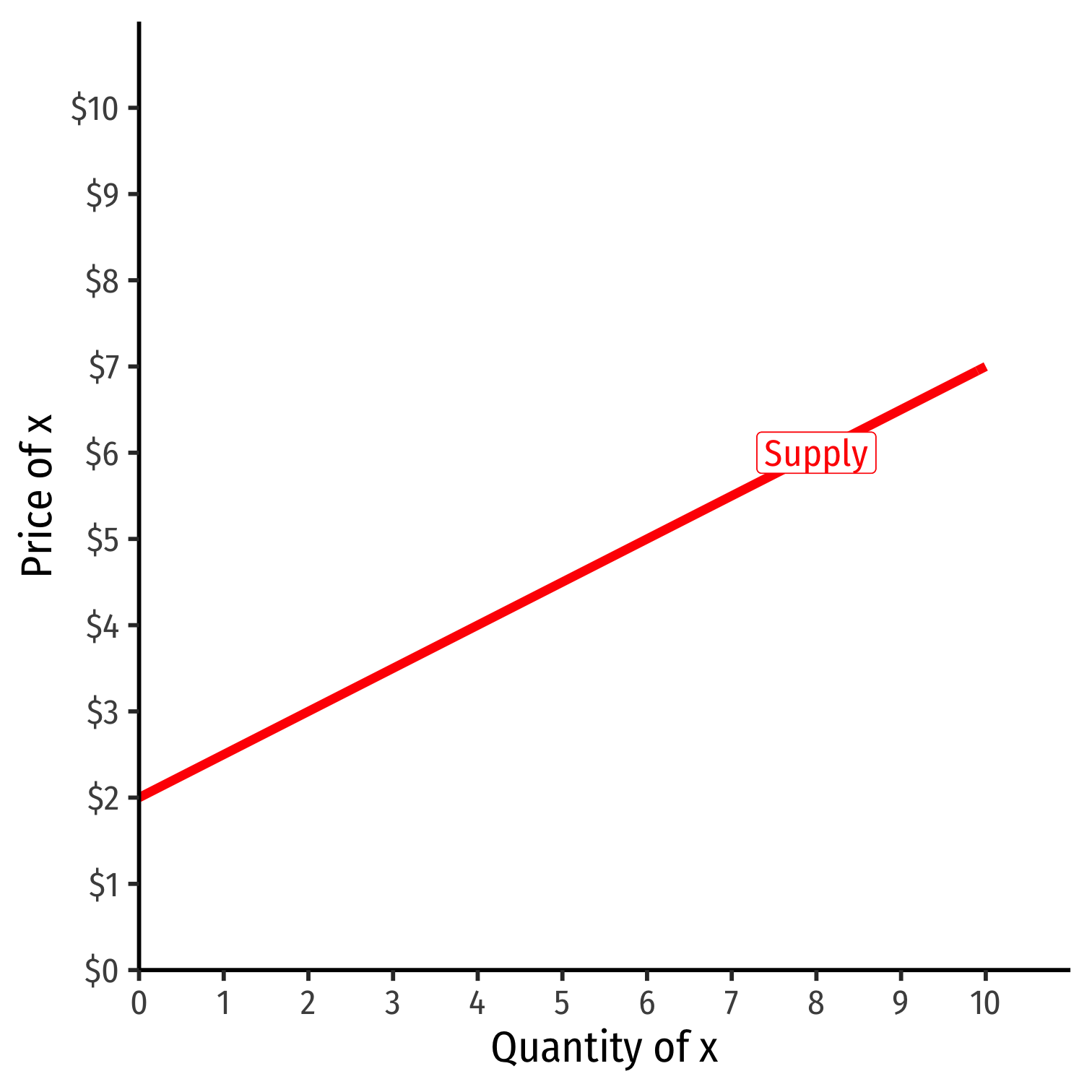
Inverse Supply Function

  • Inverse supply function relates price to quantity
    • Find by taking supply function and solving for p

Example: p=2+0.5q

  • Graphable (price on vertical axis)!

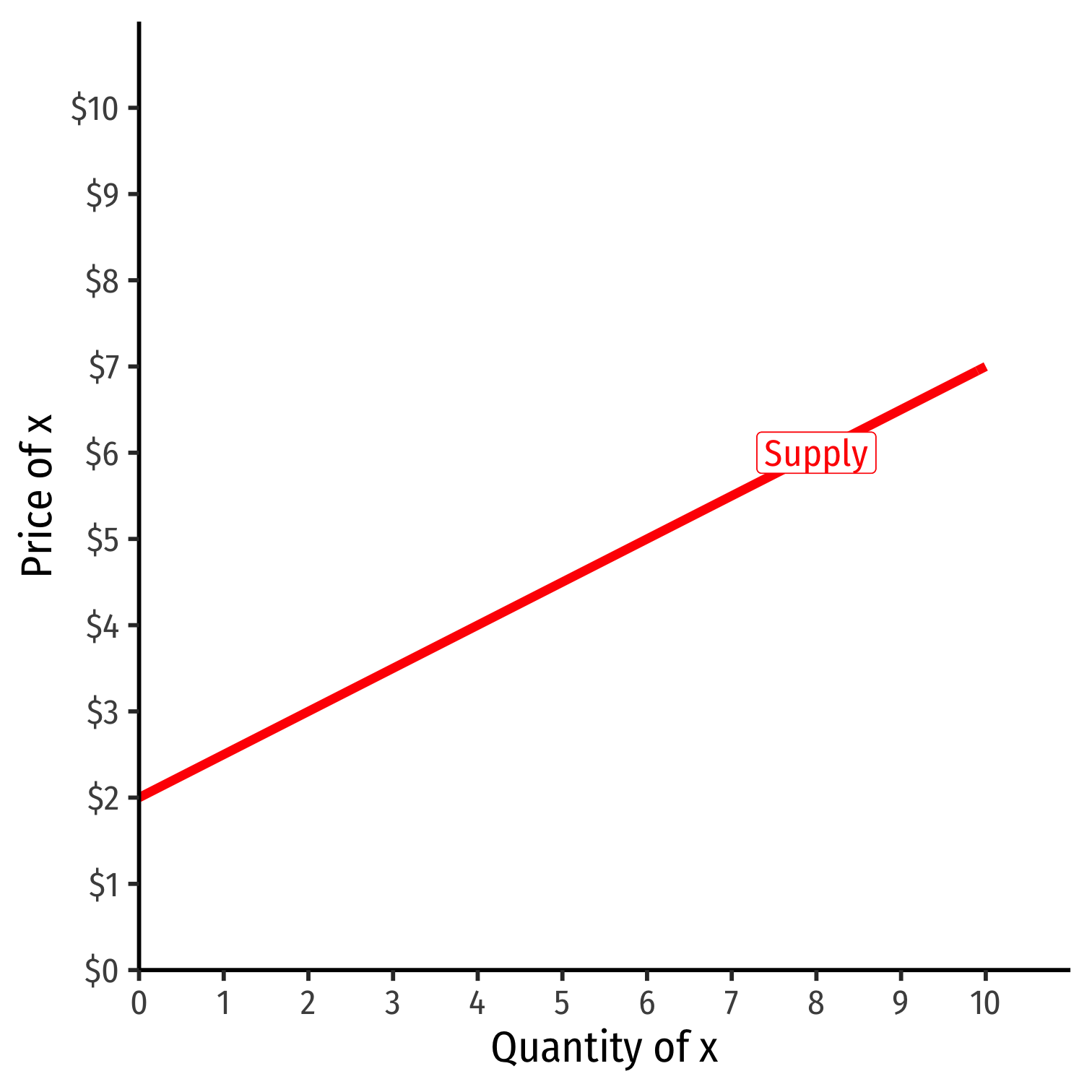
Inverse Supply Function

  • Supply demand function relates price to quantity
    • Find by taking demand function and solving for p

Example: p=2+0.5q

  • Graphable (price on vertical axis)!

  • Slope: 0.5

  • Vertical intercept called the "Choke price": price where qS=0 ($2), just low enough to discourage any sales

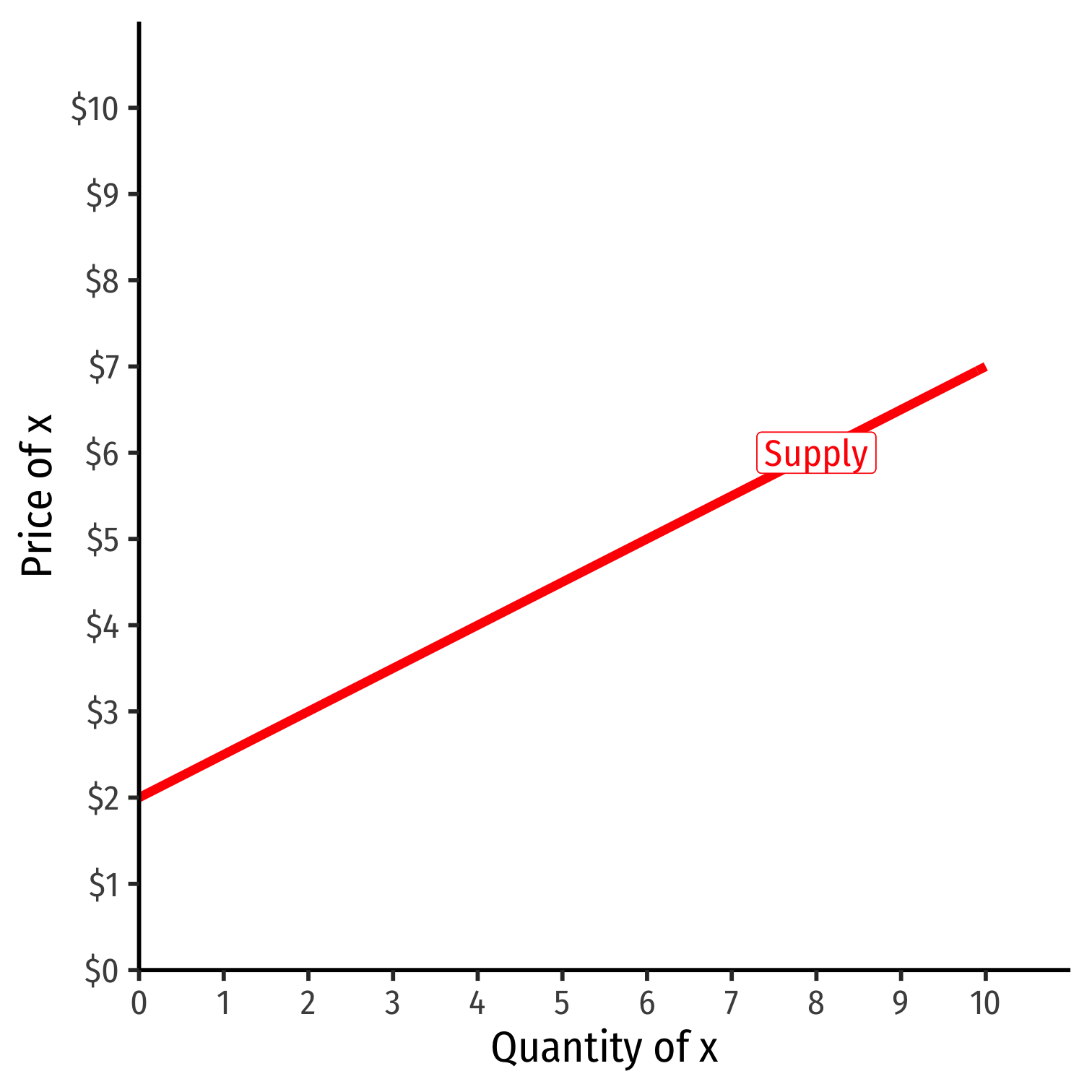
Inverse Supply Function

  • Inverse supply function relates price to quantity
    • Find by taking suuply function and solving for p

Example: p=2+0.5q

  • Read two ways:

  • Horizontally: at any given price, how many units firm wants to sell

  • Vertically: at any given quantity, the minimum willingness to accept (WTA) for that quantity

Price Elasiticity of Supply

Price Elasticity of Supply

  • Price elasticity of supply measures how much (in %) quantity supplied changes in response to a (1%) change in price

ϵqS,p=%ΔqS%Δp

Price Elasticity of Supply: Elastic vs. Inelastic

ϵqS,p=%ΔqS%Δp

"Elastic" "Unit Elastic" "Inelastic"
Intuitively: Large response Proportionate response Little response
Mathematically: ϵqs,p>1 ϵqs,p=1 ϵqs,p<1
Numerator > Denominator Numerator = Denominator Numerator < Denominator
A 1% change in p More than 1% change in qS 1% change in qS Less than 1% change in qS

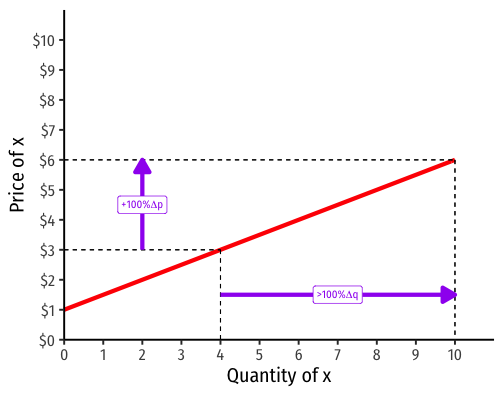
Visualizing Price Elasticity of Supply

An identical 100% price increase on an:

"Inelastic" Supply Curve

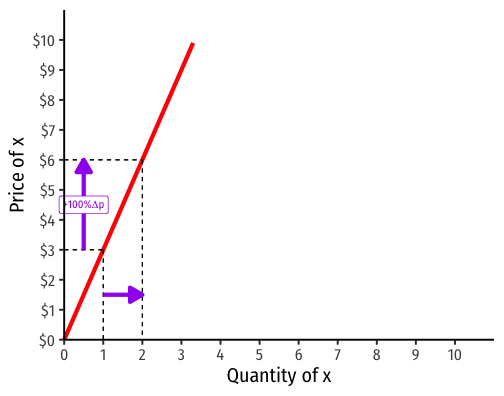
"Elastic" Supply Curve

Price Elasticity of Supply Formula

ϵq,p=1slope×pq

  • First term is the inverse of the slope of the inverse supply curve (that we graph)!

  • To find the elasticity at any point, we need 3 things:

    1. The price
    2. The associated quantity supplied
    3. The slope of the (inverse) supply curve

Example

Example: The supply of bicycle rentals in a small town is given by:

qS=10p−200

  1. Find the inverse supply function.

  2. What is the price elasticity of supply at a price of $25.00?

  3. What is the price elasticity of supply at a price of $50.00?

Price Elasticity of Supply Changes Along the Supply Curve

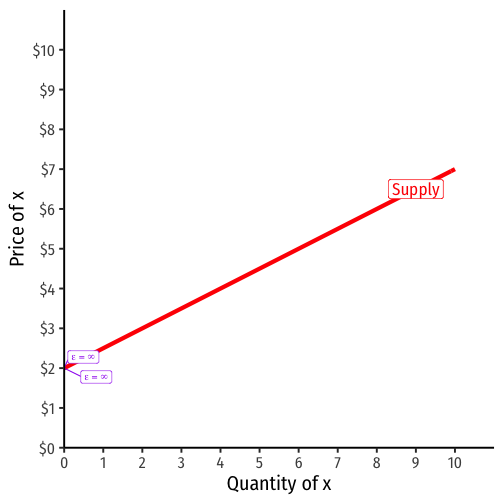
ϵq,p=1slope×pq

  • Elasticity ≠ slope (but they are related)!

  • Elasticity changes along the supply curve

  • Often gets less elastic as ↑ price (↑ quantity)

    • Harder to supply more

Determinants of Price Elasticity of Supply I

What determines how responsive your selling behavior is to a price change?

  • Increasing/Decreasing/Constant Cost industry ⟹ less/more/perfectly elastic supply

    • Mining for natural resources vs. automated manufacturing

  • Smaller (larger) share of market for inputs ⟹ more (less) elastic

    • Will your suppliers raise the price much if you buy more?
    • How much competition is there in your input markets?

Determinants of Price Elasticity of Supply II

What determines how responsive your selling behavior is to a price change?

  • More (less) time to adjust to price changes ⟹ more (less) elastic

Firm's Long Run Supply Decisions

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow