+ - 0:00:00
Notes for current slide
Notes for next slide

1.8: Income and Substitution Effects

ECON 306 · Microeconomic Analysis · Fall 2019

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microf19
microF19.classes.ryansafner.com

A Demand Function (Again)

  • A consumer's quantity demanded (of good x), qDx is a function of their demand for good x, which depends on current market prices and their income

qDx=D(m,px,py)

  • We now want to examine how quantity demanded for x changes as each of these parameters change:
  1. Income effects (ΔqDxΔm): how qDx changes with changes in income
  2. Cross-price effects (ΔqDxΔpy): how qDx changes with changes in prices of other goods (e.g. y)
  3. (Own) Price effects (ΔqDxΔpx): how qDx changes with changes in price (of x)

The (Own) Price Effect

The (Own) Price Effect

  • Price effect: change in optimal consumption of a good associated with a change in its price, holding income and other prices constant

ΔqDxΔpx<0

The law of demand: as the price of a good rises, people will tend to buy less of that good (and vice versa)

  • i.e. the price effect is negative!

Decomposing the Price Effect

  • The price effect (law of demand) is actually the net result of two effects

Decomposing the Price Effect

  • The price effect (law of demand) is actually the net result of two effects

  • (Real) income effect: change in consumption due to change in real purchasing power

Decomposing the Price Effect

  • The price effect (law of demand) is actually the net result of two effects

  • (Real) income effect: change in consumption due to change in real purchasing power

  • Substitution effect: change in consumption due to change in relative prices

Decomposing the Price Effect

  • The price effect (law of demand) is actually the net result of two effects

  • (Real) income effect: change in consumption due to change in real purchasing power

  • Substitution effect: change in consumption due to change in relative prices

Price Effect=Real income effect+Substitution Effect

(Real) Income Effect

(Real) Income Effect

  • Suppose there is only 1 good to consume, x. You have a $100 income, and the price of x is $10. You consume 10 units of x

  • Suppose the price of x falls to $5. Your now consume 20 units of x.

  • This is the real income effect: a change in the price of x changes your real income or purchasing power, the amount of goods you can buy

  • Note your actual (nominal) income of $100 never changed!

(Real) Income Effect: Size

  • The size of the income effect depends on how large a portion of your budget you spend on the good

  • Large-budget items:

    • e.g. Housing/apartment rent, car prices
    • Price increase makes you much poorer
    • Price decrease makes you much wealthier

  • Small-budget items:

    • e.g. pencils, toothpicks, candy
    • Price changes don't have much of an effect on your wealth or change your behavior much

Substitution Effect

Substitution Effect

  • Suppose there are 1000s of goods, none of them are a major fraction of your budget

  • Suppose the price of one good, x increases

  • The real income effect for x is tiny (and negative)

  • But you would consume less of x relative to other goods because x is now relatively more expensive

  • That's the substitution effect: consumption changes because of a change in relative prices

Substitution Effect: Size

  • The size of the substitution effect depends on how substitutable two goods are

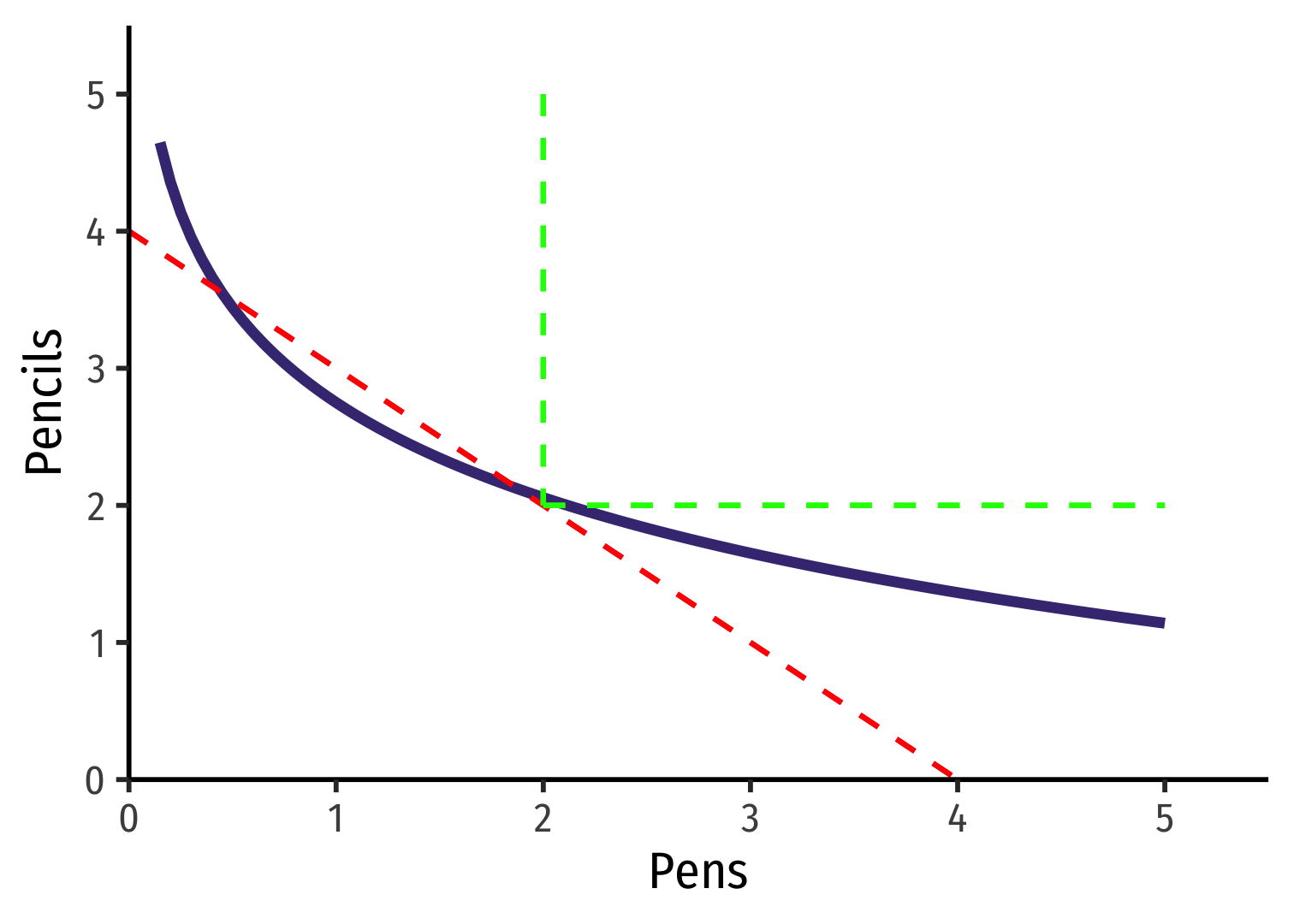
    • Straighter → more substitutable

Substitution Effect: Size

  • The size of the substitution effect depends on how substitutable two goods are

    • Straighter → more substitutable

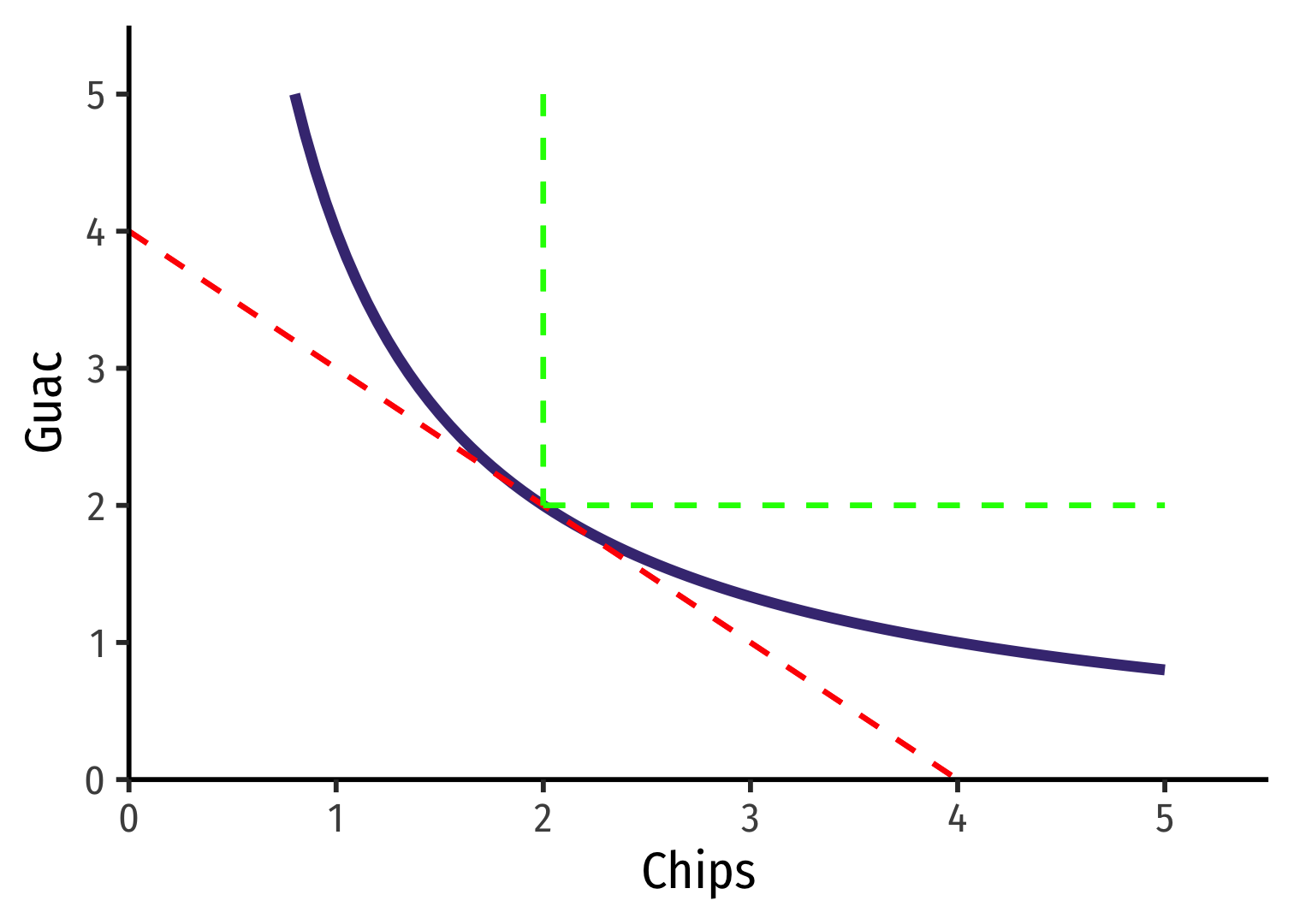
    • Curved → more complementary

Putting the Effects Together

Putting the Effects Together

  • Real income effect: change in consumption due to change in real purchasing power
    • Can be positive (normal goods) or negative (inferior goods)
    • Lower price of x means you can buy more x, y, or both (depending on your preferences between x and y)

Putting the Effects Together

  • Real income effect: change in consumption due to change in real purchasing power
    • Can be positive (normal goods) or negative (inferior goods)
    • Lower price of x means you can buy more x, y, or both (depending on your preferences between x and y)
  • Substitution effect: change in consumption due to change in relative prices
    • If x gets cheaper relative to y, consume ↓y (and ↑x)
    • This is always the same direction! (↓ relatively expensive goods, uparrow relatively cheaper goods)
    • This is why demand curves slope downwards!

Putting the Effects Together

  • Real income effect: change in consumption due to change in real purchasing power
    • Can be positive (normal goods) or negative (inferior goods)
    • Lower price of x means you can buy more x, y, or both (depending on your preferences between x and y)
  • Substitution effect: change in consumption due to change in relative prices
    • If x gets cheaper relative to y, consume ↓y (and ↑x)
    • This is always the same direction! (↓ relatively expensive goods, uparrow relatively cheaper goods)
    • This is why demand curves slope downwards!

Price Effect=Real income effect+Substitution Effect

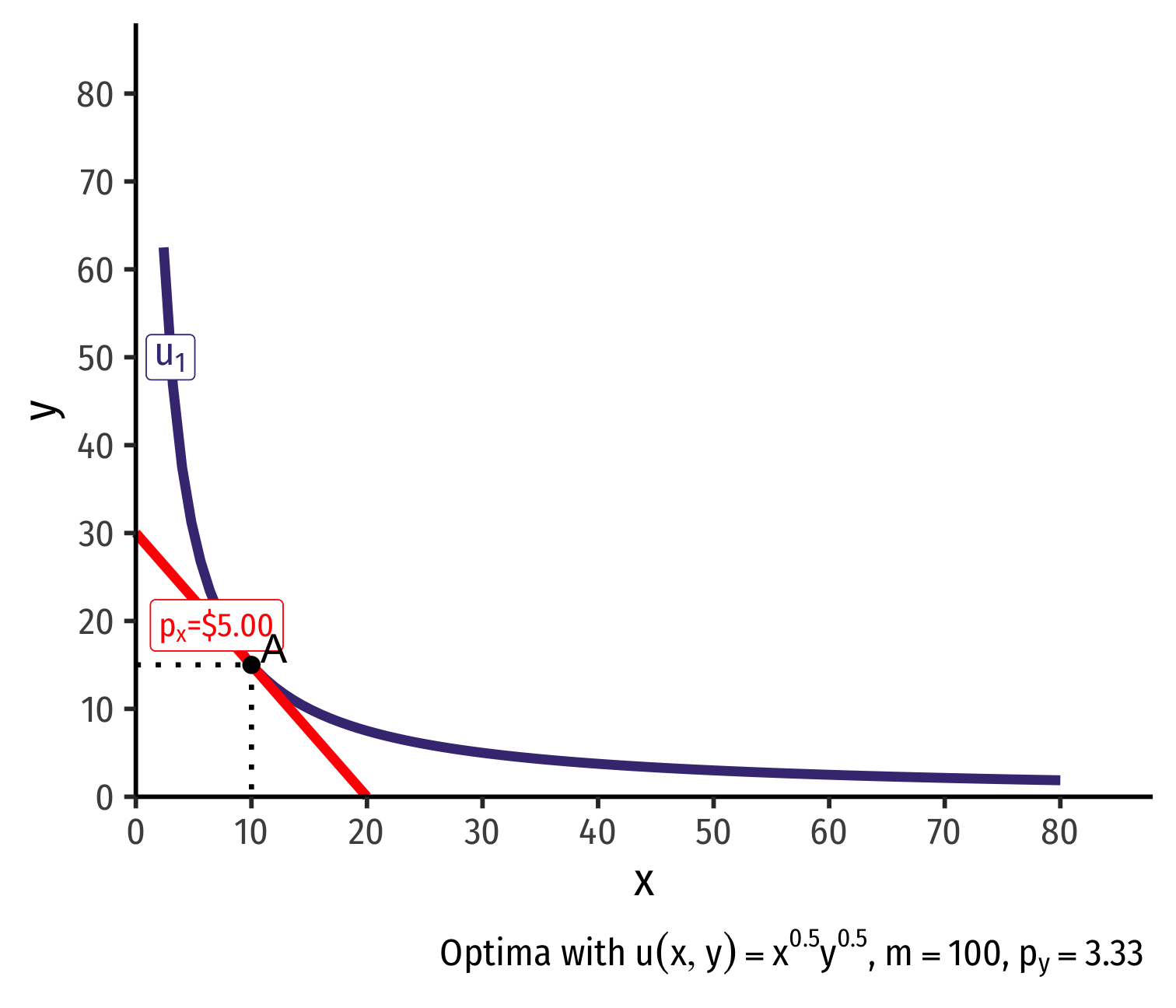
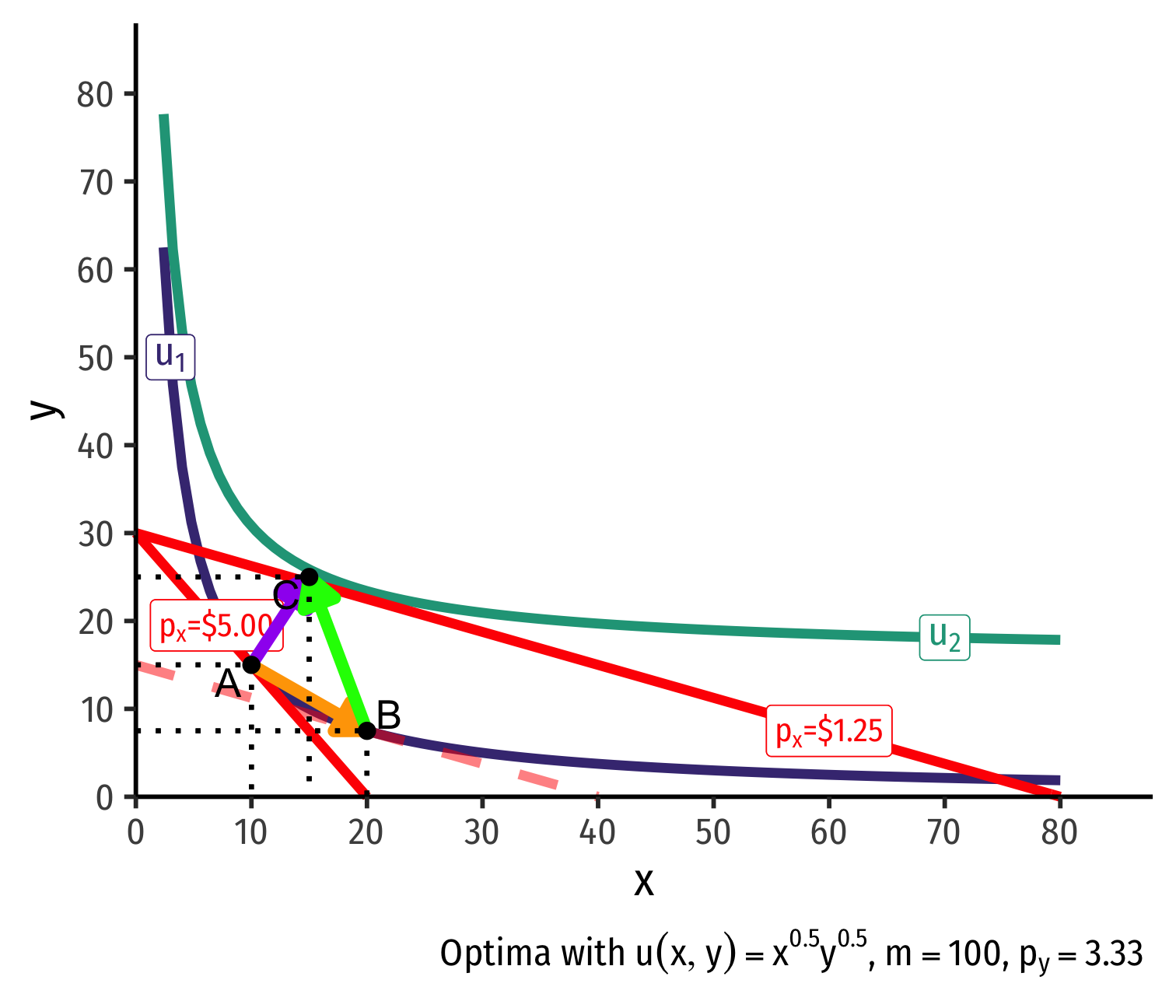
Real Income and Substitution Effects, Graphically I

  • Original optimal consumption (A)

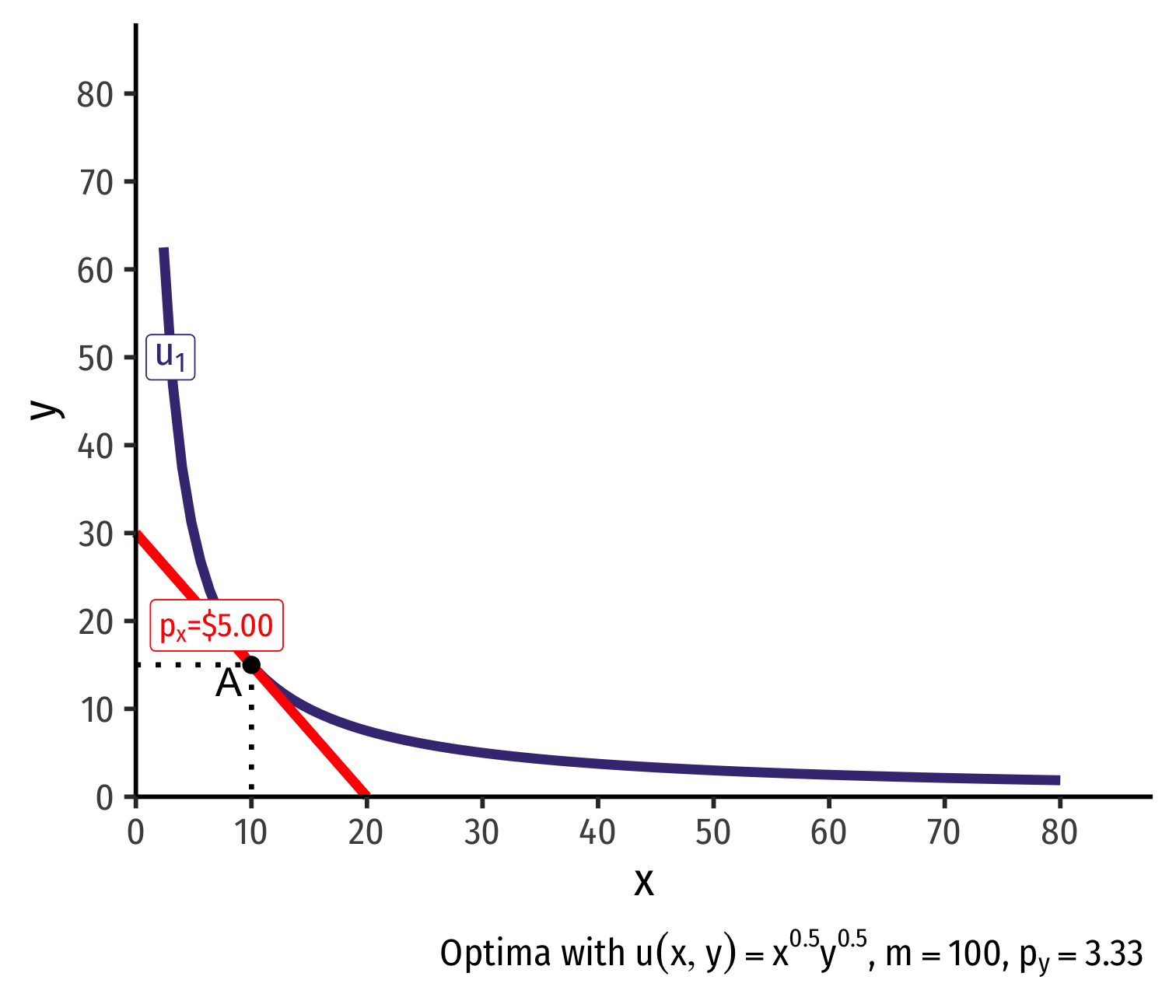
Real Income and Substitution Effects, Graphically I

  • Original optimal consumption (A)

  • (Total) price effect: A→C

  • Let's decompose this into the two effects

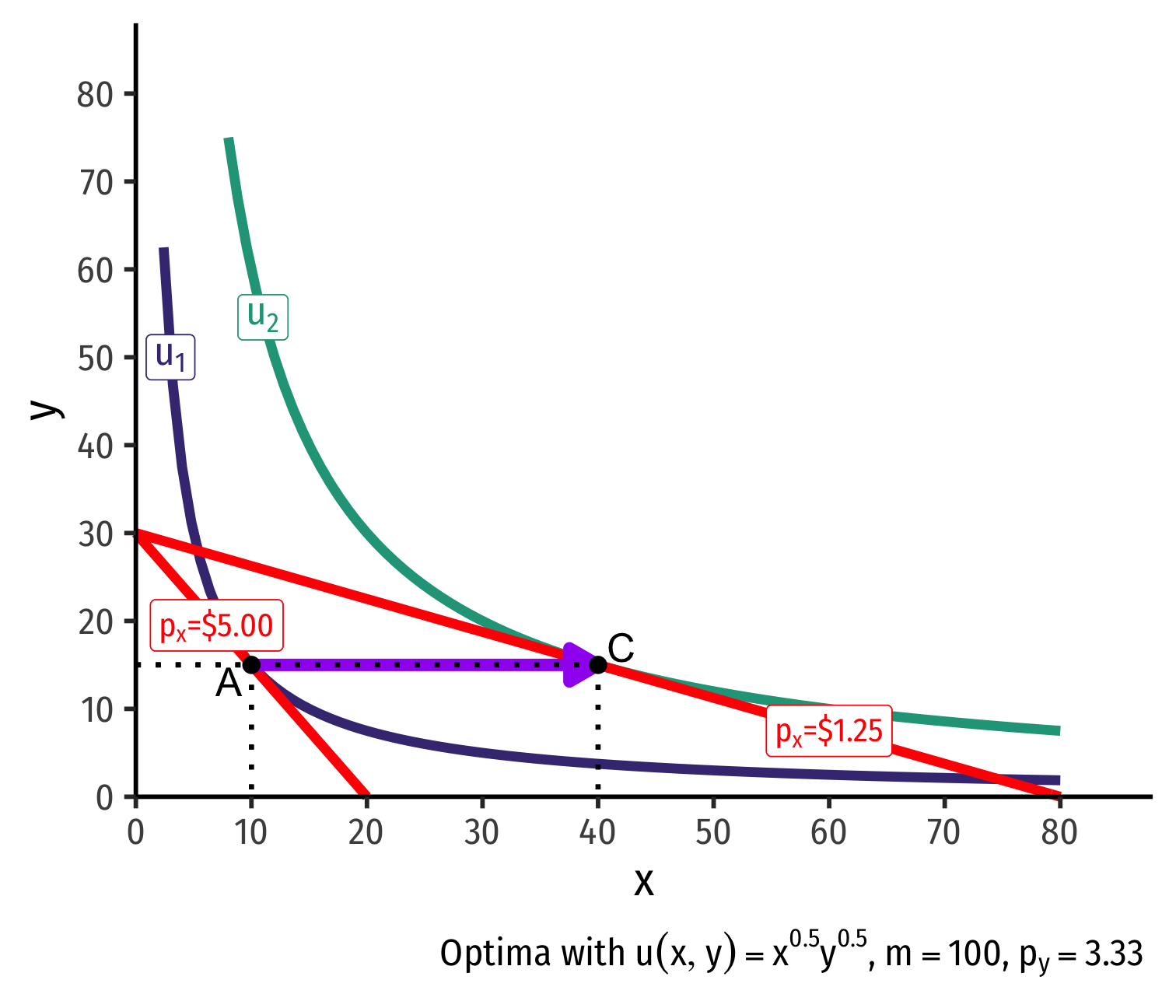
Real Income and Substitution Effects, Graphically II

  • Substitution effect: what would have been chosen at the new price ratio to remain indifferent as before

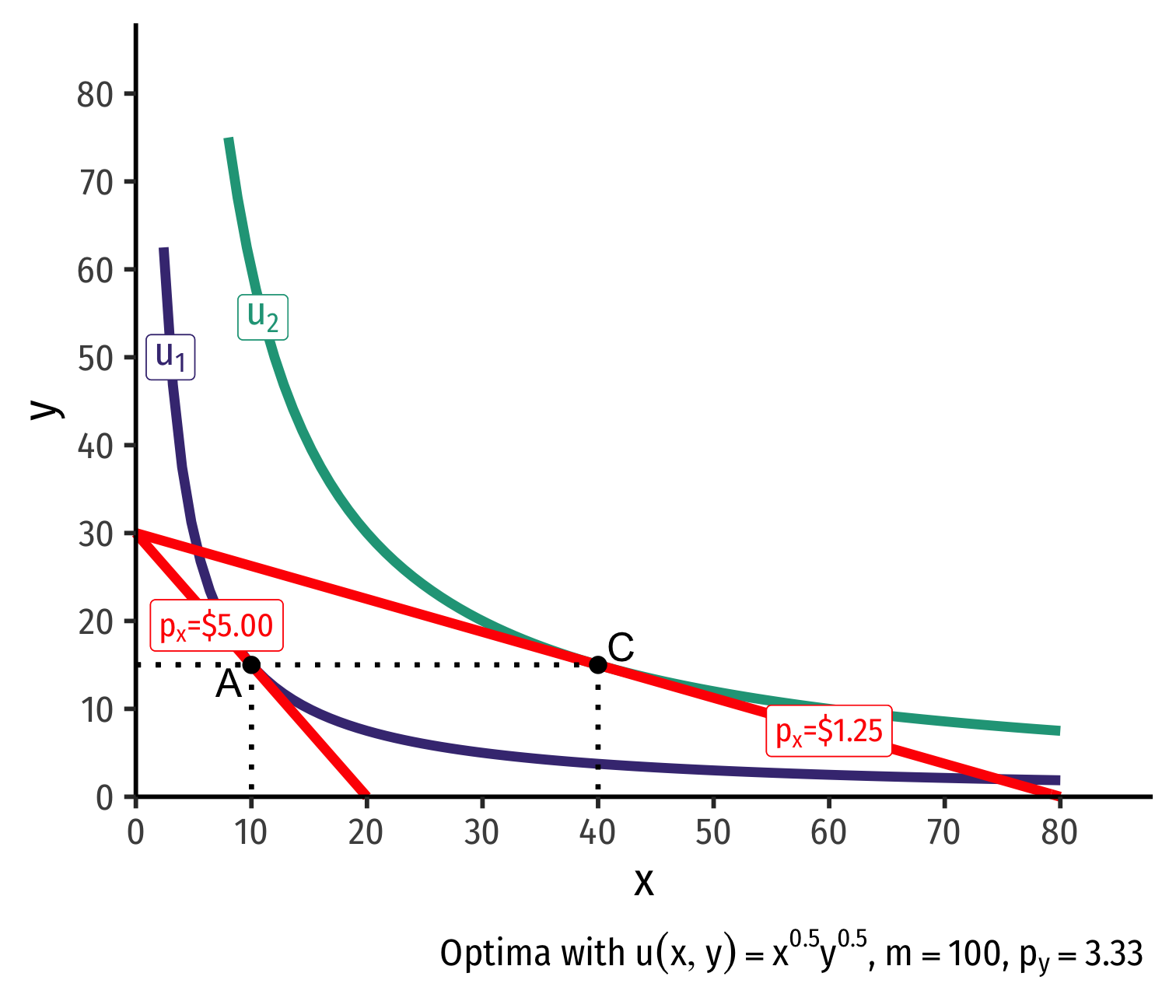
Real Income and Substitution Effects, Graphically II

  • Substitution effect: what would have been chosen at the new price ratio to remain indifferent as before

  • Graphically: shift new budget constraint inwards until tangent with old indifference curve

  • A→B on same I.C. (↑ cheaper x and ↓ y)

    • Note it must be a different point on the original curve!

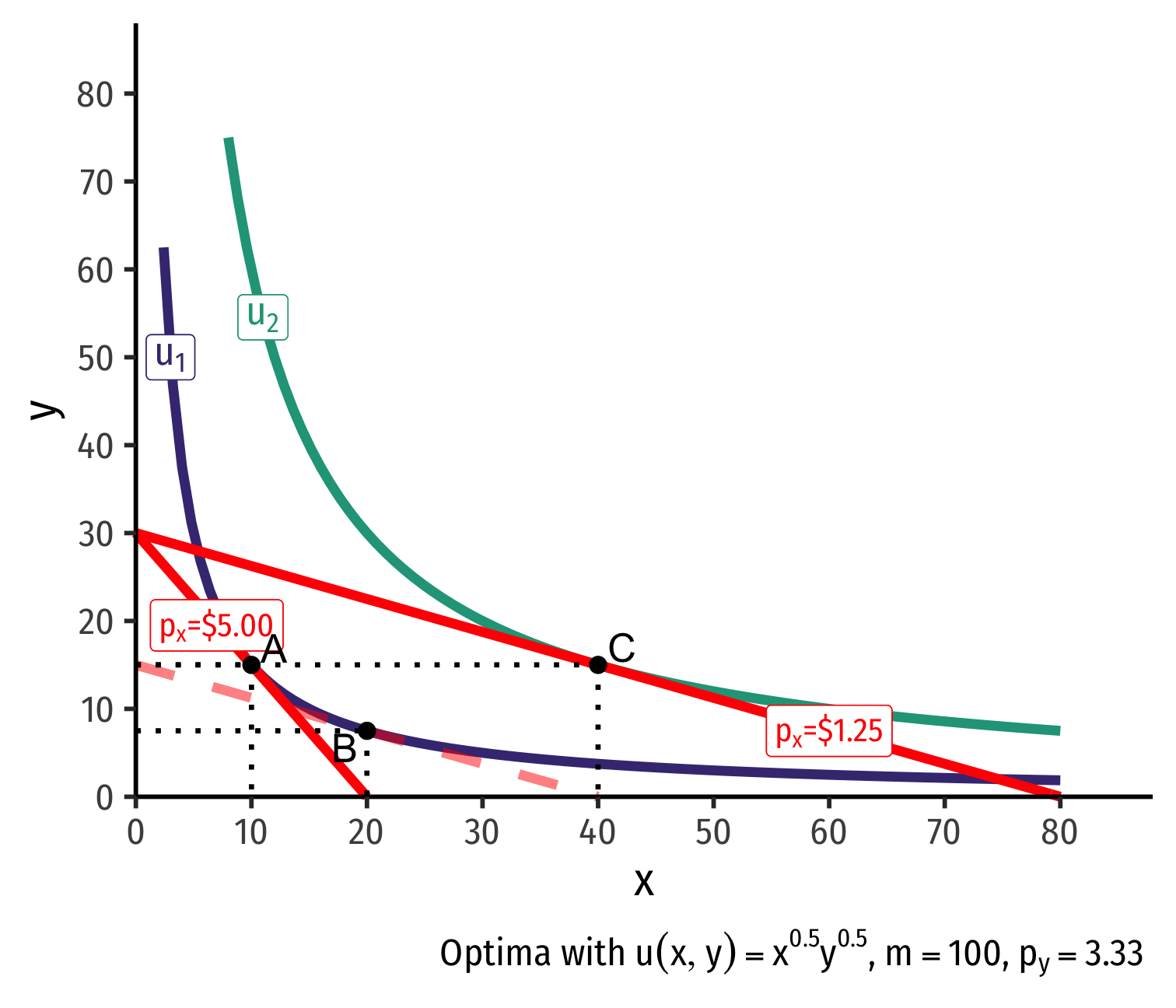
Real Income and Substitution Effects, Graphically II

  • Substitution effect: what would have been chosen at the new price ratio to remain indifferent as before

  • Graphically: shift new budget constraint inwards until tangent with old indifference curve

  • A→B on same I.C. (↑ cheaper x and ↓ y)

    • Note it must be a different point on the original curve!

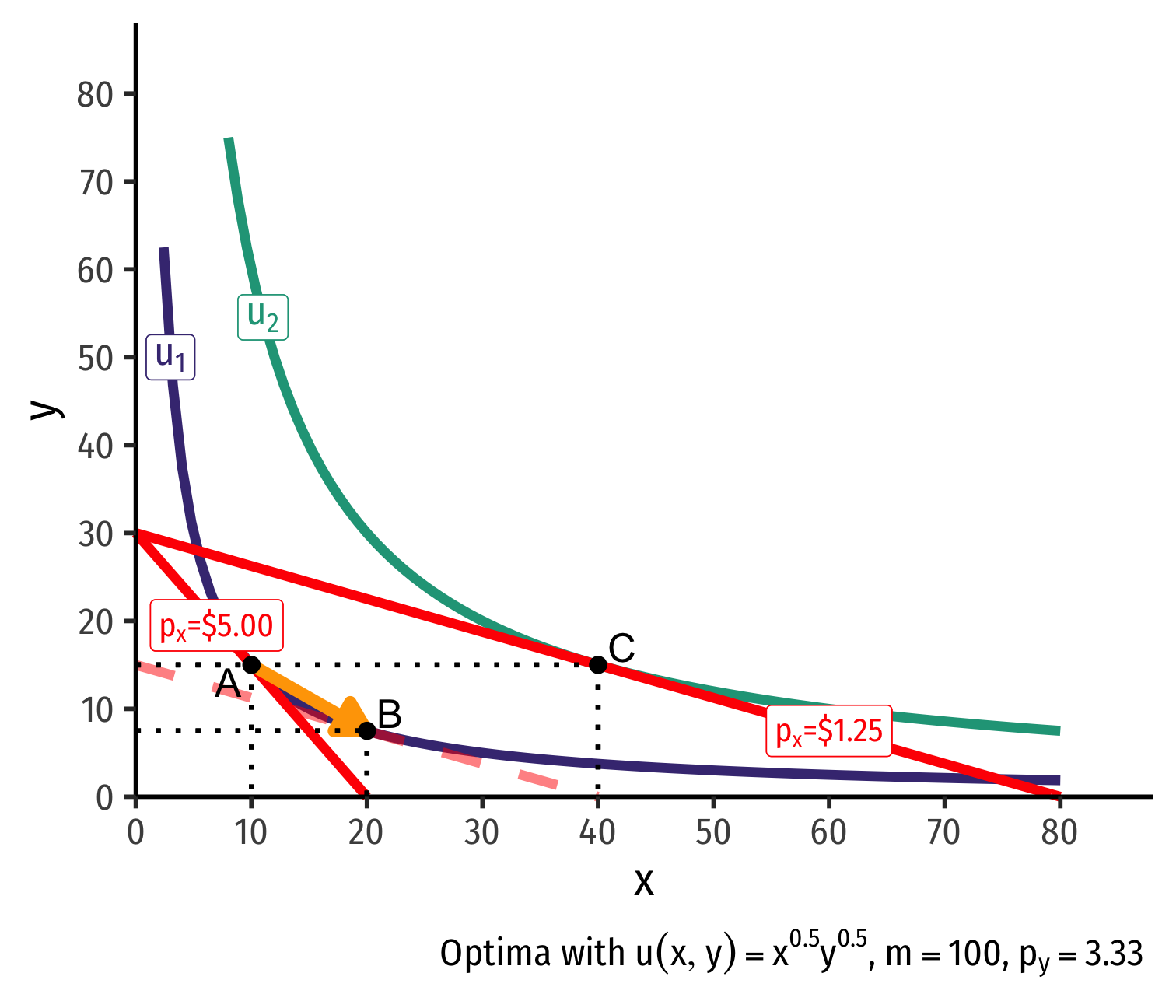
Real Income and Substitution Effects, Graphically III

  • (Real) income effect: change in quantities consumed due to the change in purchasing power after the change in price

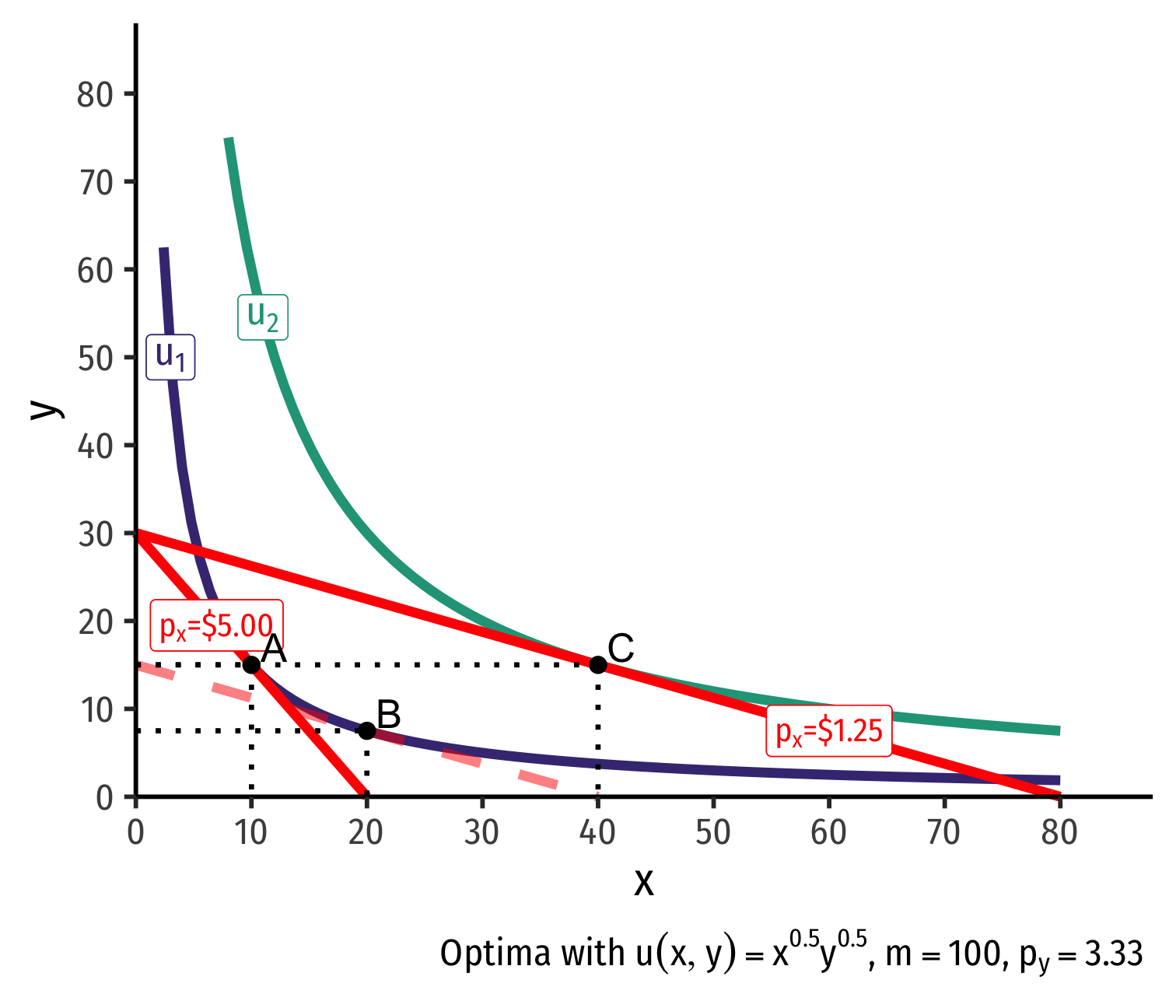
Real Income and Substitution Effects, Graphically III

  • (Real) income effect: change in quantities consumed due to the change in purchasing power after the change in price

  • B→C to new budget constraint (can buy more of x and/or y)

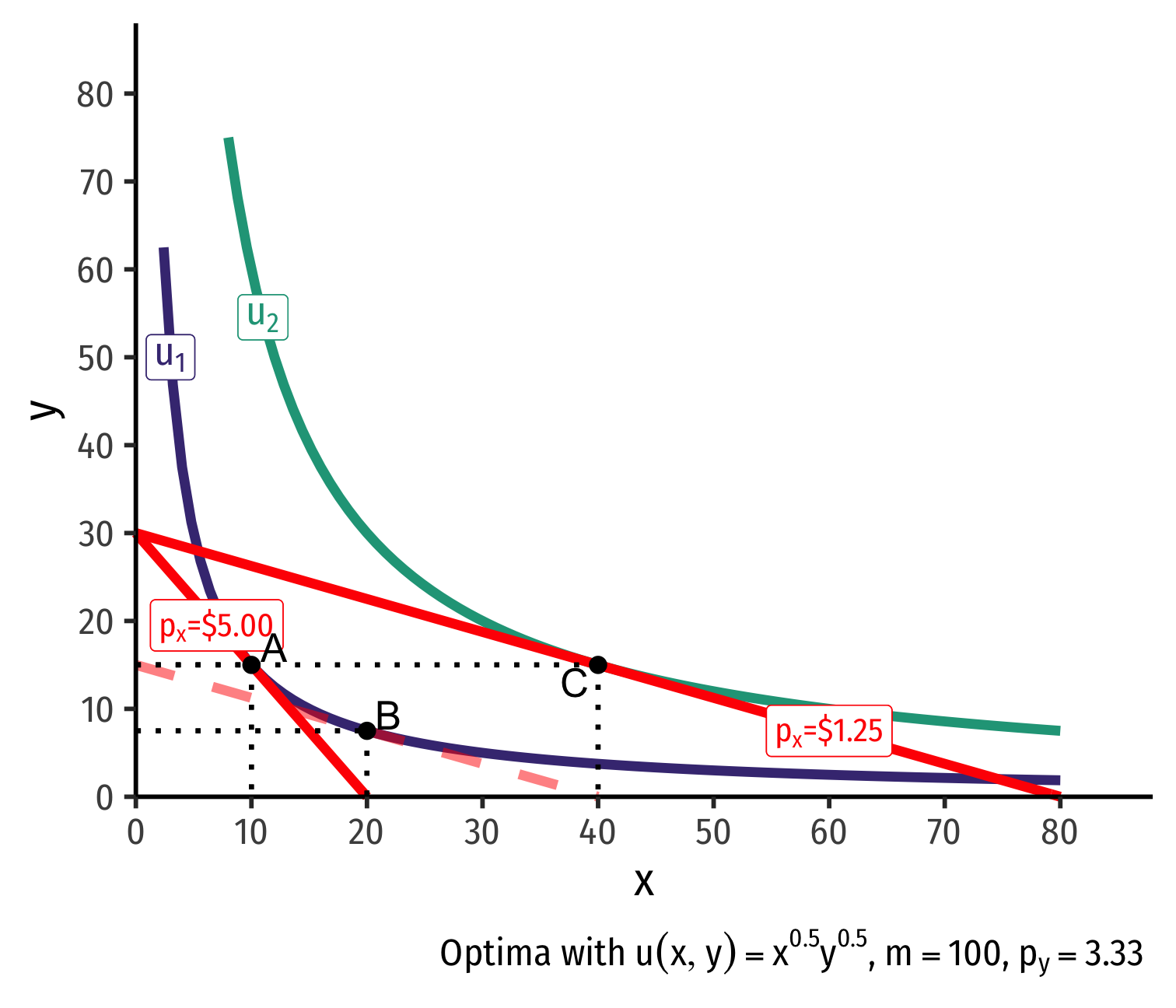
Real Income and Substitution Effects, Graphically III

  • (Real) income effect: change in quantities consumed due to the change in purchasing power after the change in price

  • B→C to new budget constraint (can buy more of x and/or y)

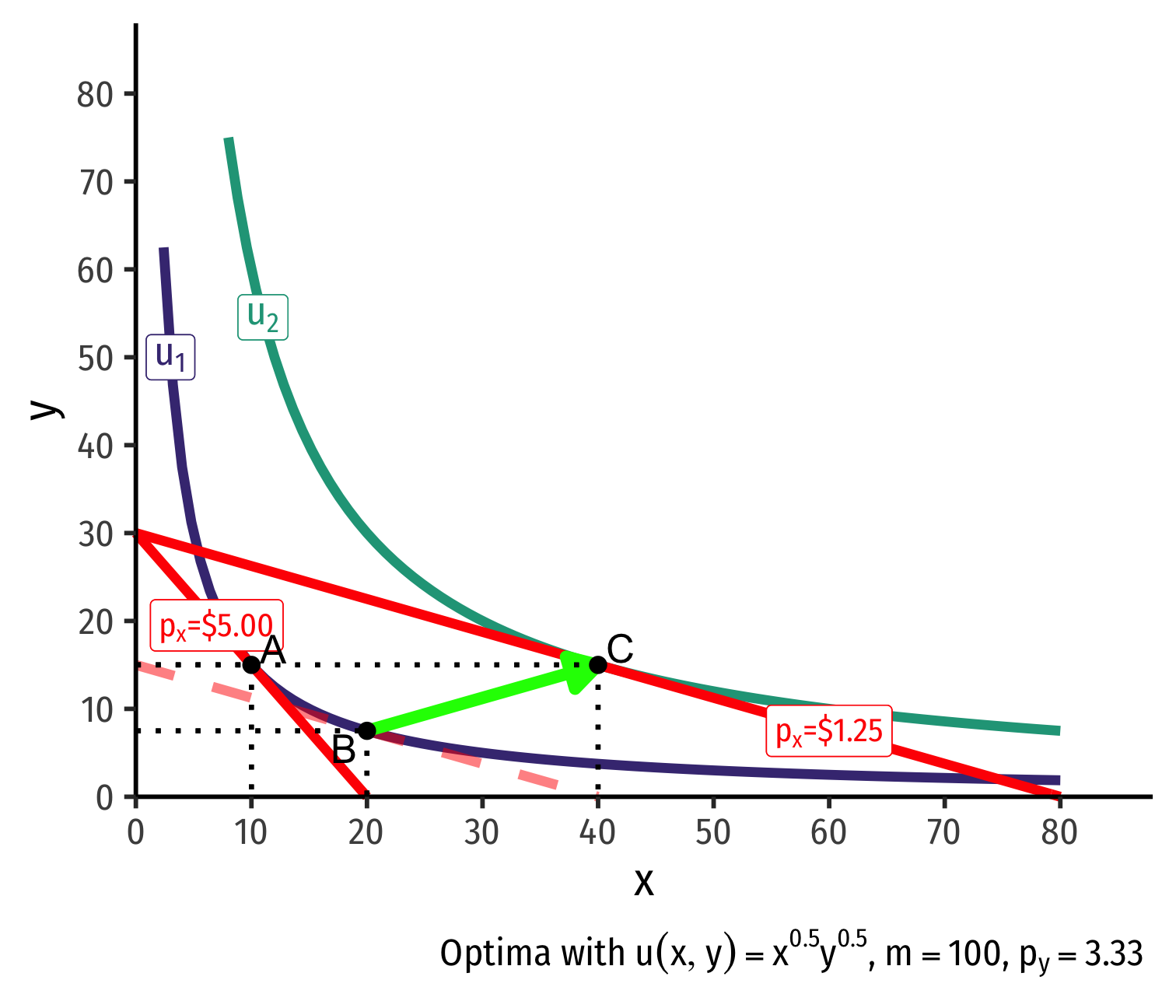
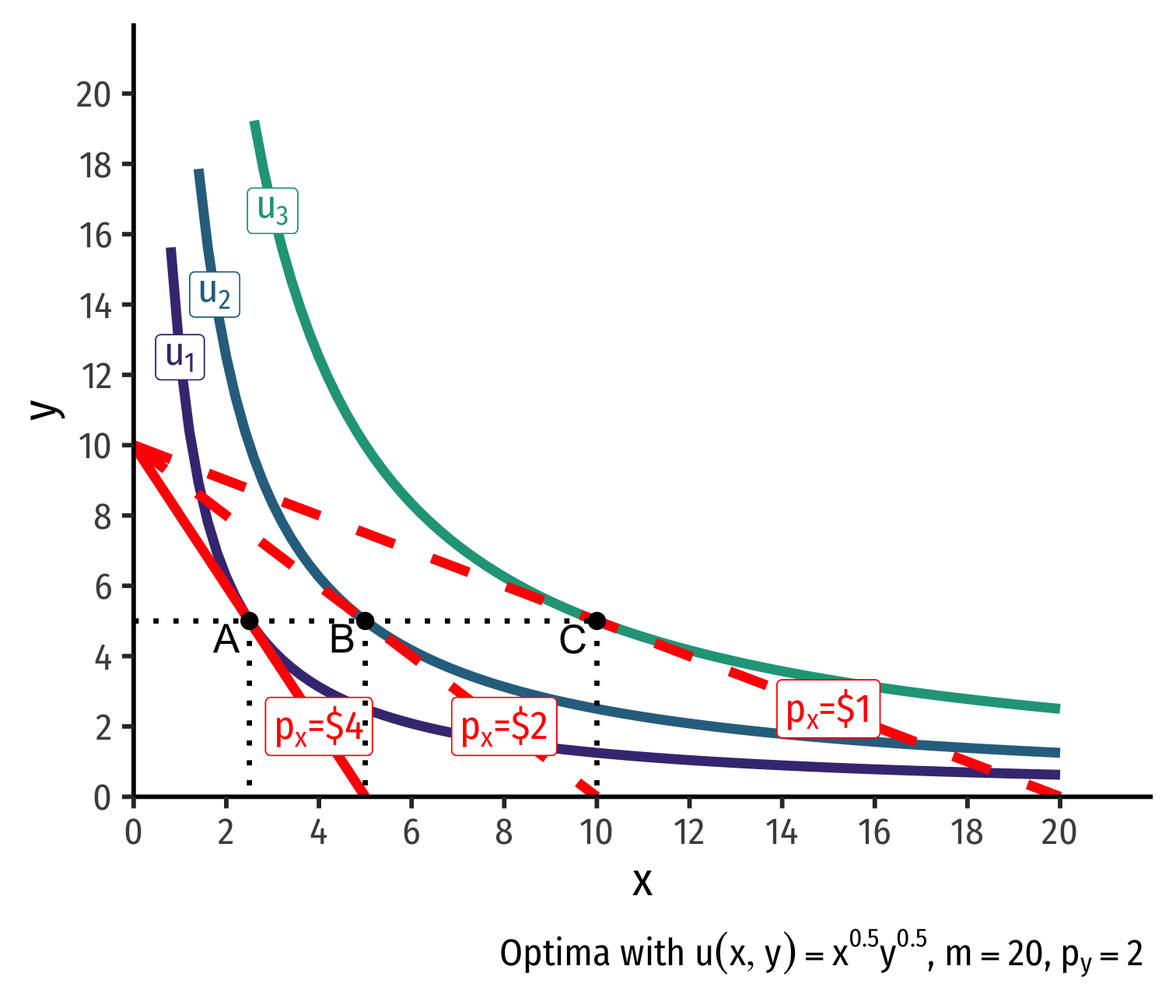
Real Income and Substitution Effects, Graphically IV

  • Original optimal consumption (A)

Real Income and Substitution Effects, Graphically IV

  • Original optimal consumption (A)

  • Price of x falls, new optimal consumption at (C)

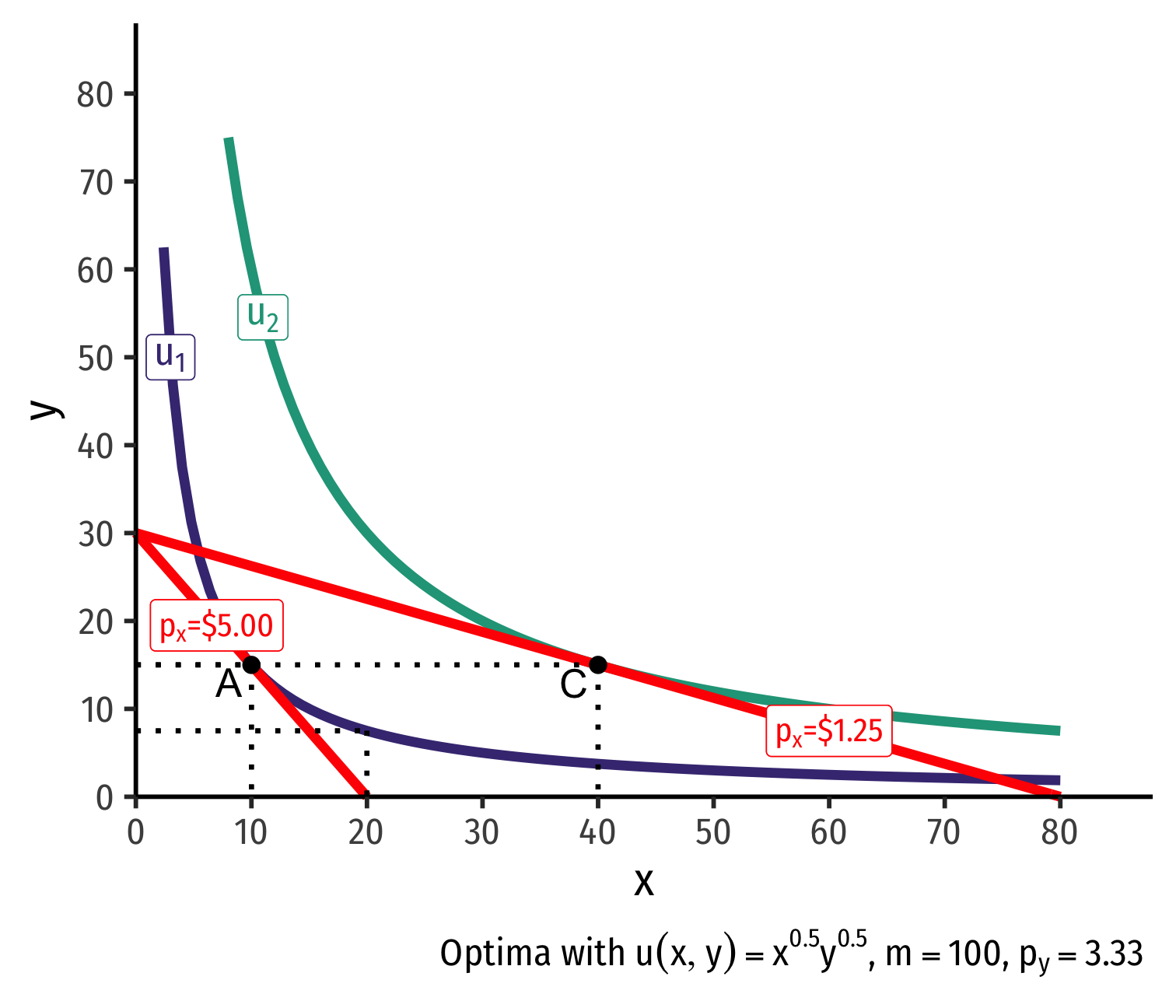
Real Income and Substitution Effects, Graphically IV

  • Original optimal consumption (A)

  • Price of x falls, new optimal consumption at (C)

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

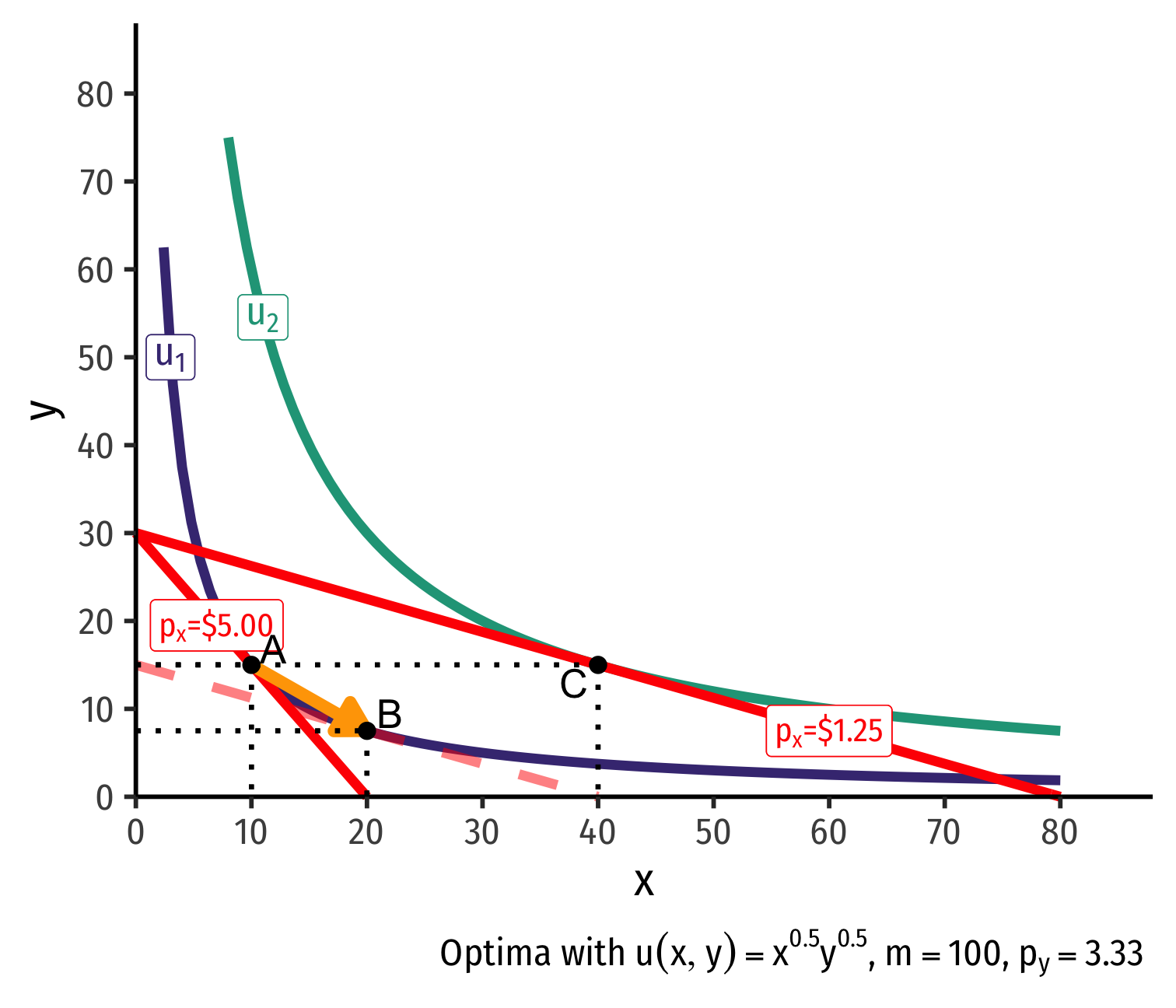
Real Income and Substitution Effects, Graphically IV

  • Original optimal consumption (A)

  • Price of x falls, new optimal consumption at (C)

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

  • (Real) income effect: B→C to new budget constraint (can buy more of x and/or y)

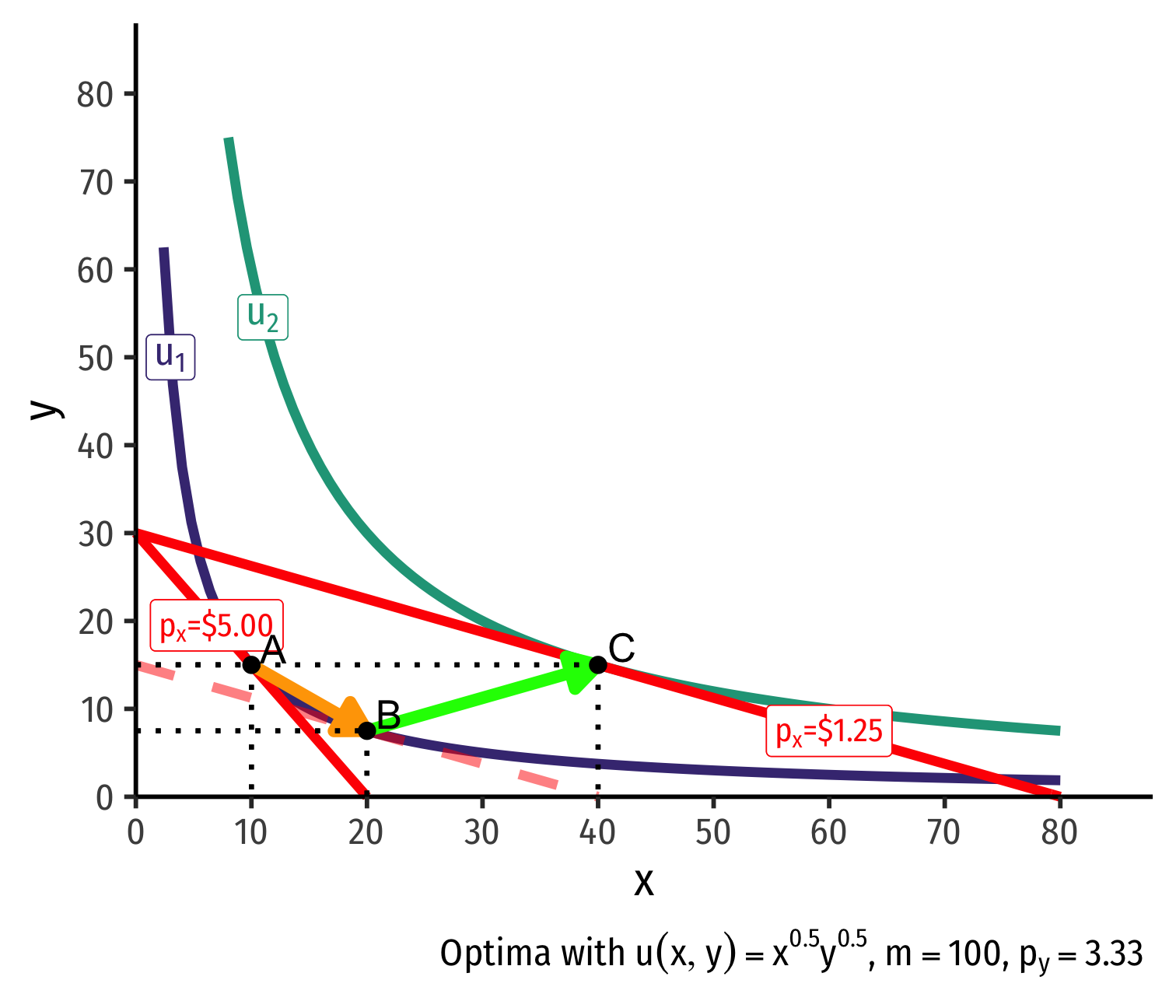
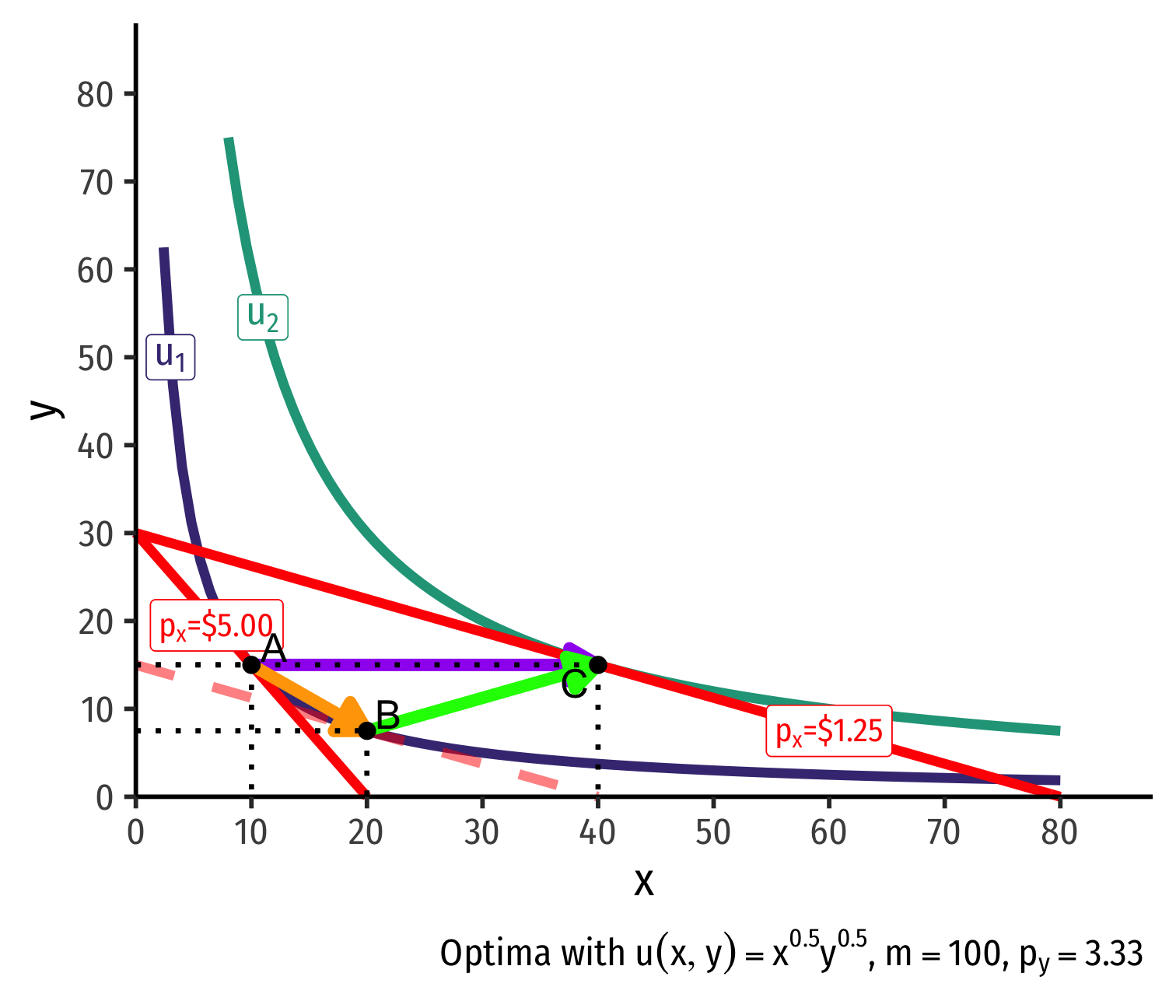
Real Income and Substitution Effects, Graphically IV

  • Original optimal consumption (A)

  • Price of x falls, new optimal consumption at (C)

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

  • (Real) income effect: B→C to new budget constraint (can buy more of x and/or y)

  • (Total) price effect: A→C

Real Income and Substitution Effects: Inferior Good

  • What about for an inferior good (like Ramen)?

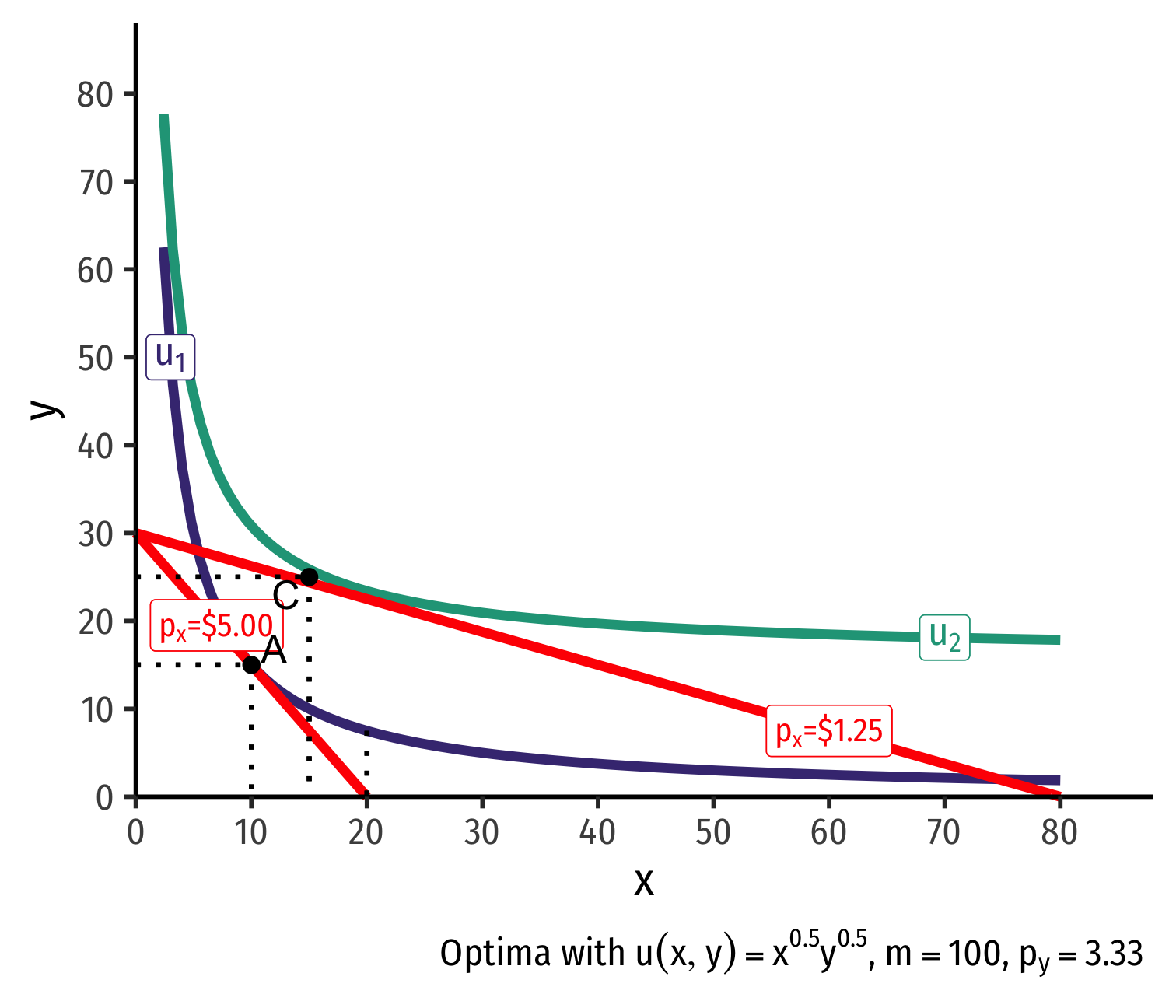
Real Income and Substitution Effects: Inferior Good

  • What about for an inferior good (like Ramen)?

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

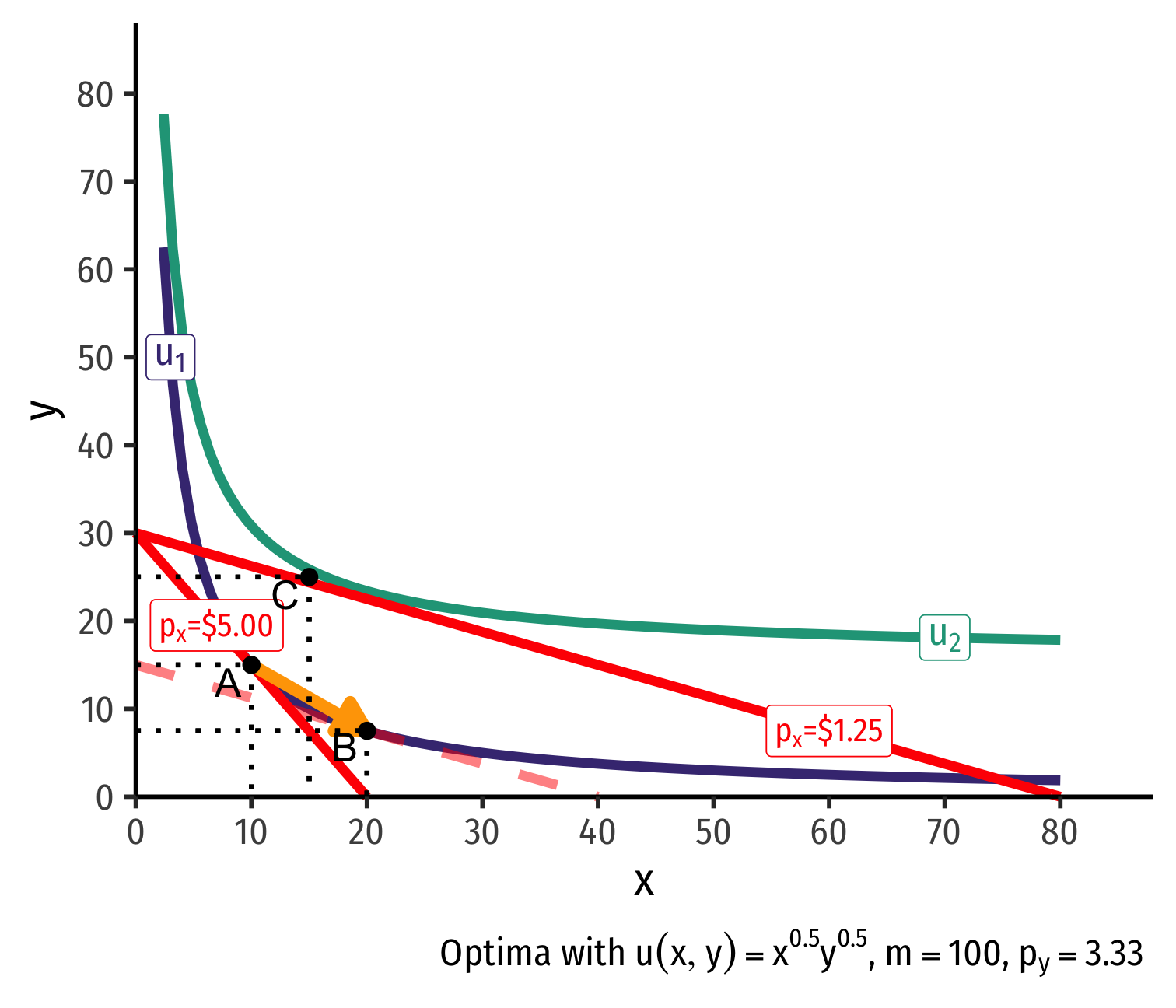
Real Income and Substitution Effects: Inferior Good

  • What about for an inferior good (like Ramen)?

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

  • (Real) income effect: B→C to new budget constraint (can buy more of x and/or y)

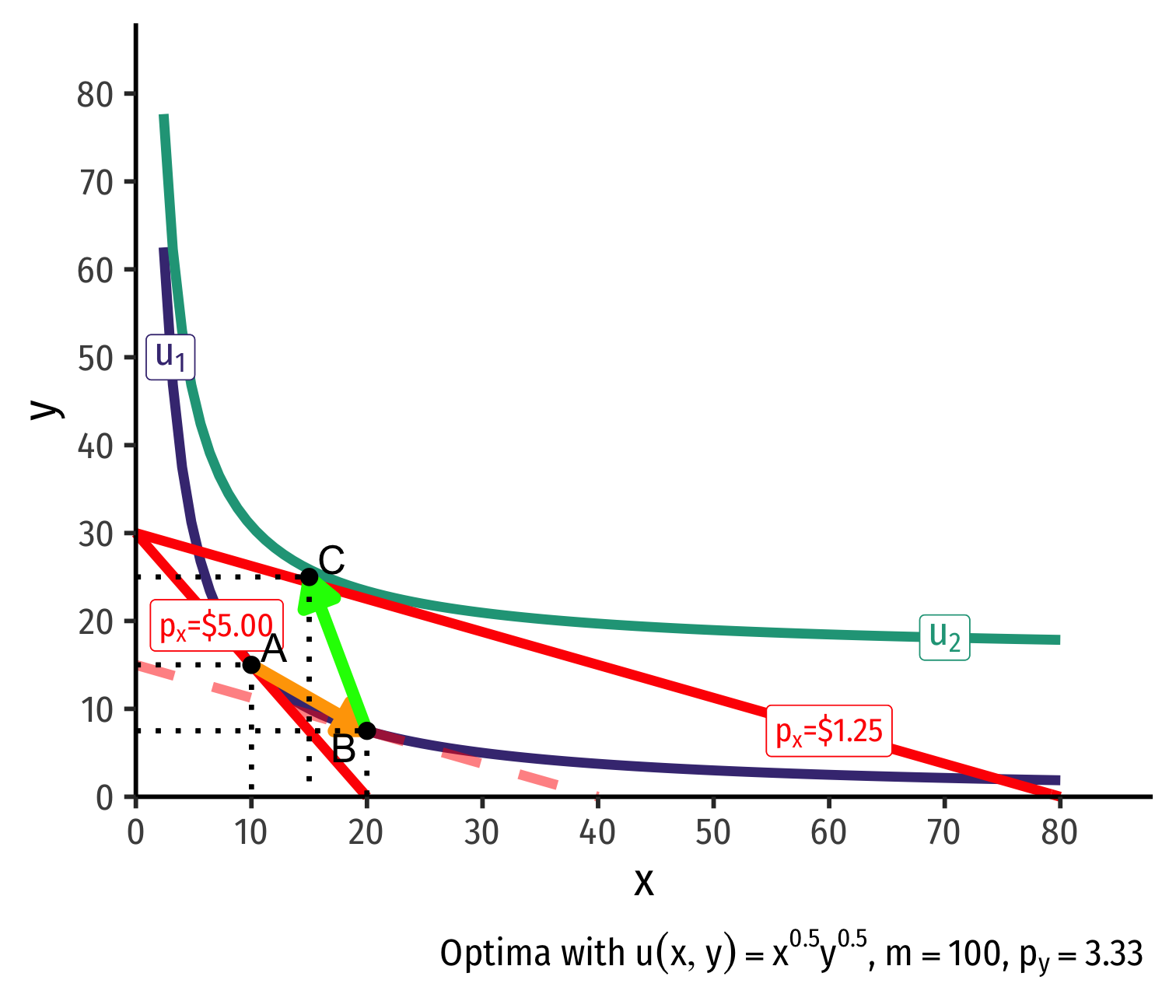
Real Income and Substitution Effects: Inferior Good

  • What about for an inferior good (like Ramen)?

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

  • (Real) income effect: B→C to new budget constraint (can buy more of x and/or y)

  • (Total) price effect: A→C

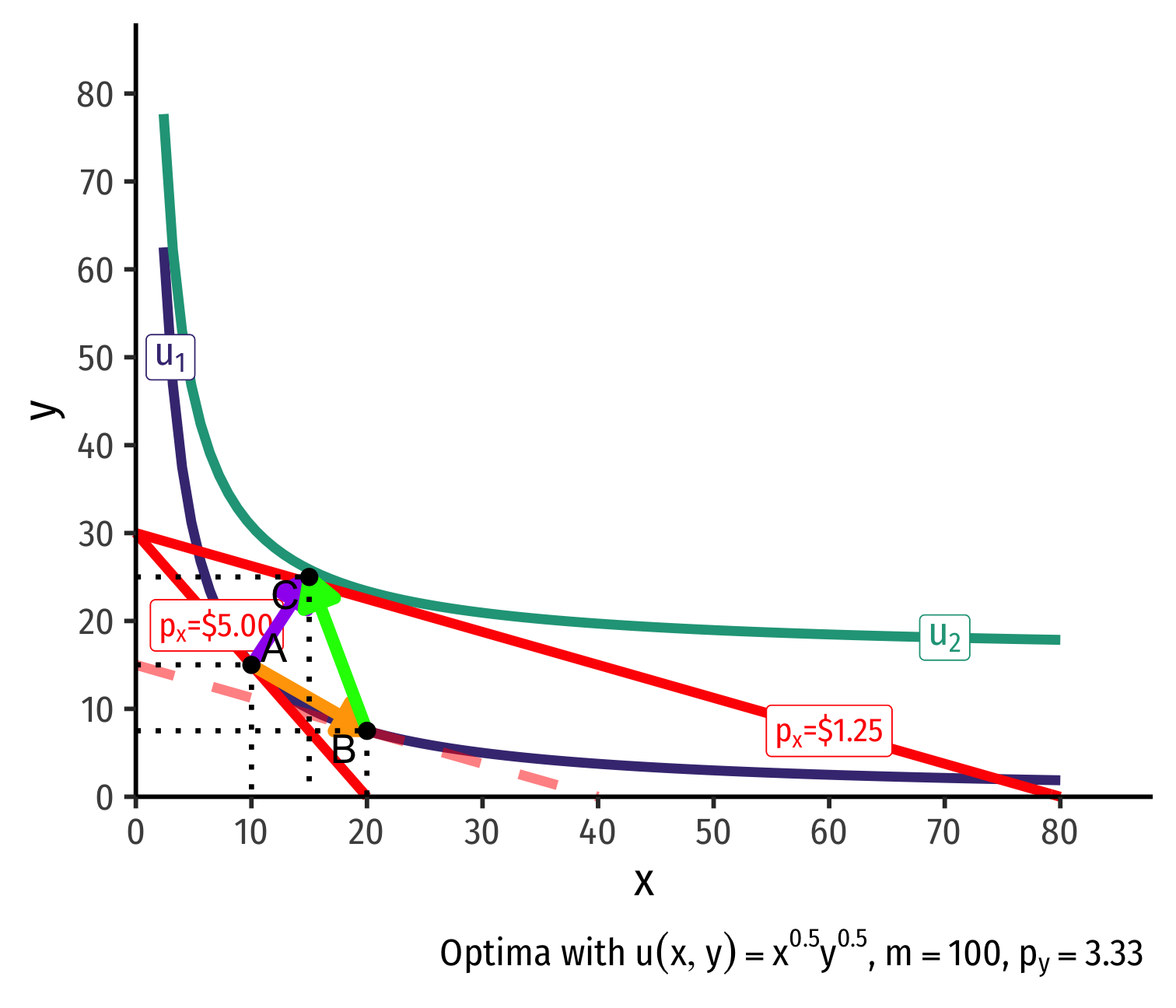
Real Income and Substitution Effects: Inferior Good

  • What about for an inferior good (like Ramen)?

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

  • (Real) income effect: B→C to new budget constraint (can buy more of x and/or y)

  • (Total) price effect: A→C

  • Price effect is still an ↑x from a ↓px!

    • Person would just prefer to spend more new purchasing power on other goods (y)!

  • The law of demand holds, even for inferior goods!

    • Because subst. effect dominates real income effect

Violating the Law of Demand

Example: What would it take to violate the law of demand?

Recap: Real Income and Substitution Effects

Substitution Effect+Real Income Effect=Price Effect

  • Substitution effect: is always in the direction of the cheaper good

  • Real Income effect: can be positive (normal) or negative *inferior)

  • Law of Demand/Demand curves slope downwards (Price effect) mostly because of the substitution effect

    • Even (inferior) goods with negative real income effects overpowered by substitution effect

  • Exception in the theoretical Giffen good: negative R.I.E. > S.E.

    • An upward sloping demand curve!

From Optimal Consumption Points to Demand

Demand Schedule

  • Demand schedule expresses the quantity of good a person would be willing to buy (qD) at any given price (px)

  • Note: each of these is a consumer's optimum at a given price!

price quantity
10 0
9 1
8 2
7 3
6 4
5 5
4 6
3 7
8 2
9 1
10 0

Demand Curve

  • Demand curve graphically represents the demand schedule

  • Also measures a person's maximum willingness to pay (WTP) for a given quantity

  • Law of Demand (price effect) ⟹ Demand curves always slope downwards

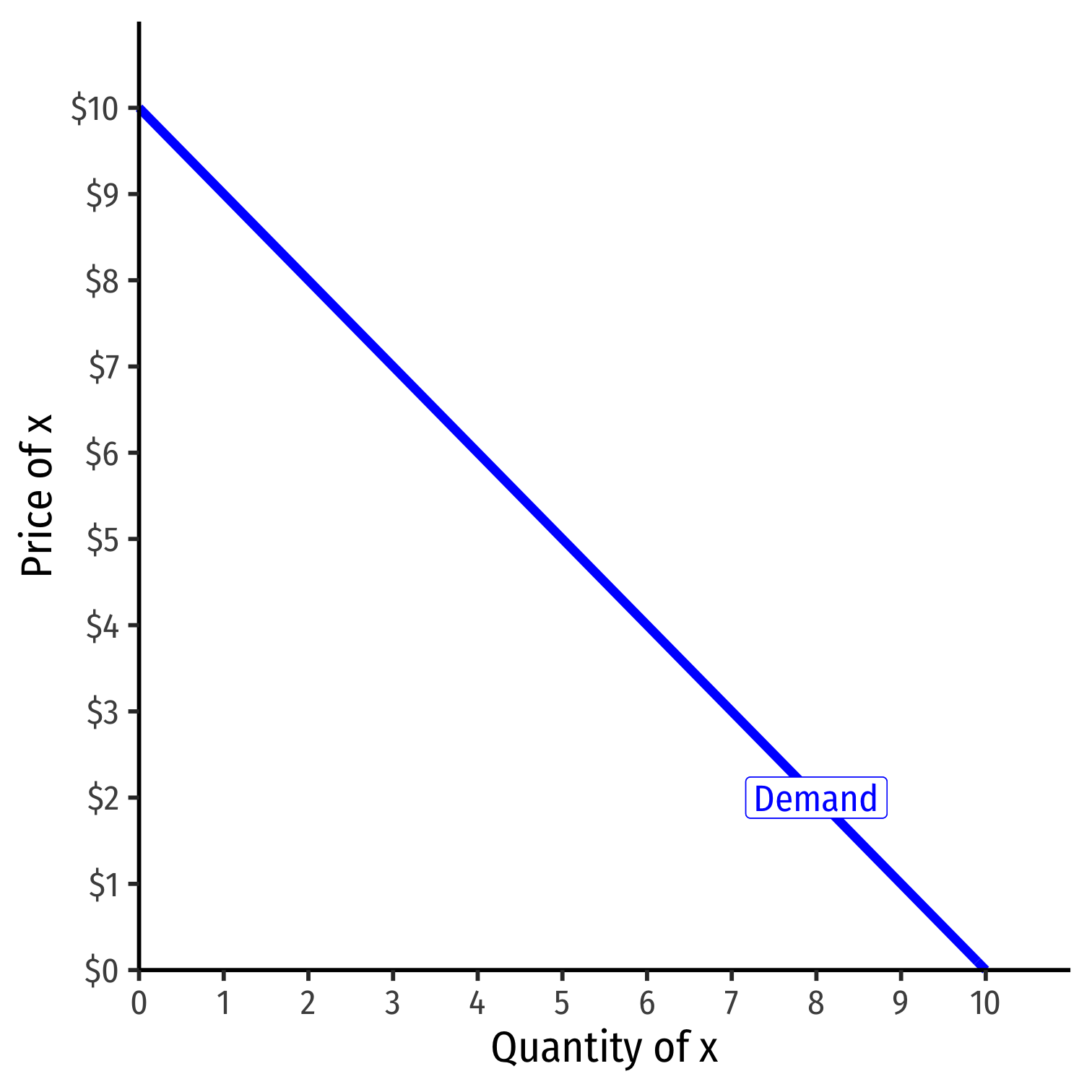
Demand Function

  • Demand function relates quantity to price

Example: q=10−p

  • Not graphable (wrong axes)!

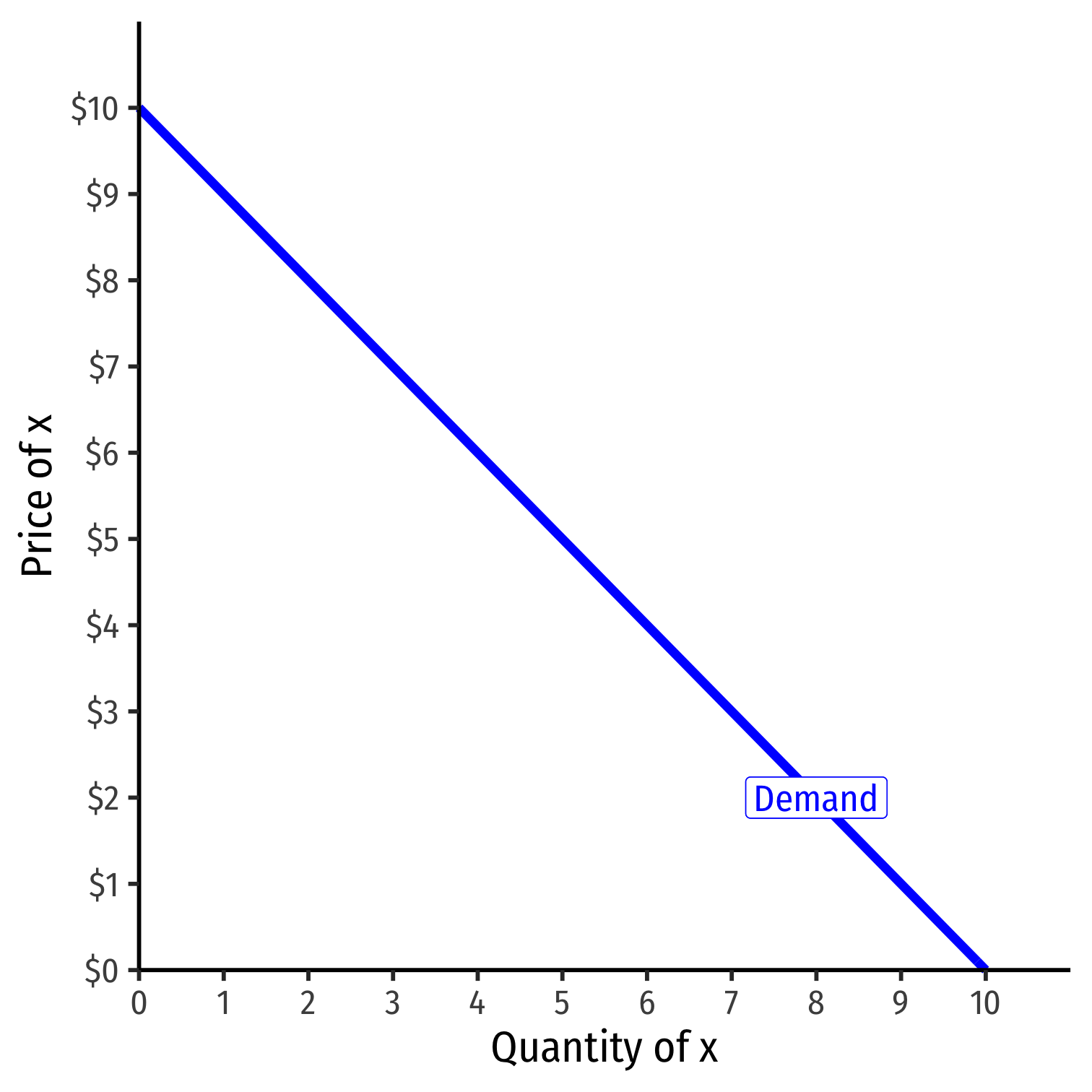
Inverse Demand Function

  • Inverse demand function relates price to quantity
    • Find by taking demand function and solving for p

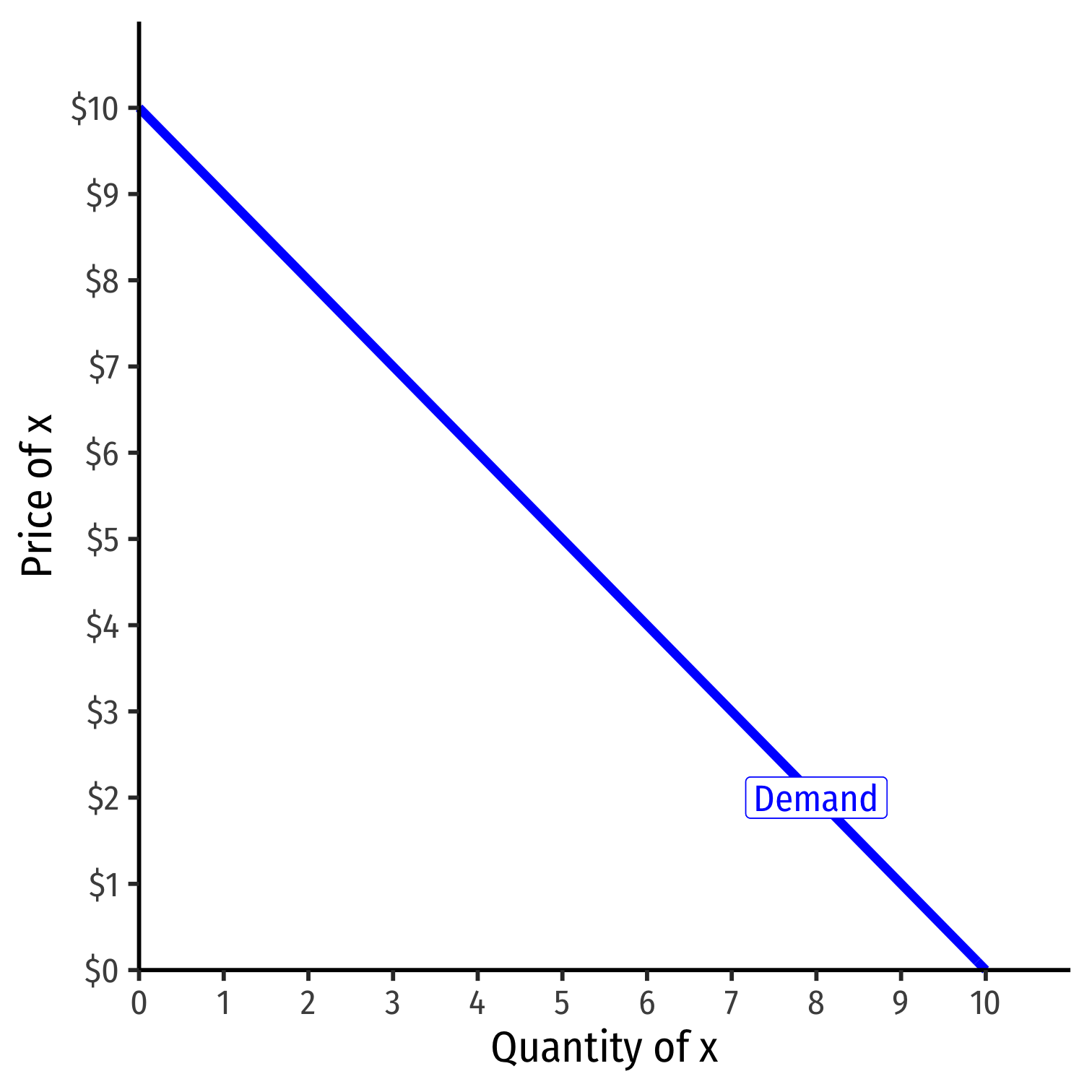
Example: p=10−q

  • Graphable (price on vertical axis)!

Inverse Demand Function

  • Inverse demand function relates price to quantity
    • Find by taking demand function and solving for p

Example: p=10−q

  • Graphable (price on vertical axis)!

  • Slope: −1

  • Vertical intercept called the "Choke price": price where qD=0 ($10), just high enough to discourage any purchases

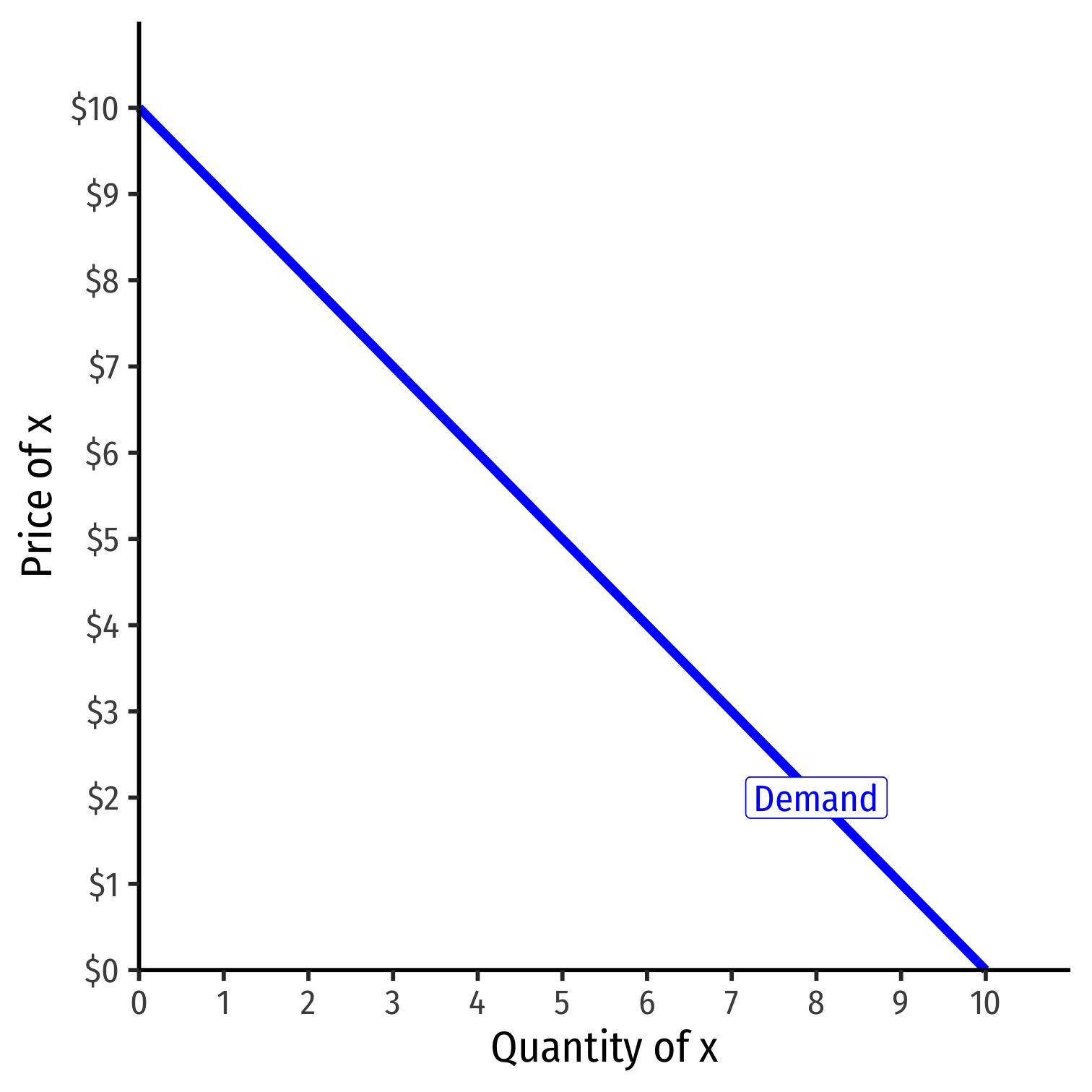
Inverse Demand Function

  • Inverse demand function relates price to quantity
    • Find by taking demand function and solving for p

Example: p=10−q

  • Read two ways:

  • Horizontally: at any given price, how many units person wants to buy

  • Vertically: at any given quantity, the maximum willingness to pay (WTP) for that quantity

    • This way will be very useful later

Deriving a Demand Curve Graphically

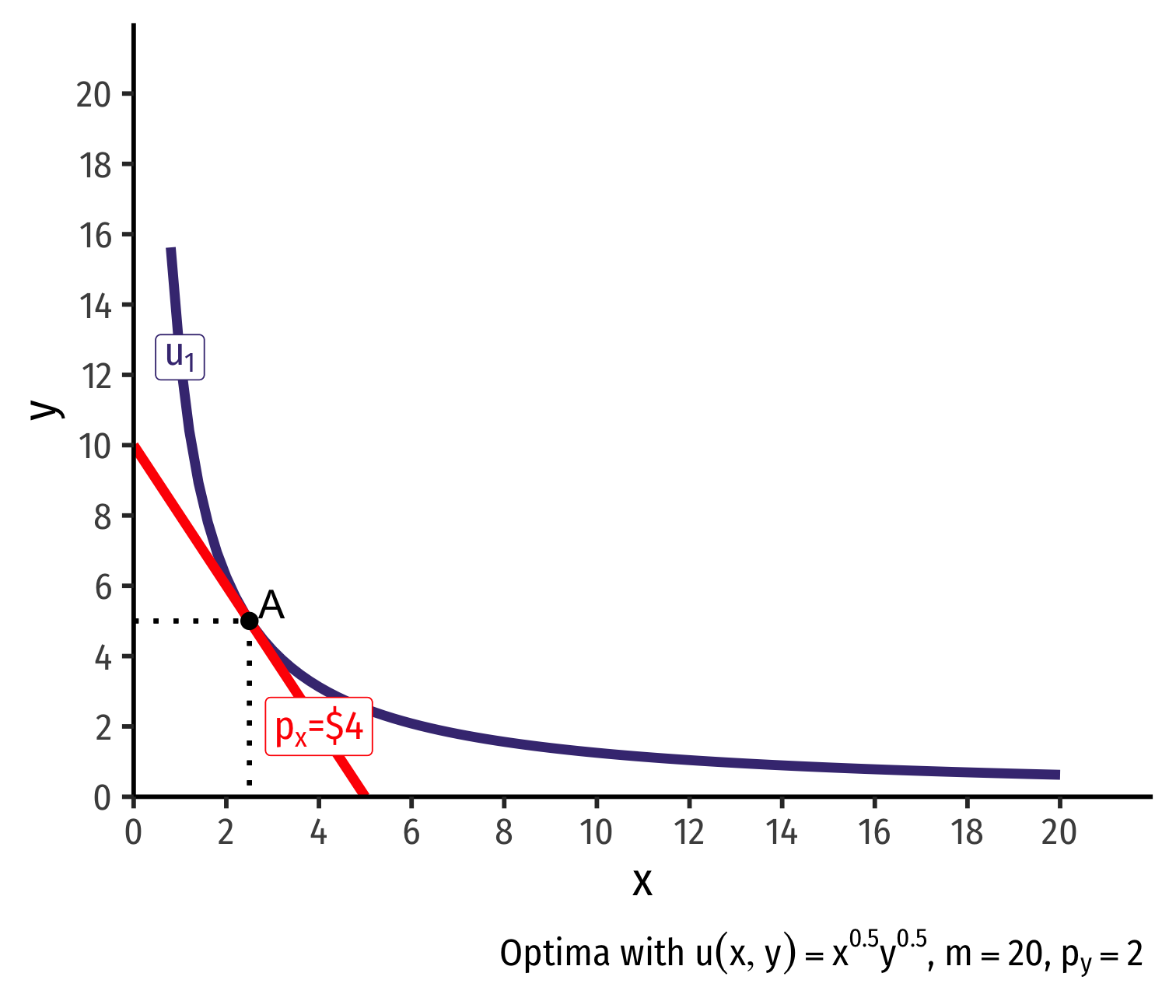
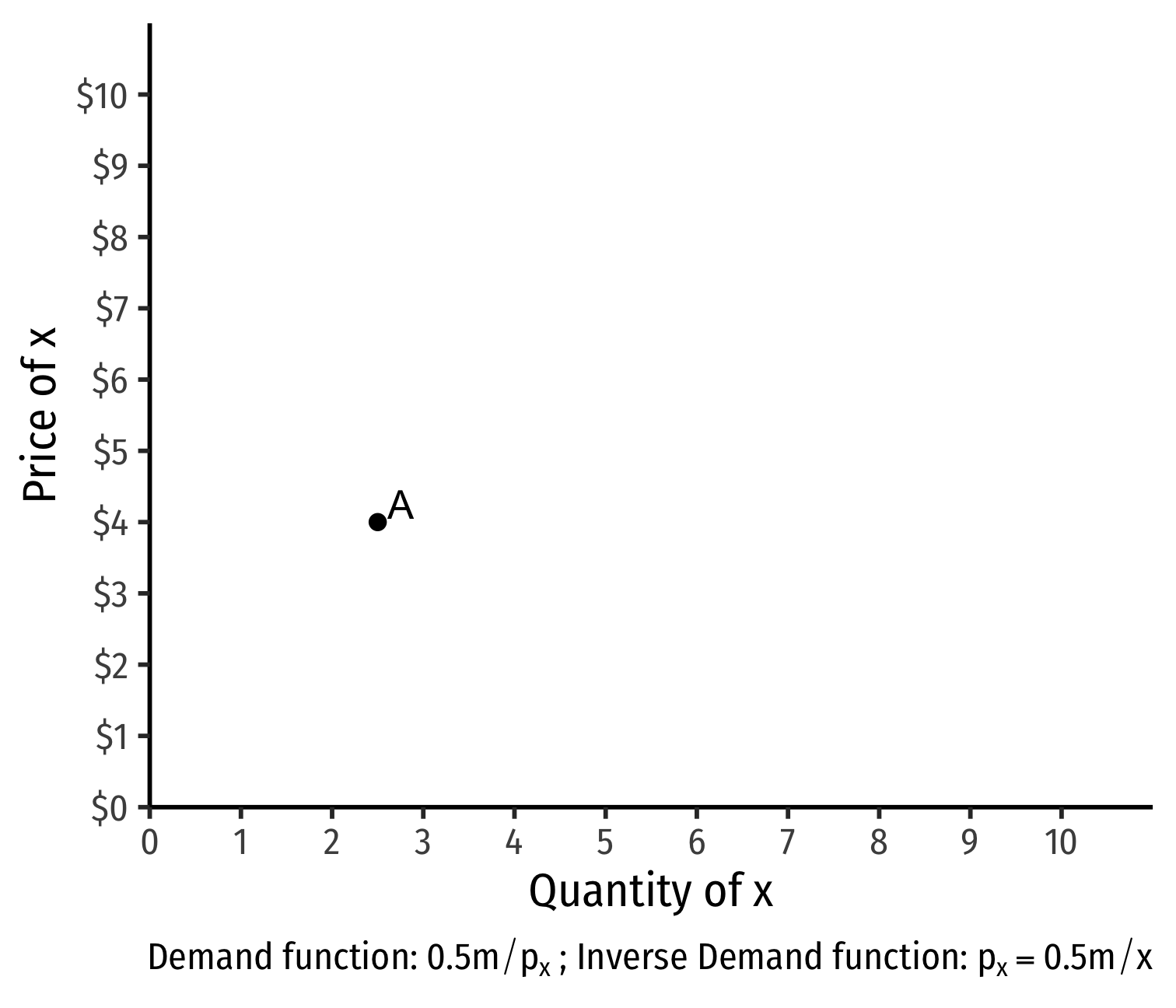
  • Demand curve for x relates consumer's optimal consumption of x ("quantity") as price of x changes
  • At px=4, consumer buys 2 x

Deriving a Demand Curve Graphically

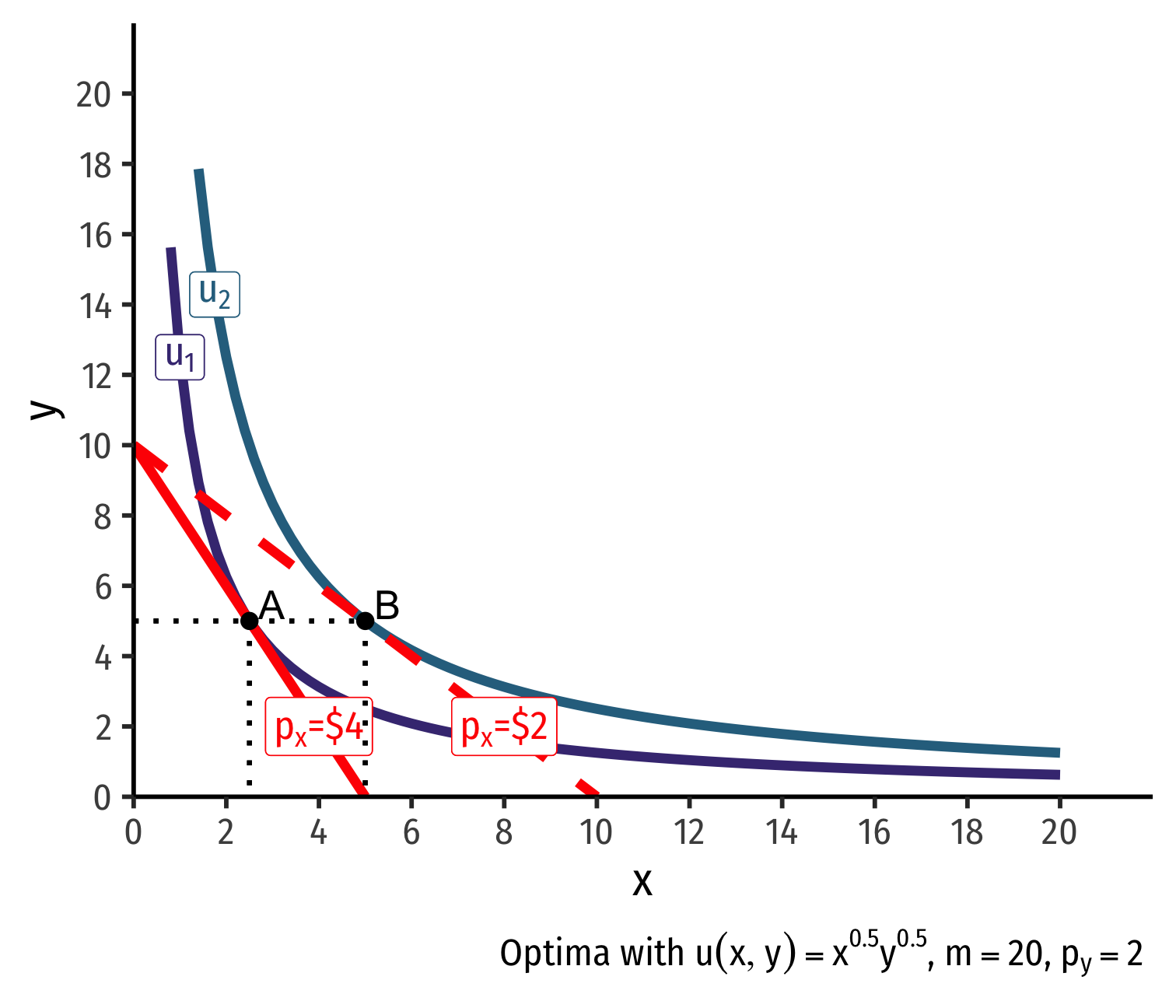
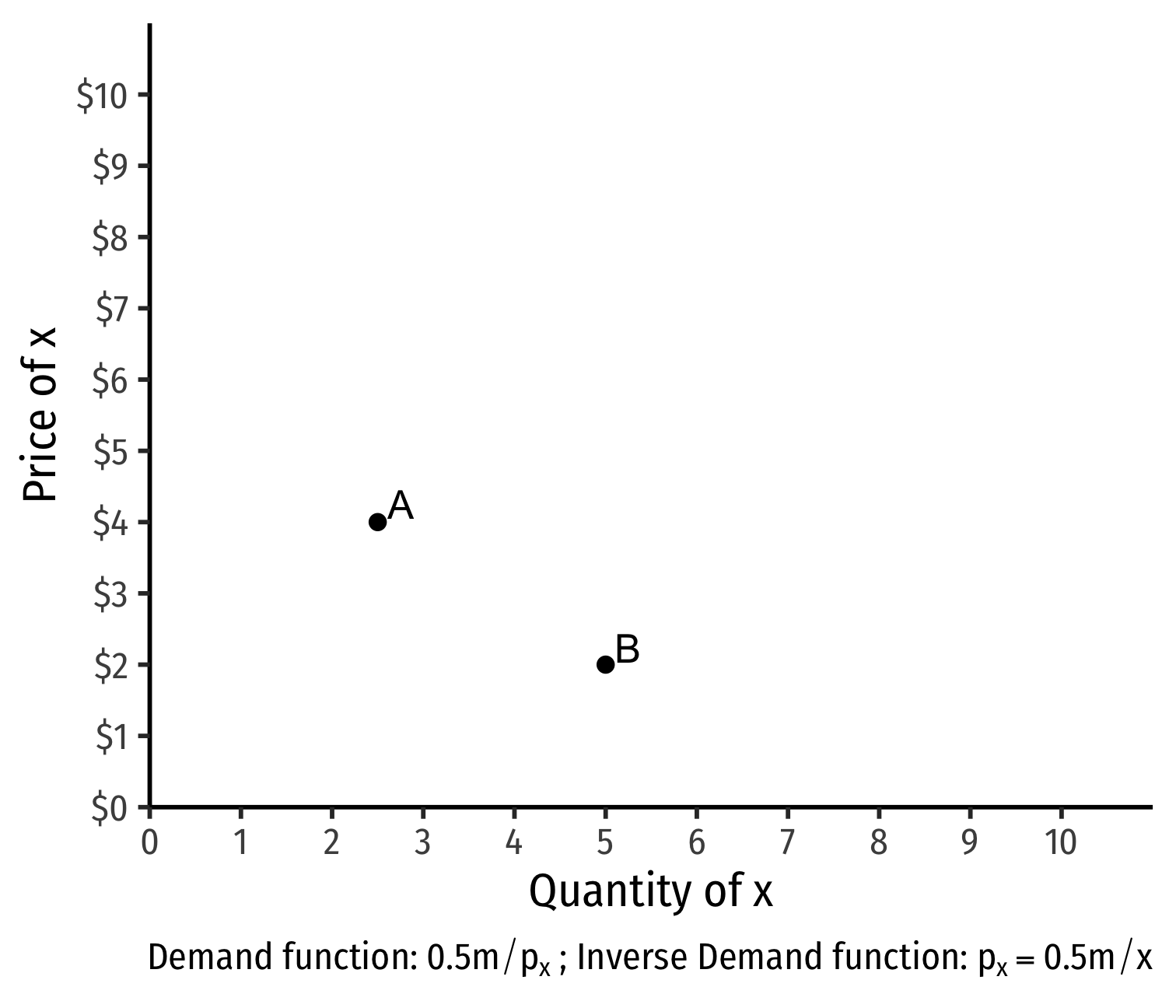
  • Demand curve for x relates consumer's optimal consumption of x ("quantity") as price of x changes
  • At px=4, consumer buys 2 x; at px=2, consumer buys 5 x

Deriving a Demand Curve Graphically

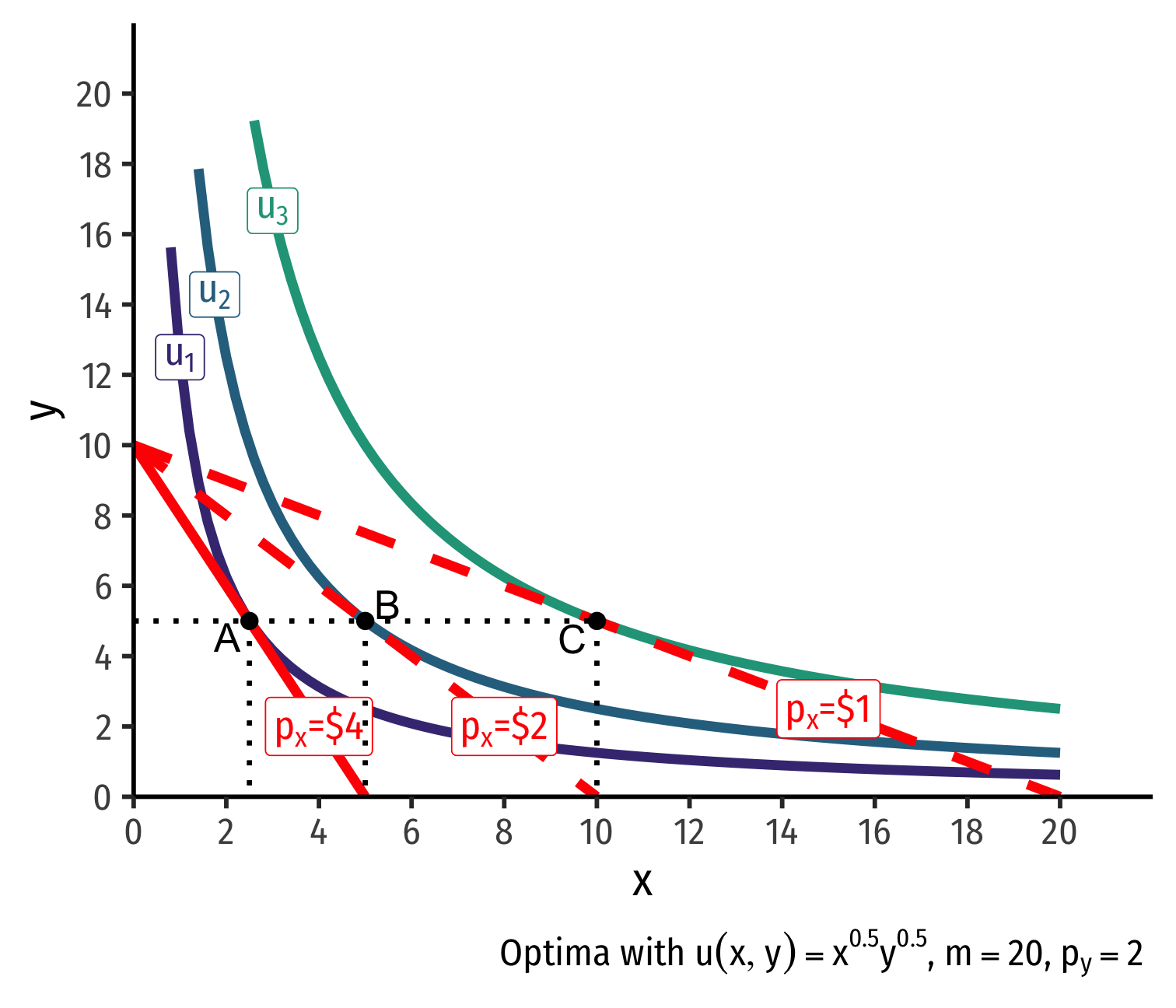
  • Demand curve for x relates consumer's optimal consumption of x ("quantity") as price of x changes
  • At px=4, consumer buys 2 x; at px=2, consumer buys 5 x; at px=1, consumer buys 10 x

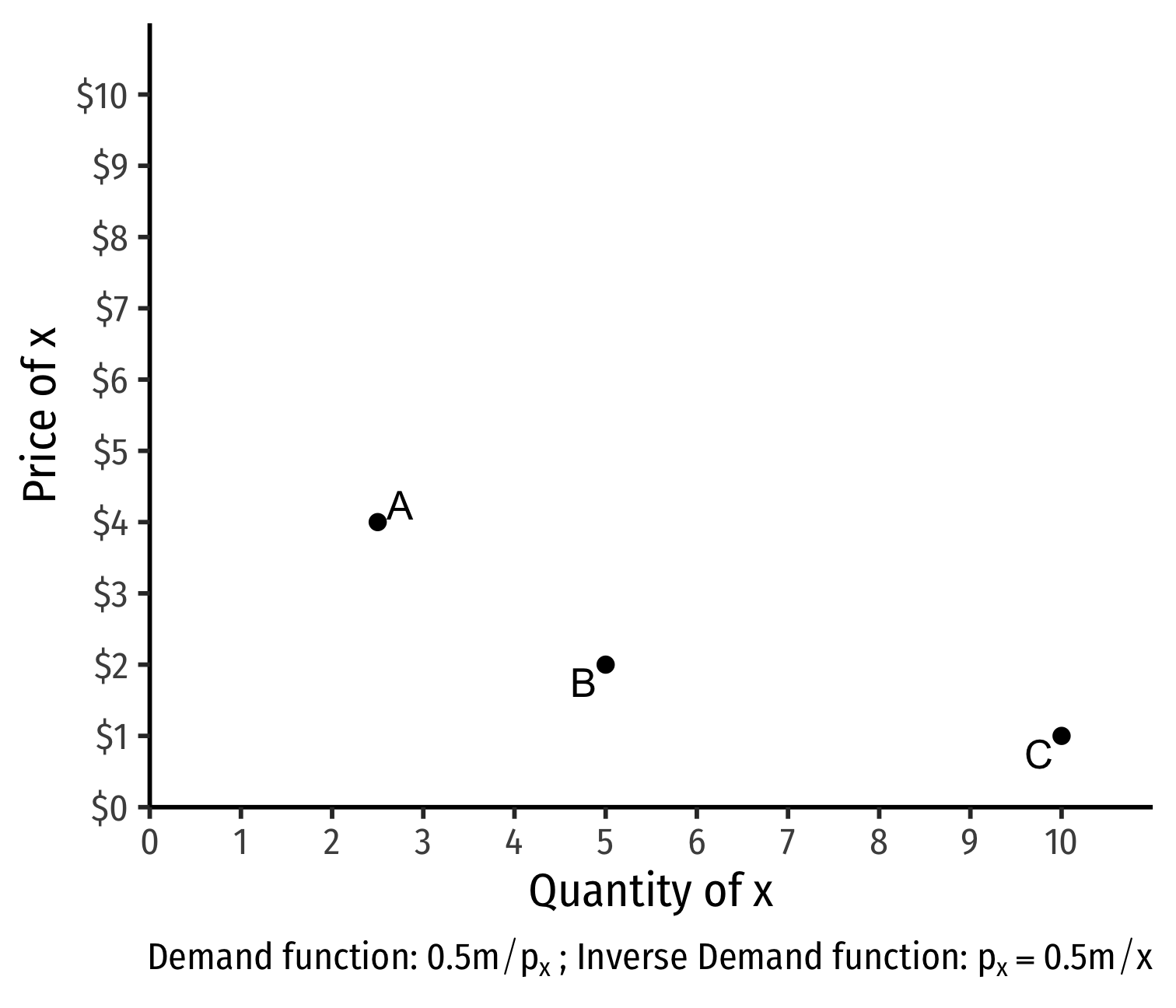
Deriving a Demand Curve Graphically

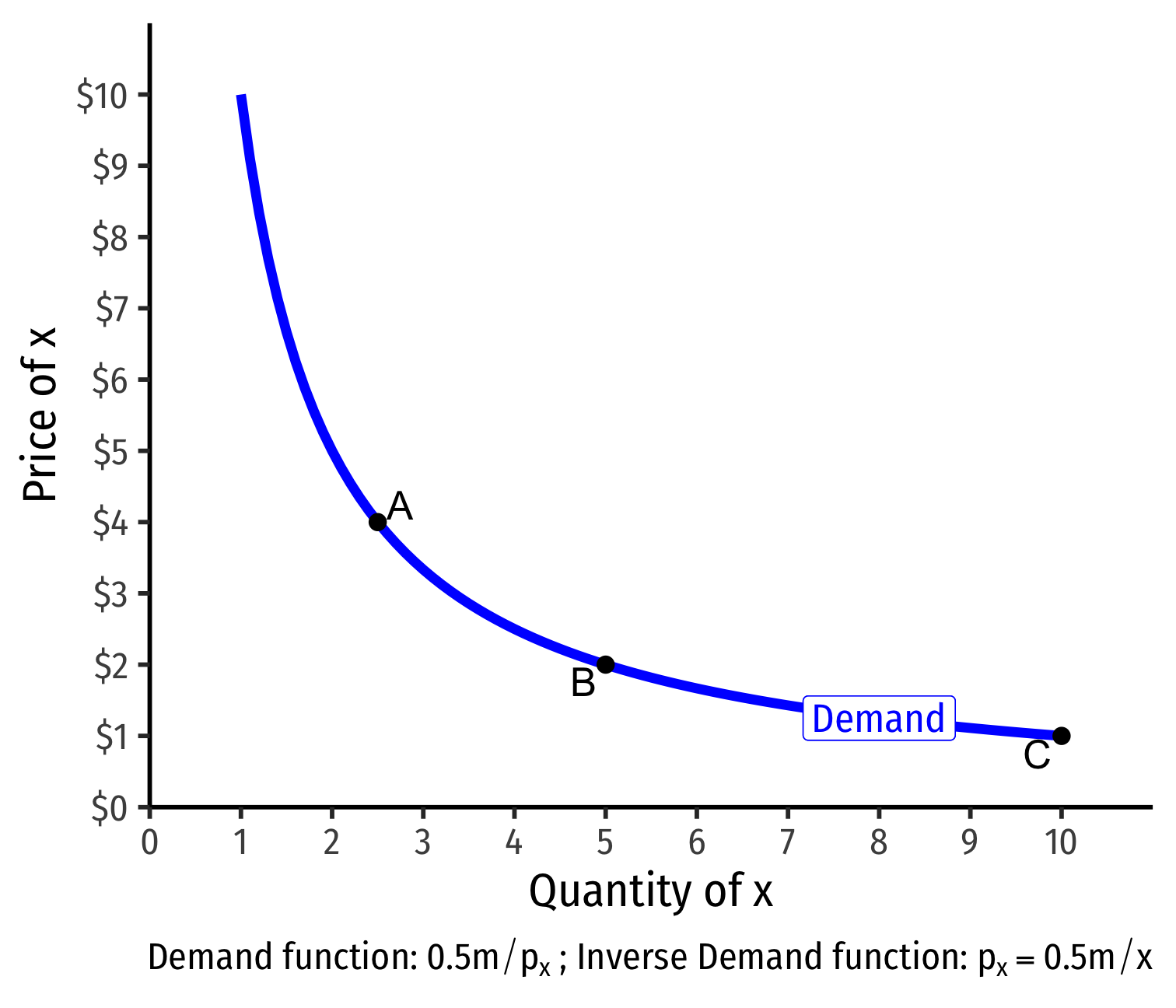
  • Demand curve for x relates consumer's optimal consumption of x ("quantity") as price of x changes
  • At px=4, consumer buys 2 x; at px=2, consumer buys 5 x; at px=1, consumer buys 10 x

Deriving a Demand Function I

  • I will always give you a (linear) demand function

  • Today's class notes page shows how you can derive actual demand functions from utility functions

Deriving a Demand Function II

MATH FYI: for a Cobb-Douglas utility function (where the two exponents sum to 1): u(x,y)=xay(1−a)

the demand function for x is qx=ampx

  • Property 1: Consumer always spends proportion a of their total income on x!

  • Ptroperty 2: demand for x is unaffected by prices of other goods (no py anywhere)!

  • To get a demand function just in terms of price, input a given income.

Deriving a Demand Function III

Example: u(x,y)=x0.5y0.5, demand function is

qx=0.5mpx

  • Always spend 50% (a) of income on x

  • With an income of m=10 Demand: qx=5pxInv. demand: px=5qx

  • With an income of m=50 Demand: qx=25pxInv. demand: px=25qx

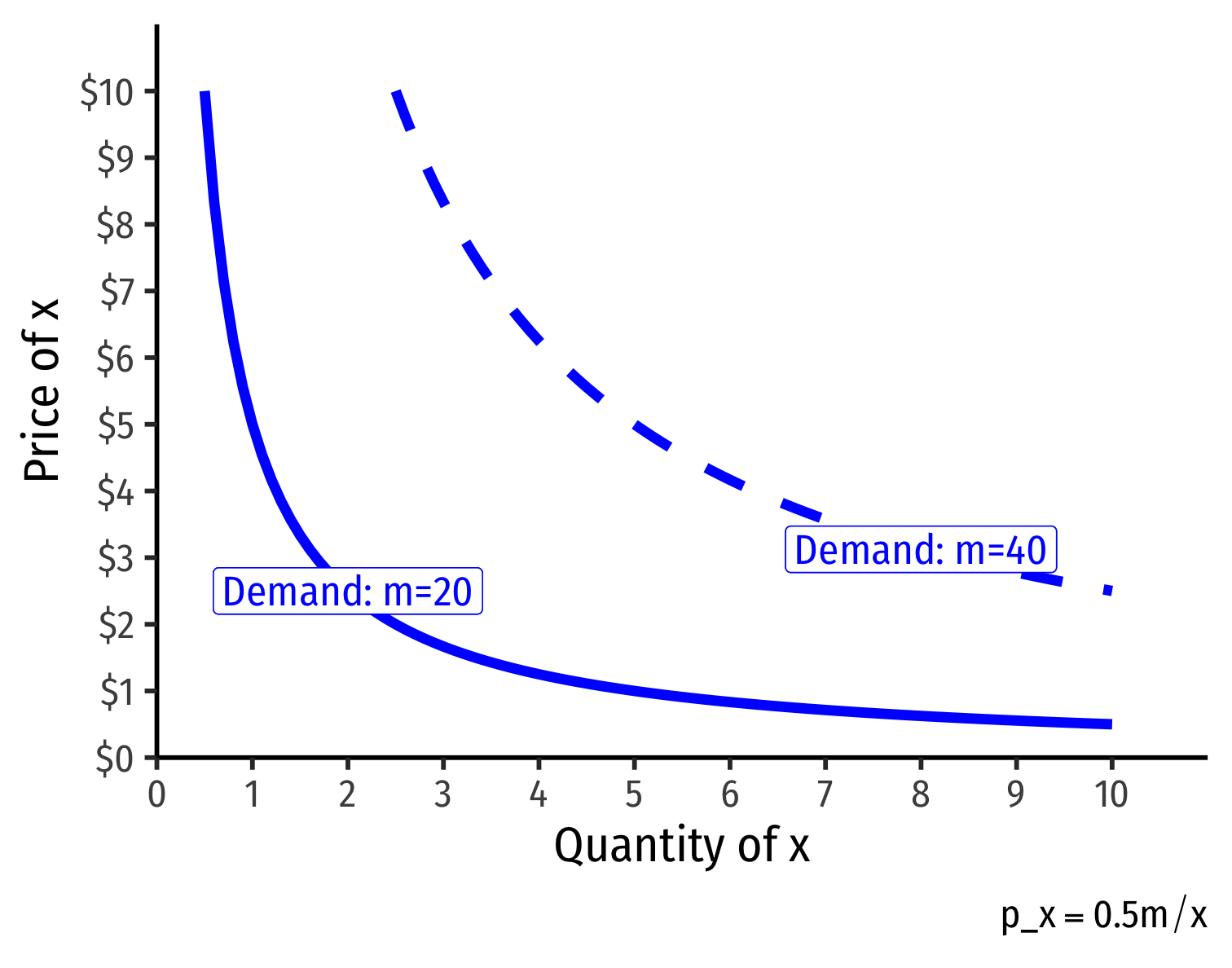
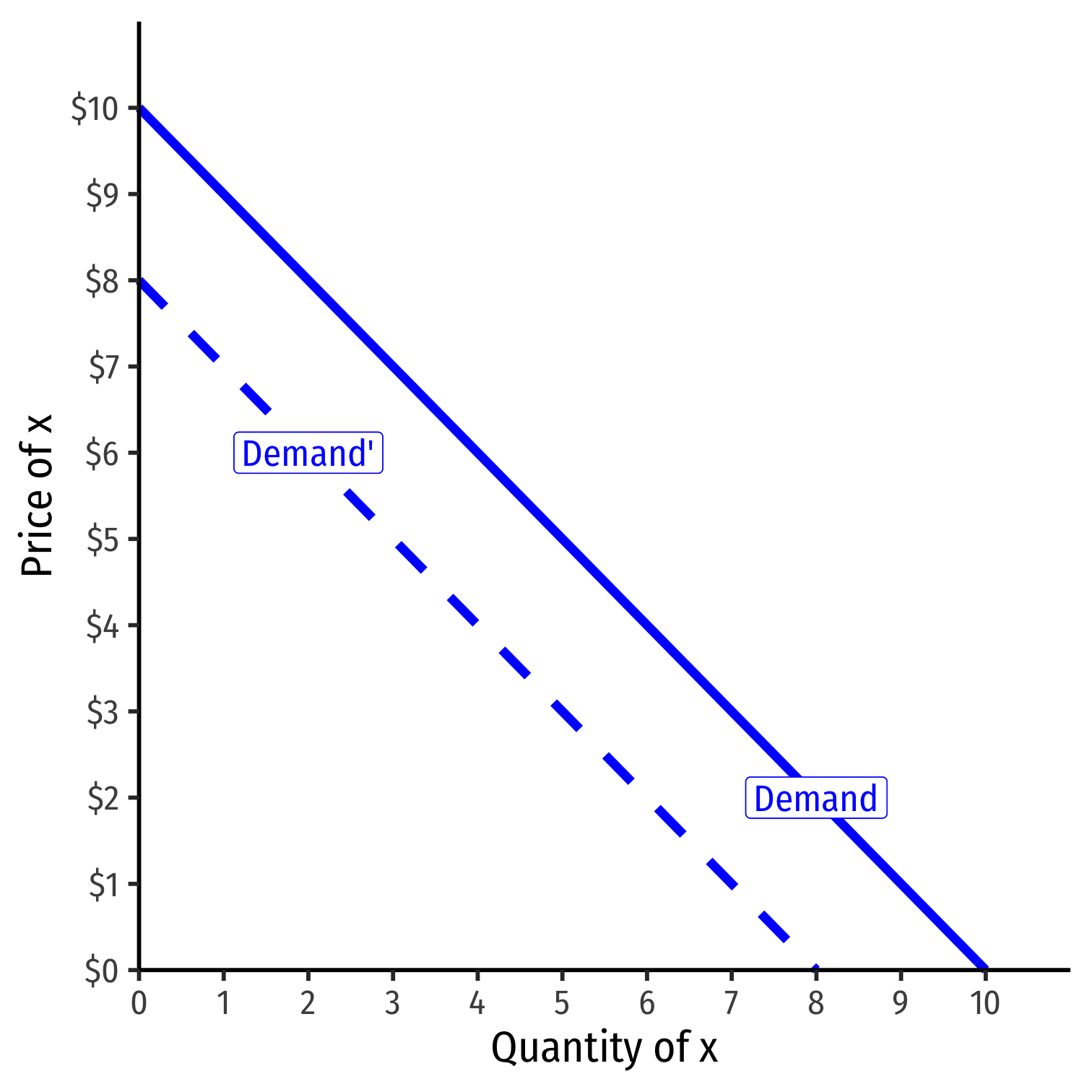
Shifts in Demand I

  • Note a simple (inverse) demand function only relates (own) price and quantity

Example: q=10−p or p=10−q

  • What about all the other "determinants of demand" like income and other prices?

  • They are captured in the vertical intercept (choke price)!

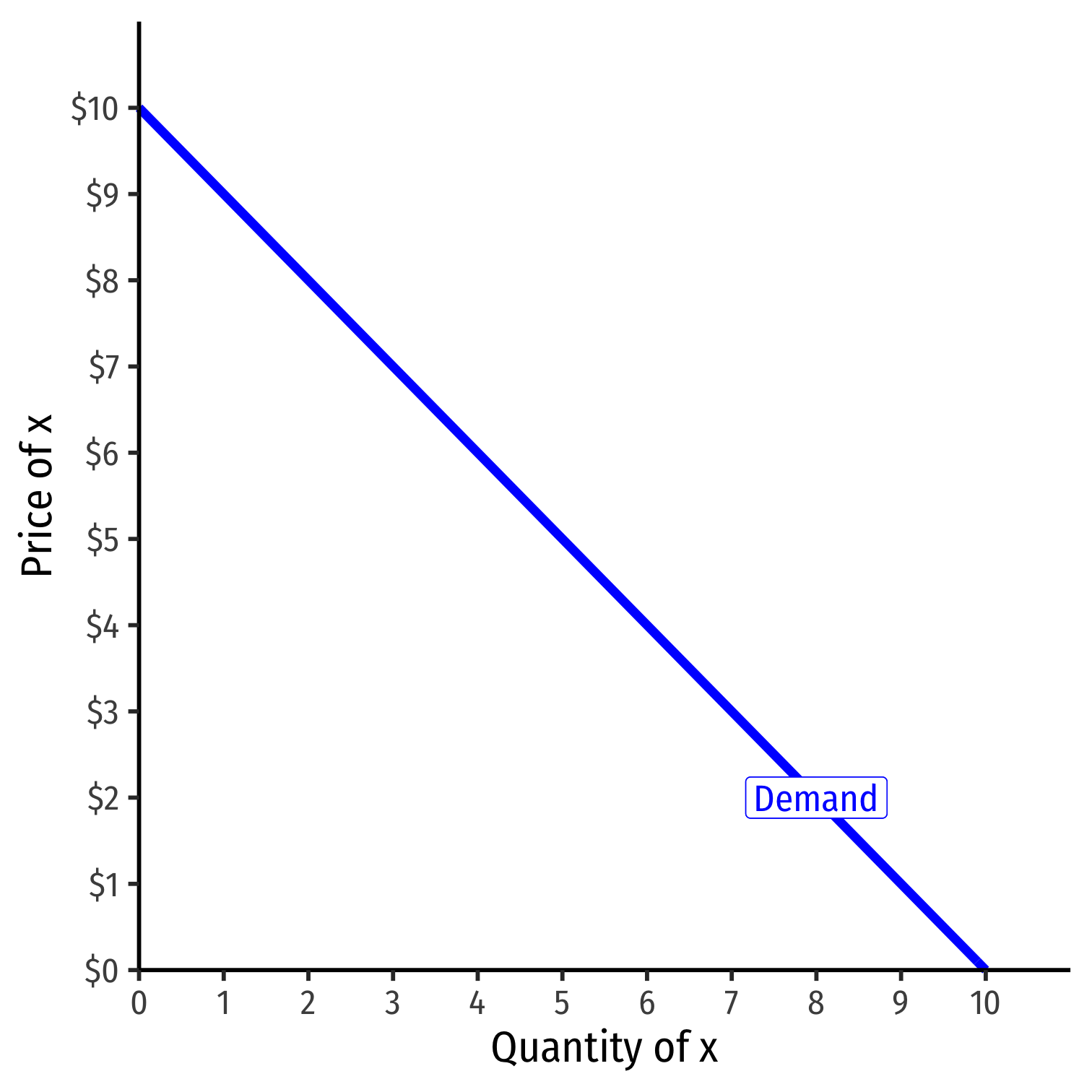
Shifts in Demand I

  • Note a simple (inverse) demand function only relates (own) price and quantity

Example: q=10−p or p=10−q

  • What about all the other "determinants of demand" like income and other prices?

  • They are captured in the vertical intercept (choke price)!

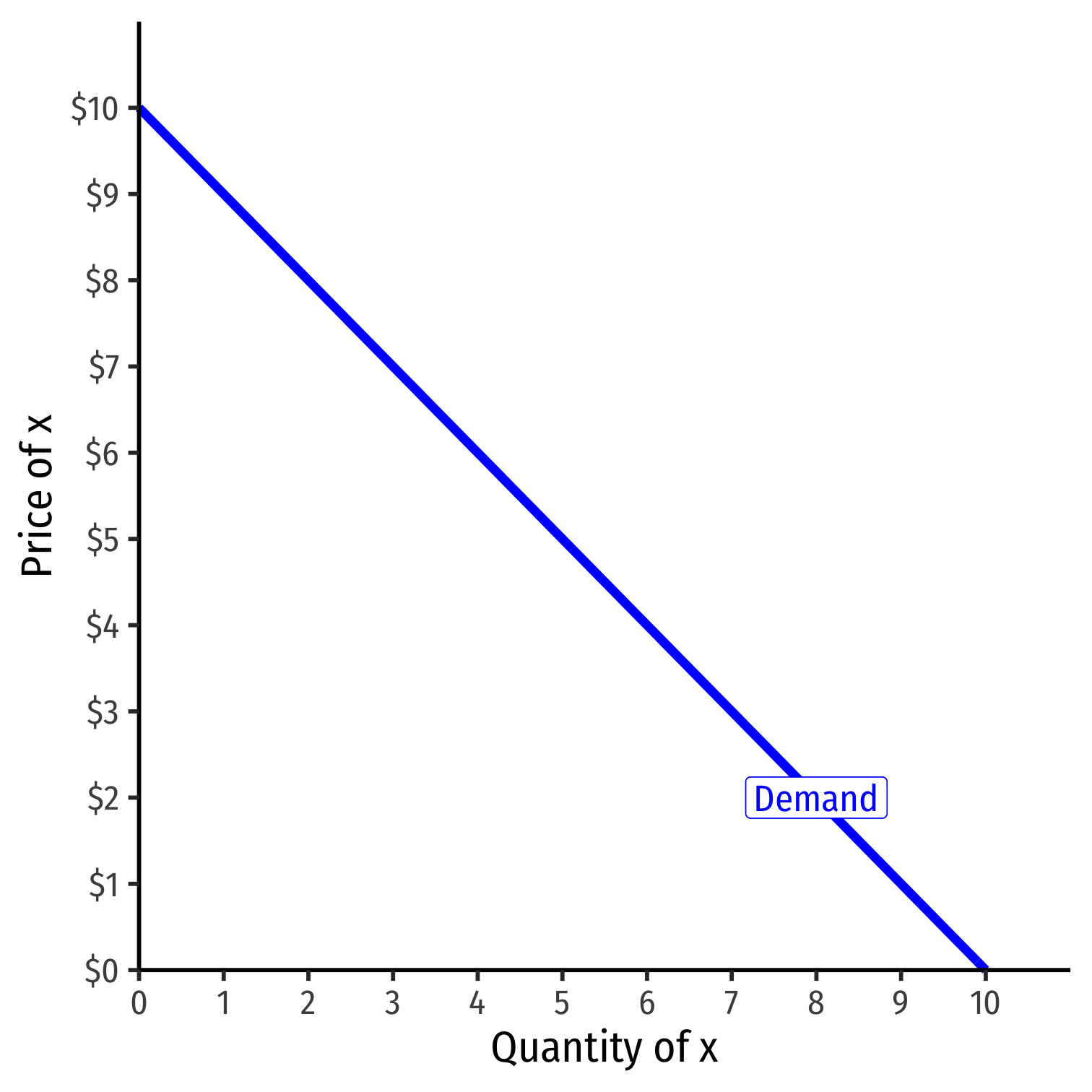
Shifts in Demand II

  • A change in one of the "determinants of demand" (or "shifters") will shift the demand curve

    • Change in income m
    • Change in price of other goods py (substitutes or complements)
    • Change in preferences or expectations about good x (show up in utility function)
    • Change in number of buyers in market

  • Shows up in (inverse) demand function by a change in the intercept (choke price)!

  • See my Visualizing Demand Shifters

A Demand Function (Again)

  • A consumer's quantity demanded (of good x), qDx is a function of their demand for good x, which depends on current market prices and their income

qDx=D(m,px,py)

  • We now want to examine how quantity demanded for x changes as each of these parameters change:
  1. Income effects (ΔqDxΔm): how qDx changes with changes in income
  2. Cross-price effects (ΔqDxΔpy): how qDx changes with changes in prices of other goods (e.g. y)
  3. (Own) Price effects (ΔqDxΔpx): how qDx changes with changes in price (of x)

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow