1.5: Preferences II: MRS and Utility Functions
ECON 306 · Microeconomic Analysis · Fall 2019
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microf19
microF19.classes.ryansafner.com
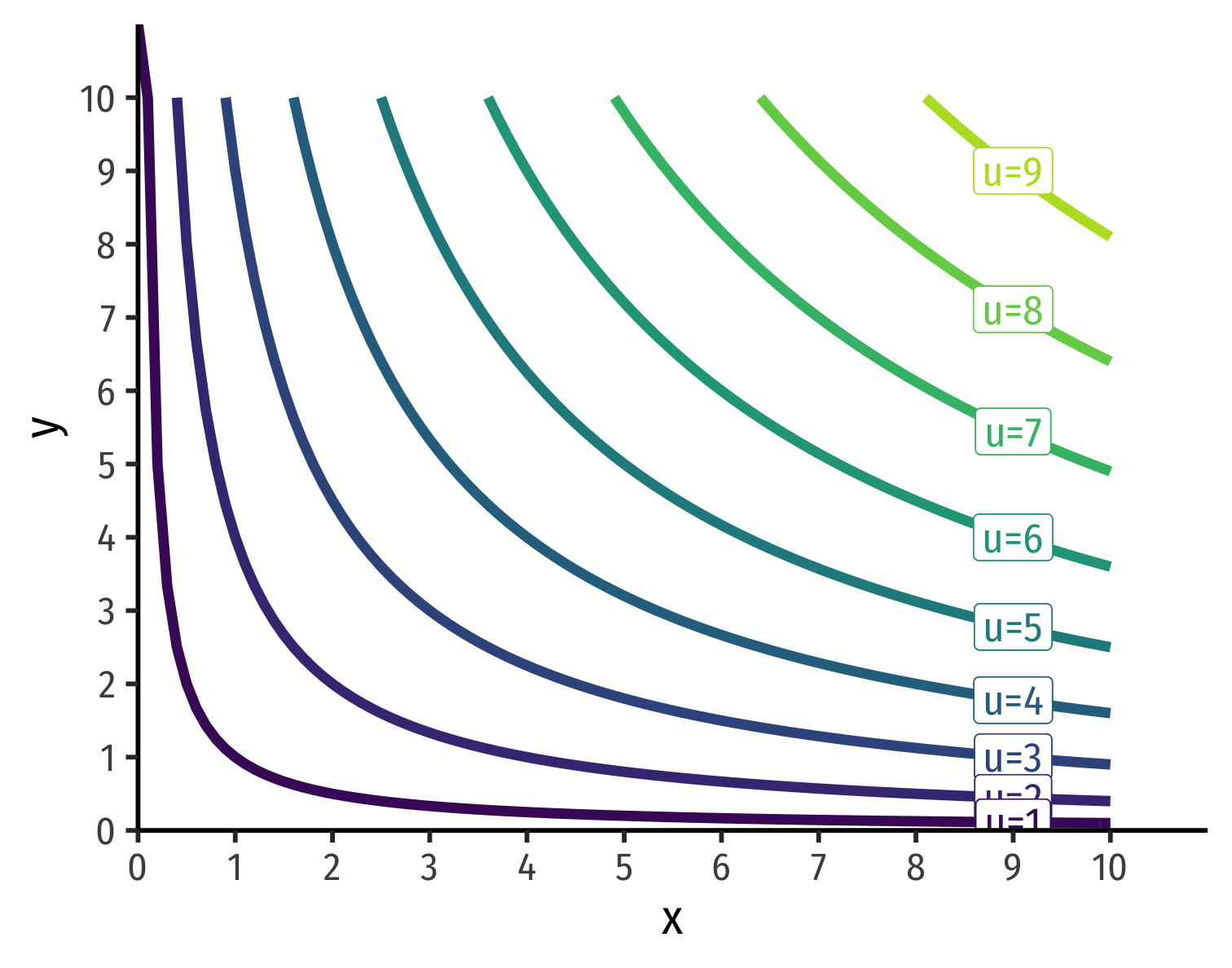
Utility Functions and Indifference Curves I
Two tools to represent preferences: indifference curves and utility functions
Indifference curve: all equally preferred bundles ⟺ same utility level
Each indifference curve represents one level (or contour) of utility surface (function)

Marginal Utility
MRS and Marginal Utility I
Recall: marginal rate of substitution MRSx,y is the slope of the indifference curve
- Rate at which y is given up for 1 more x
It would be handy to be able to calculate MRS
- Recall it changes (a curve, not a straxfight line)!
- We can calculate it using something from the utility function
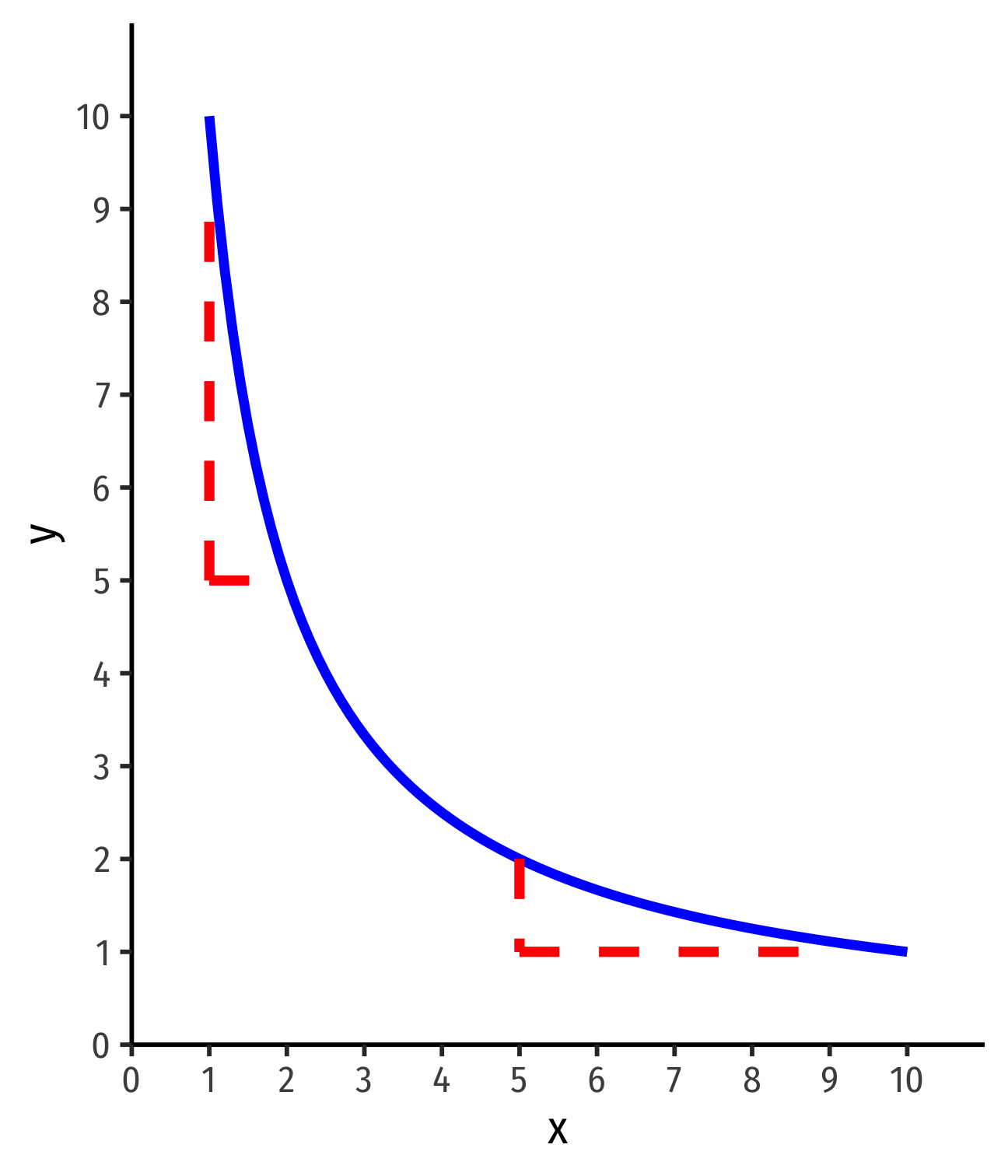
MRS and Marginal Utility II
- Marginal utility: change in (total) utility from a one-unit increase in consumption of a good
MRS and Marginal Utility II
- Marginal utility: change in (total) utility from a one-unit increase in consumption of a good
Marginal utility of x: MUx=Δu(x,y)Δx
MRS and Marginal Utility II
- Marginal utility: change in (total) utility from a one-unit increase in consumption of a good
Marginal utility of x: MUx=Δu(x,y)Δx
Marginal utility of y: MUy=Δu(x,y)Δy
MRS and Marginal Utility II
- Marginal utility: change in (total) utility from a one-unit increase in consumption of a good
Marginal utility of x: MUx=Δu(x,y)Δx
Marginal utility of y: MUy=Δu(x,y)Δy
- Math (calculus): "marginal" means "derivative with respect to"
- I will always derive marginal utility functions for you
MRS and Marginal Utility: Example
Example: For an example utility function
u(x,y)=x2+y3
- Marginal utility of x: MUx=2x
- Marginal utlity of y: MUy=3y
MRS and Marginal Utility III
How to relate MU and MRS?
Moving along an indifference curve
- X and Y will change
- MUx and MUy will change
- Utility is constant (Δu=0)
MRS and Marginal Utility IV
How to relate MU and MRS?
Moving along an indifference curve
- X and Y will change
- MUx and MUy will change
- Utility is constant (Δu=0)
MUxΔx+MUyΔy=Δu
MRS and Marginal Utility IV
How to relate MU and MRS?
Moving along an indifference curve
- X and Y will change
- MUx and MUy will change
- Utility is constant (Δu=0)
MUxΔx+MUyΔy=ΔuMUxΔx+MUyΔy=0
MRS and Marginal Utility IV
How to relate MU and MRS?
Moving along an indifference curve
- X and Y will change
- MUx and MUy will change
- Utility is constant (Δu=0)
MUxΔx+MUyΔy=ΔuMUxΔx+MUyΔy=0MUyΔy=−MUxΔx
MRS and Marginal Utility IV
How to relate MU and MRS?
Moving along an indifference curve
- X and Y will change
- MUx and MUy will change
- Utility is constant (Δu=0)
MUxΔx+MUyΔy=ΔuMUxΔx+MUyΔy=0MUyΔy=−MUxΔxΔyΔx⏟MRS=−MUxMUy
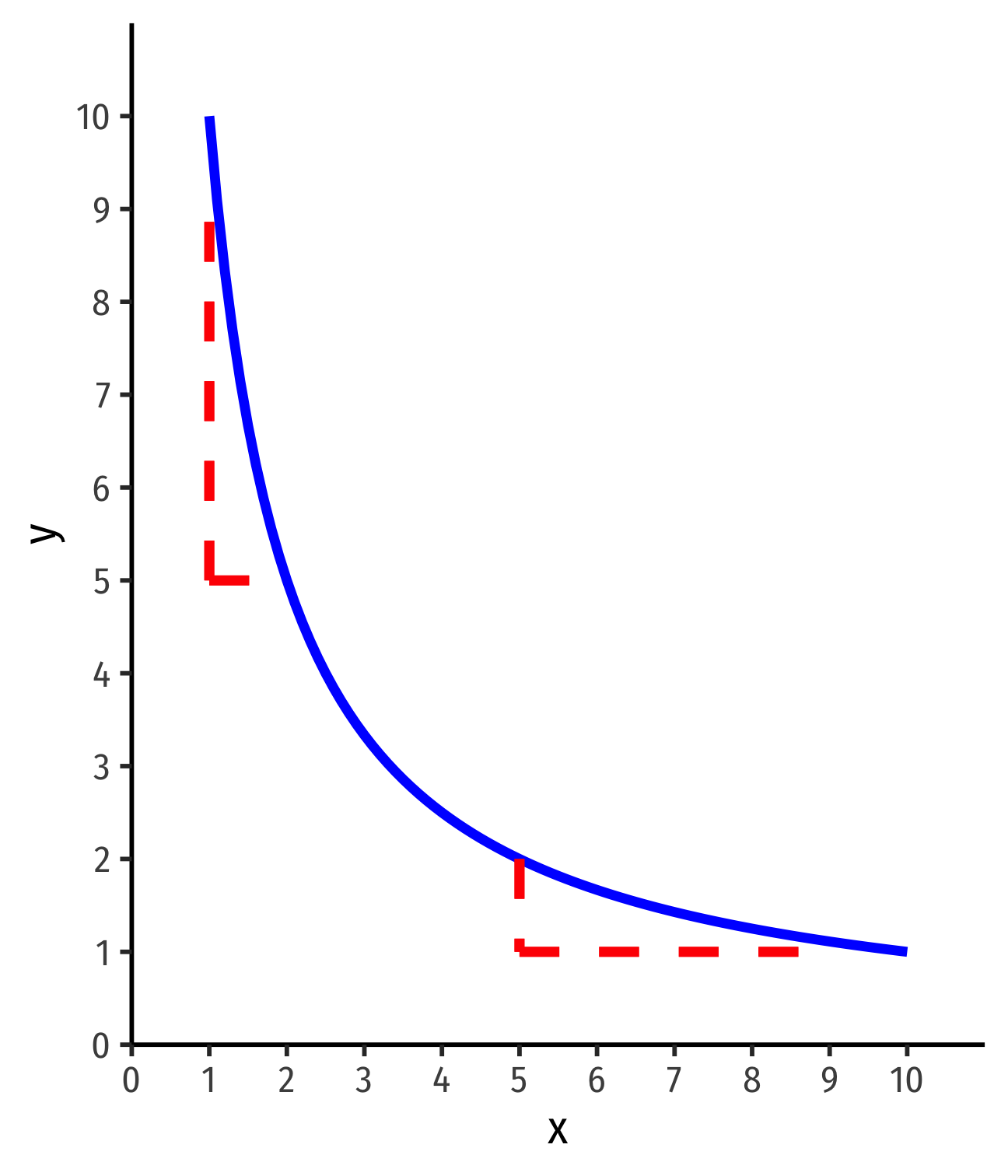
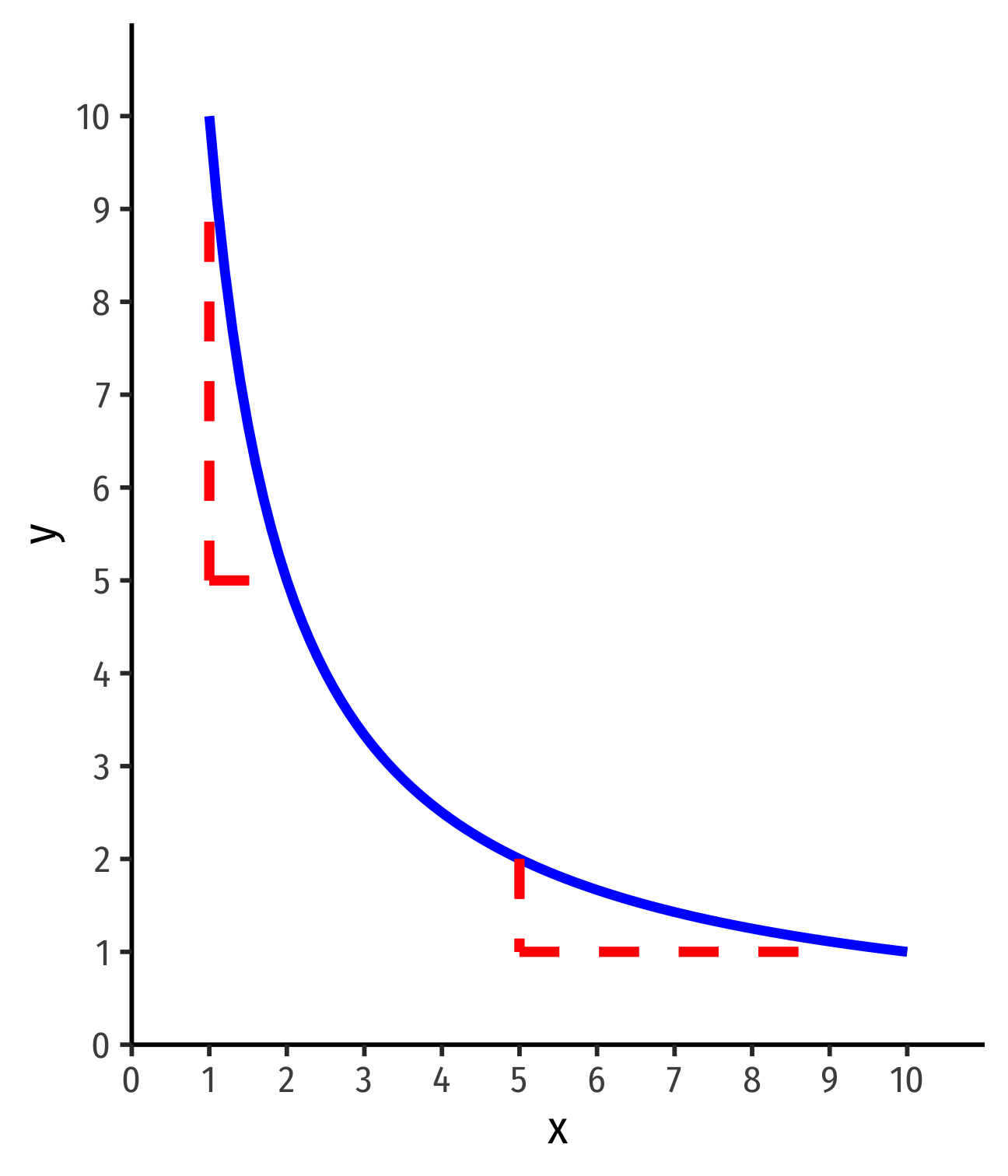
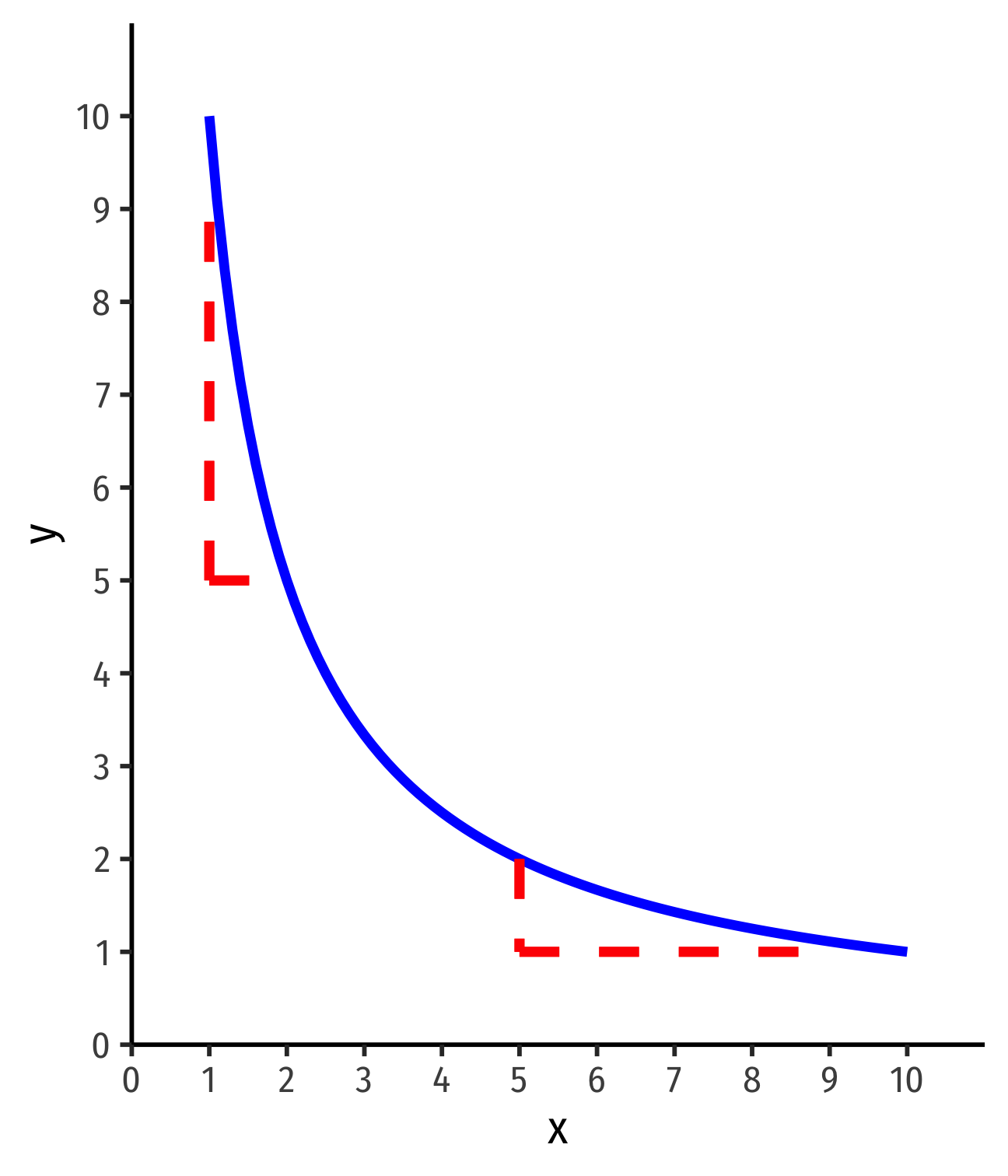
MRS and Preferences
MRS and Preferences
MRS=ΔyΔx⏟slope=−MUxMUy
Observing the choices that consumers make, given their options, give us insight into their preferences
Represented in indifference curves and MRS
Steepness of indifference curves tells us how consumers trade off between goods
Let's look at extremes first
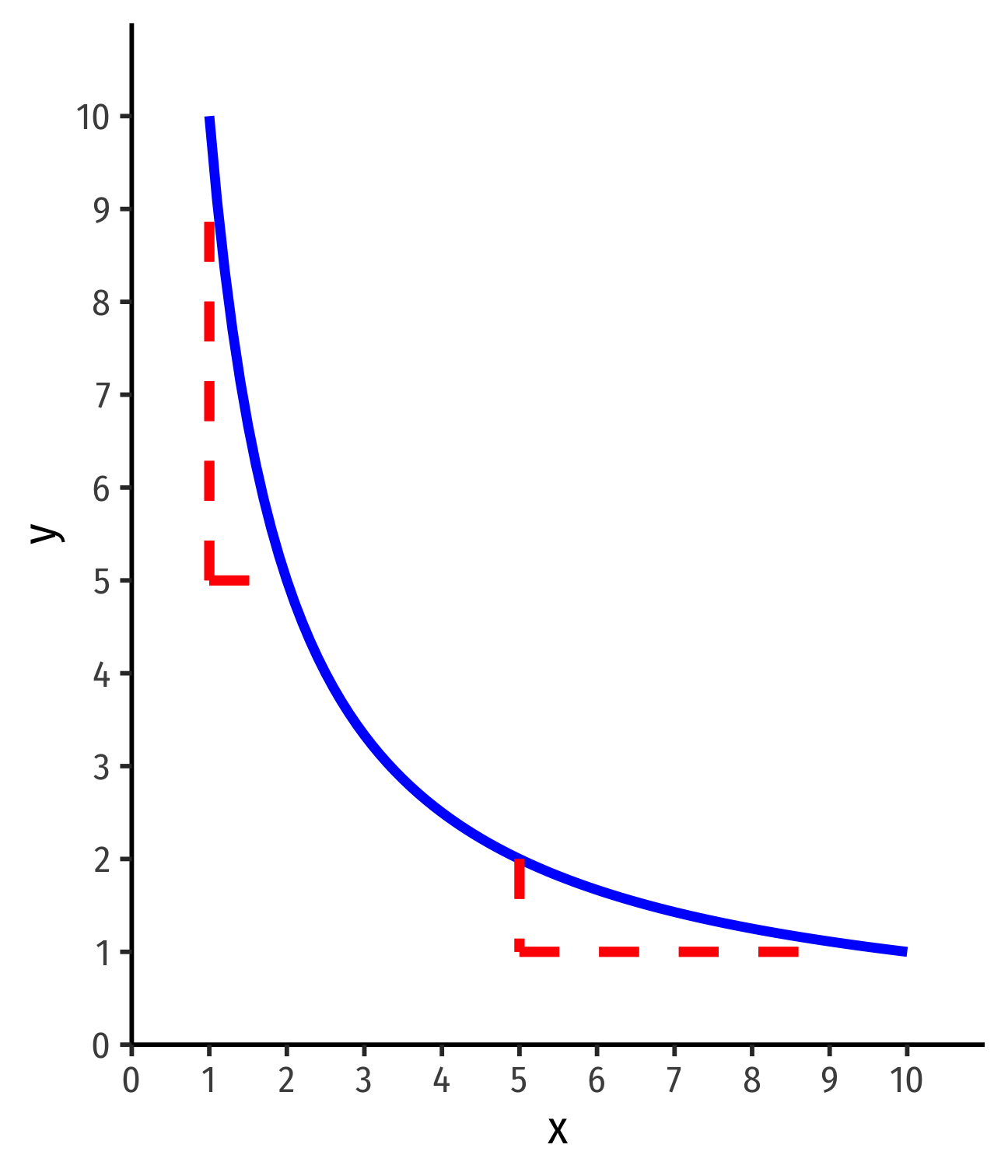
MRS and Preferences: Steepness I
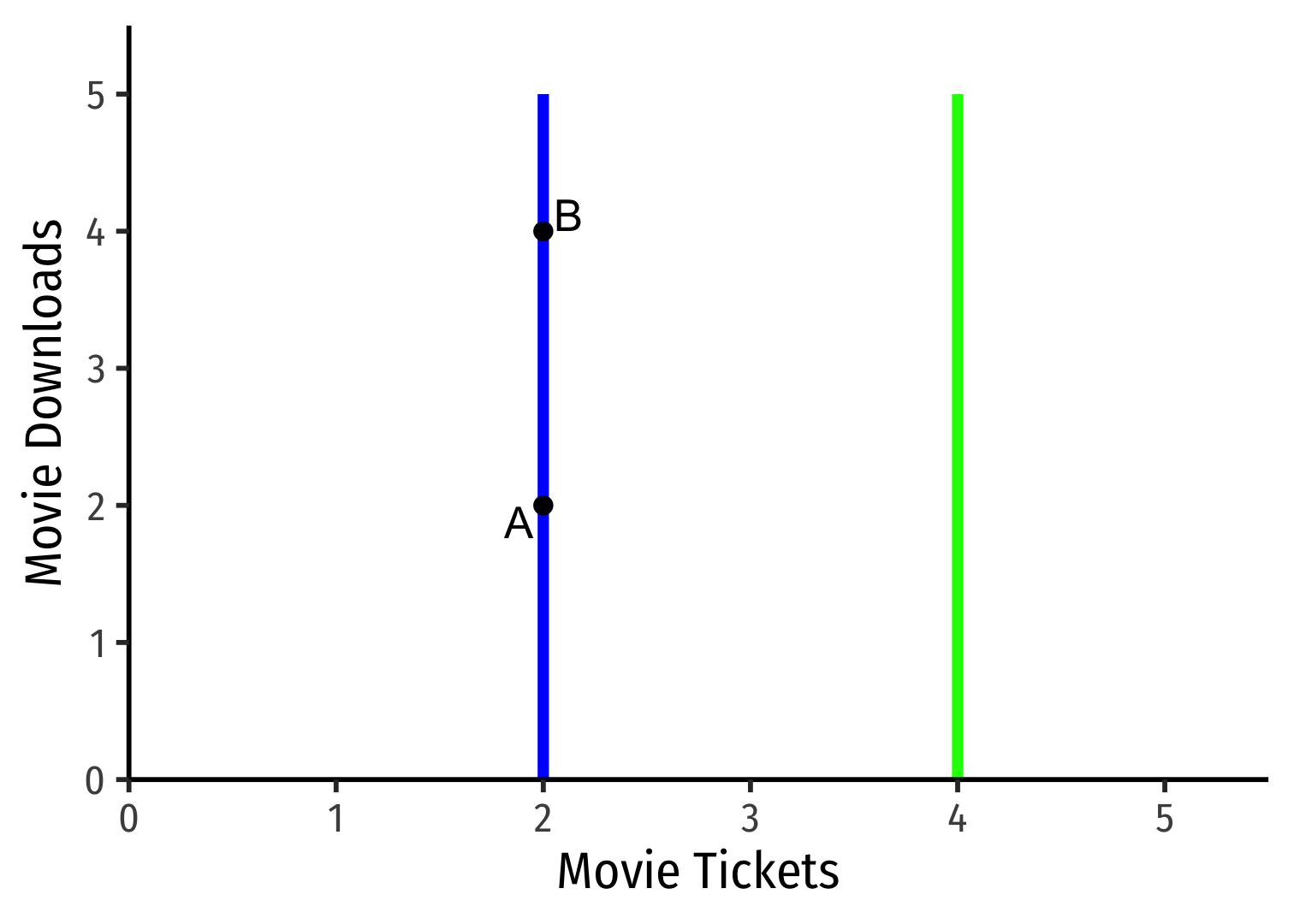
- Vertical curves ⟹ indifference between having more or less Downloads
- Downloads are a neutral (neither good nor bad)
- MRST,D=∞; give up ∞ (or undefined) Downloads to get more Tickets
MRS and Preferences: Steepness I

- Vertical curves ⟹ indifference between having more or less Downloads
- Downloads are a neutral (neither good nor bad)
- MRST,D=∞; give up ∞ (or undefined) Downloads to get more Tickets
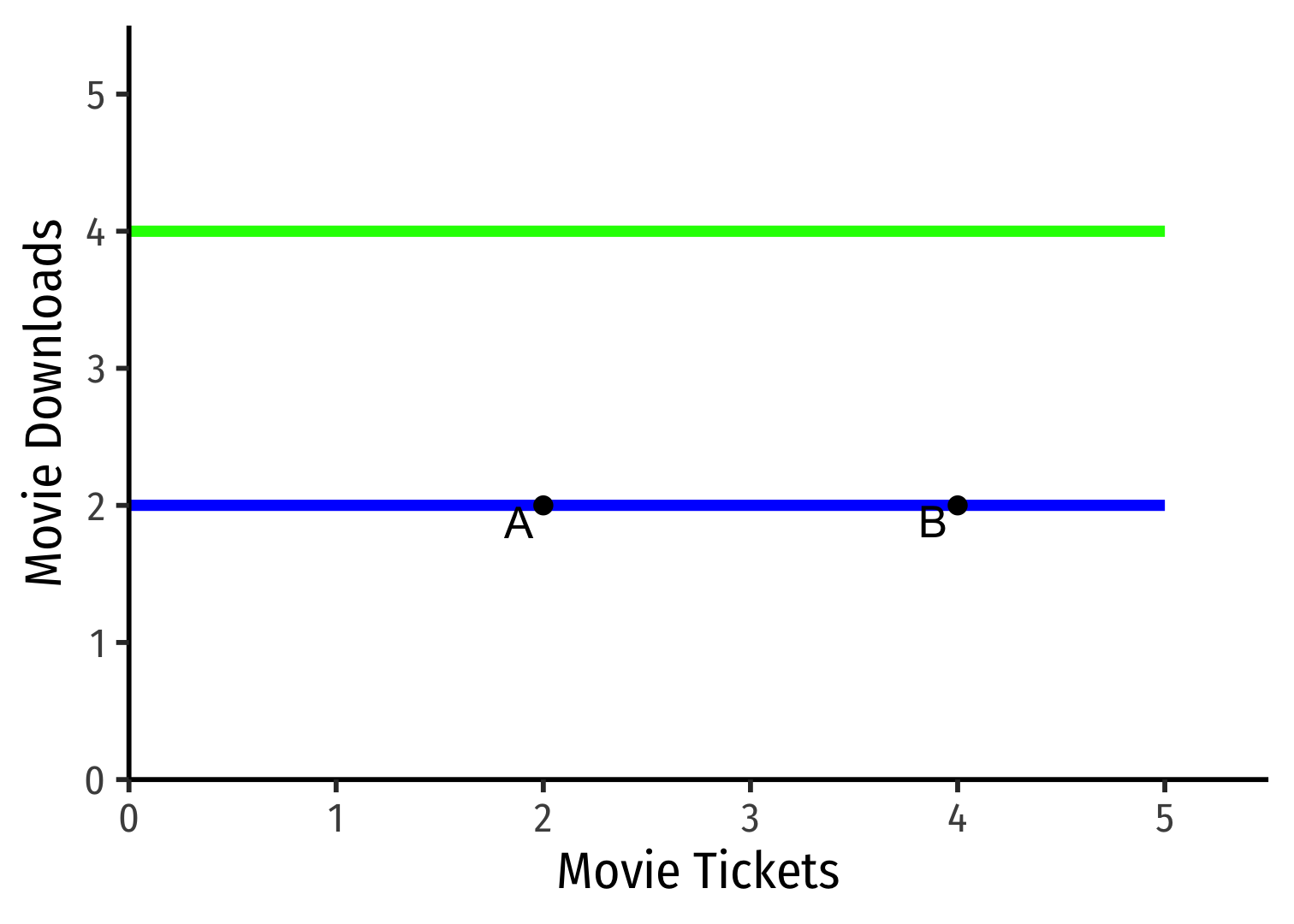
- Horizontal curves ⟹ indifference between having more or less Tickets
- Tickets are a neutral (neither good nor bad)
- MRST,D=0; give up 0 Downloads to get more Tickets
MRS and Preferences: Steepness II
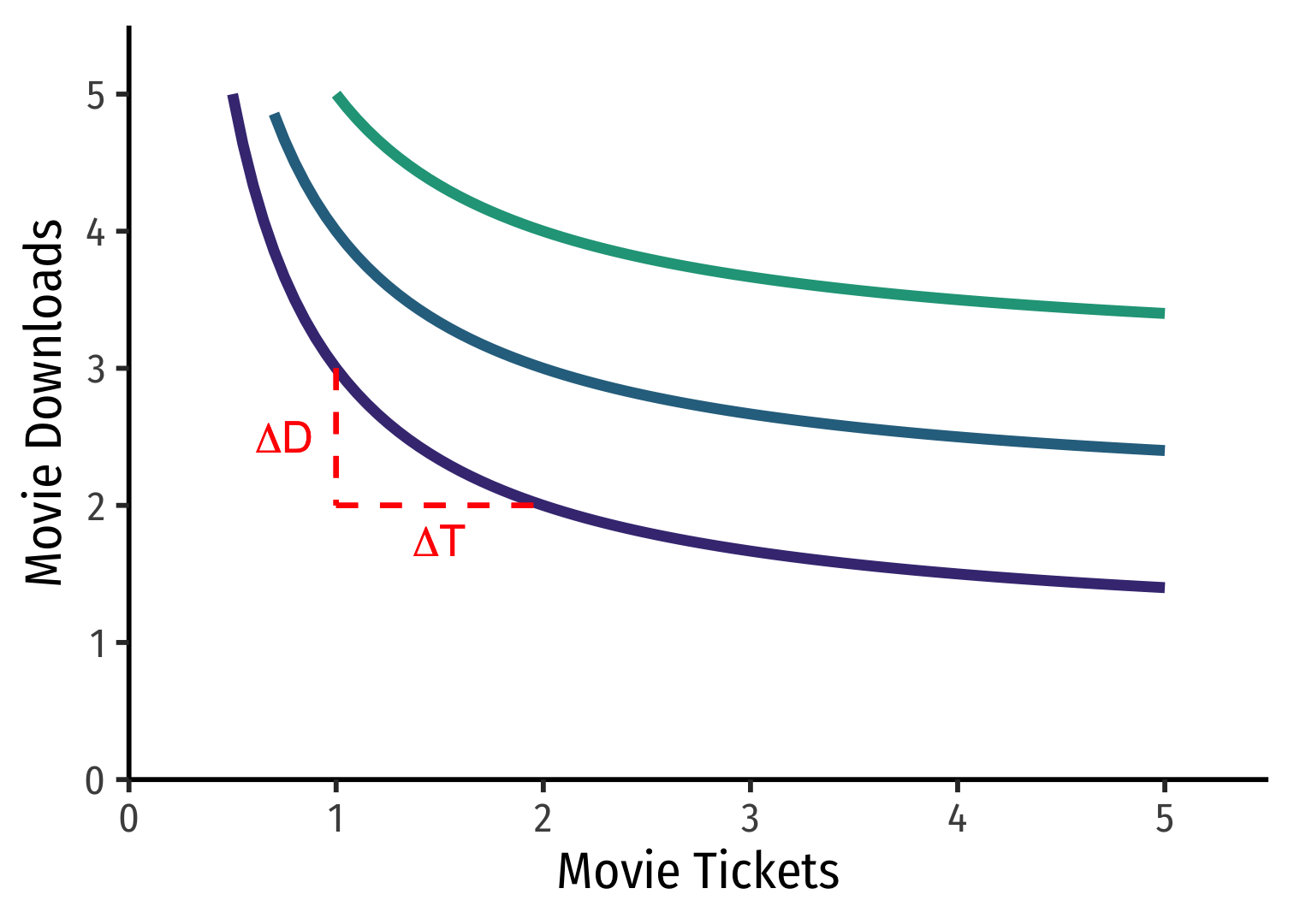
- Flatter → willing to give up few Downloads per Ticket (and vice versa)
- MRST,D is small
MRS and Preferences: Steepness II

- Flatter → willing to give up few Downloads per Ticket (and vice versa)
- MRST,D is small
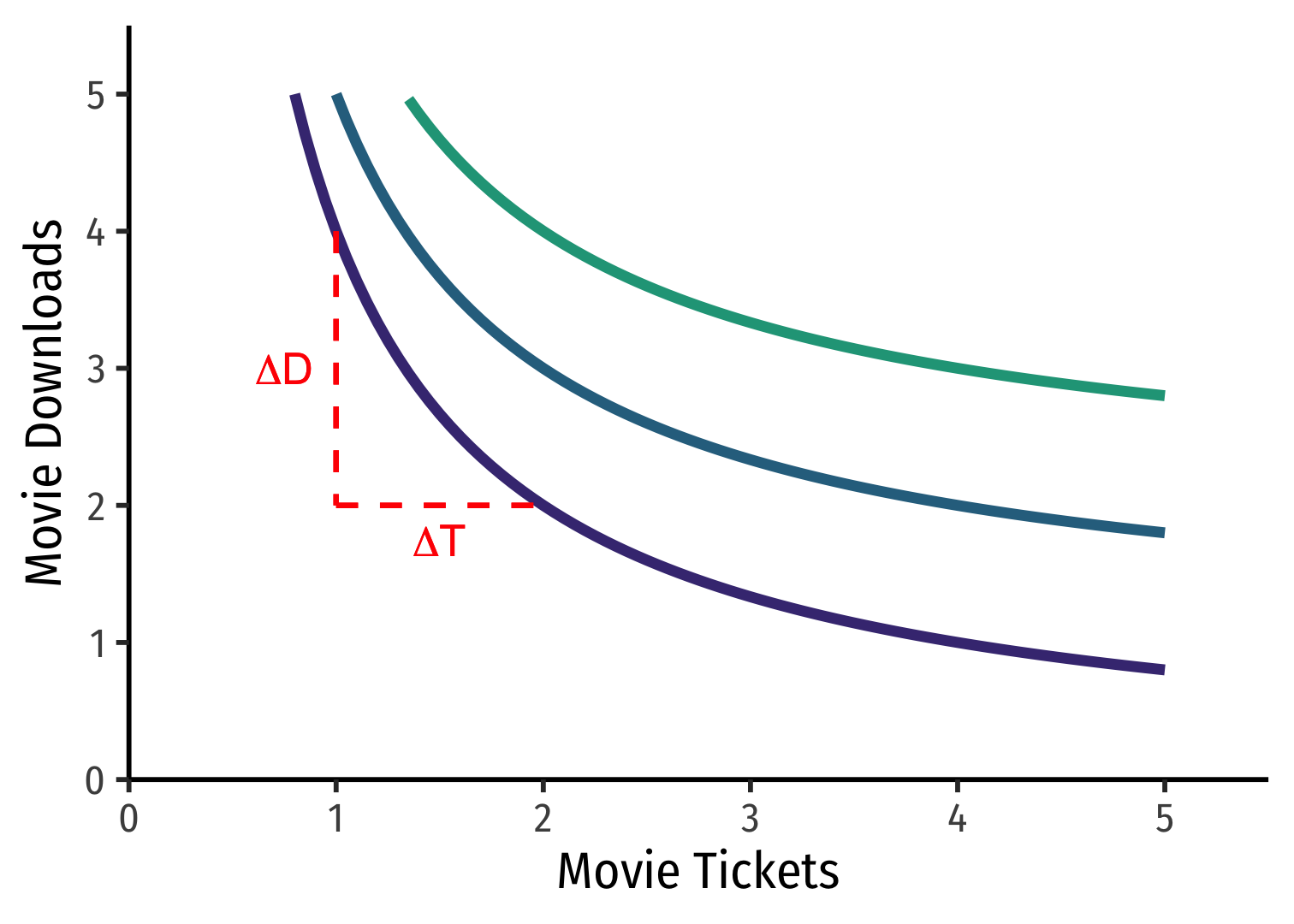
- Steeper → willing to give up more Downloads per Ticket (and vice versa)
- MRST,D is large
MRS and Preferences: Goods, Bads, Neutrals
Now we have better ways to classify objects:
A good enters utility function positively
- ↑ good ⟹ ↑ utility (and vice versa)
- Willing to pay (give up other goods) to acquire more (monotonic)

MRS and Preferences: Goods, Bads, Neutrals
Now we have better ways to classify objects:
A good enters utility function positively
- ↑ good ⟹ ↑ utility (and vice versa)
- Willing to pay (give up other goods) to acquire more (monotonic)
A bad enters utility function negatively
- ↑ good ⟹ ↓ utility (and vice versa)
- Willing to pay (give up other goods) to get rid of

MRS and Preferences: Goods, Bads, Neutrals
Now we have better ways to classify objects:
A good enters utility function positively
- ↑ good ⟹ ↑ utility (and vice versa)
- Willing to pay (give up other goods) to acquire more (monotonic)
A bad enters utility function negatively
- ↑ good ⟹ ↓ utility (and vice versa)
- Willing to pay (give up other goods) to get rid of
A neutral does not enter utility function at all
- ↑,↓ has no effect on utility

MRS and Preferences: Curvature
MRS=ΔyΔx⏟slope=−MUxMUy
Curvature of indifference curves tells us how goods are related
Relatively straight curves: goods are more substitutable for one another
Relatively bent curves: goods are more complementary with one another
Look at extreme cases first to get the idea
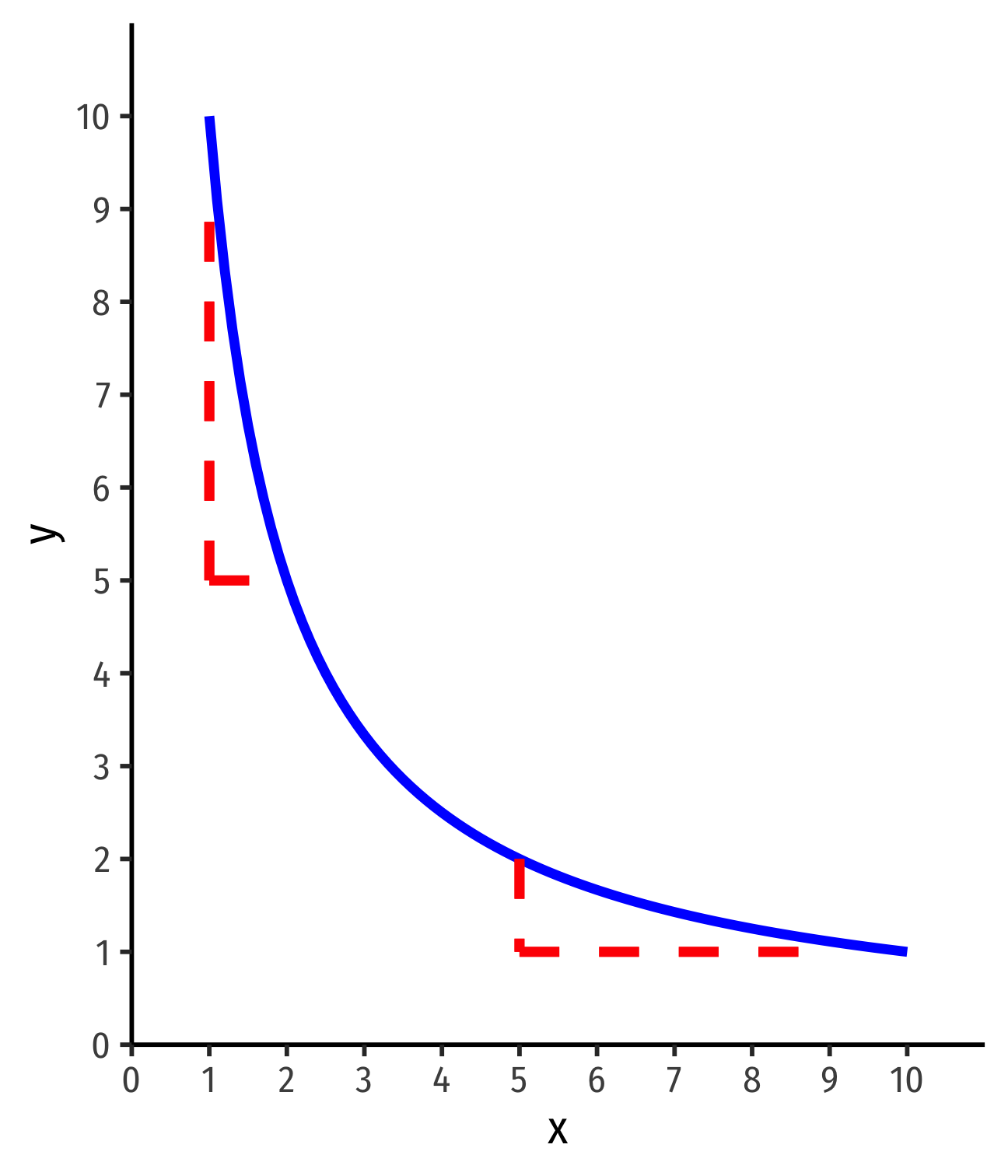
MRS and Preferences: Curvature II
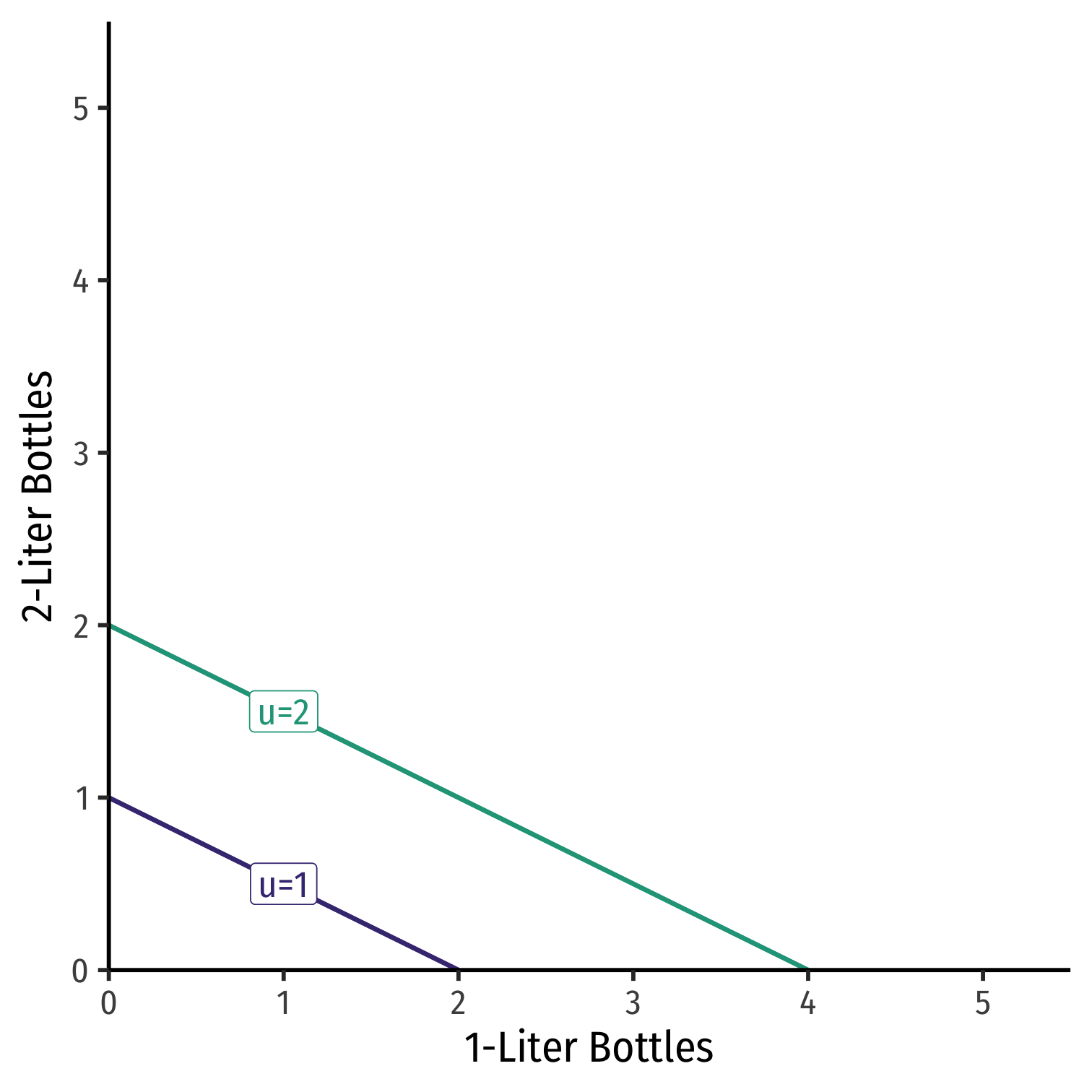
Example: Consider 1-Liter bottles of coke and 2-Liter bottles of coke
Always willing to substitute Two 1-Ls:One 2-L
Perfect substitutes: goods that can be substituted at same fixed rate and yield same utility
(MRS_{1L,2L}=-0.5)(a constant!)
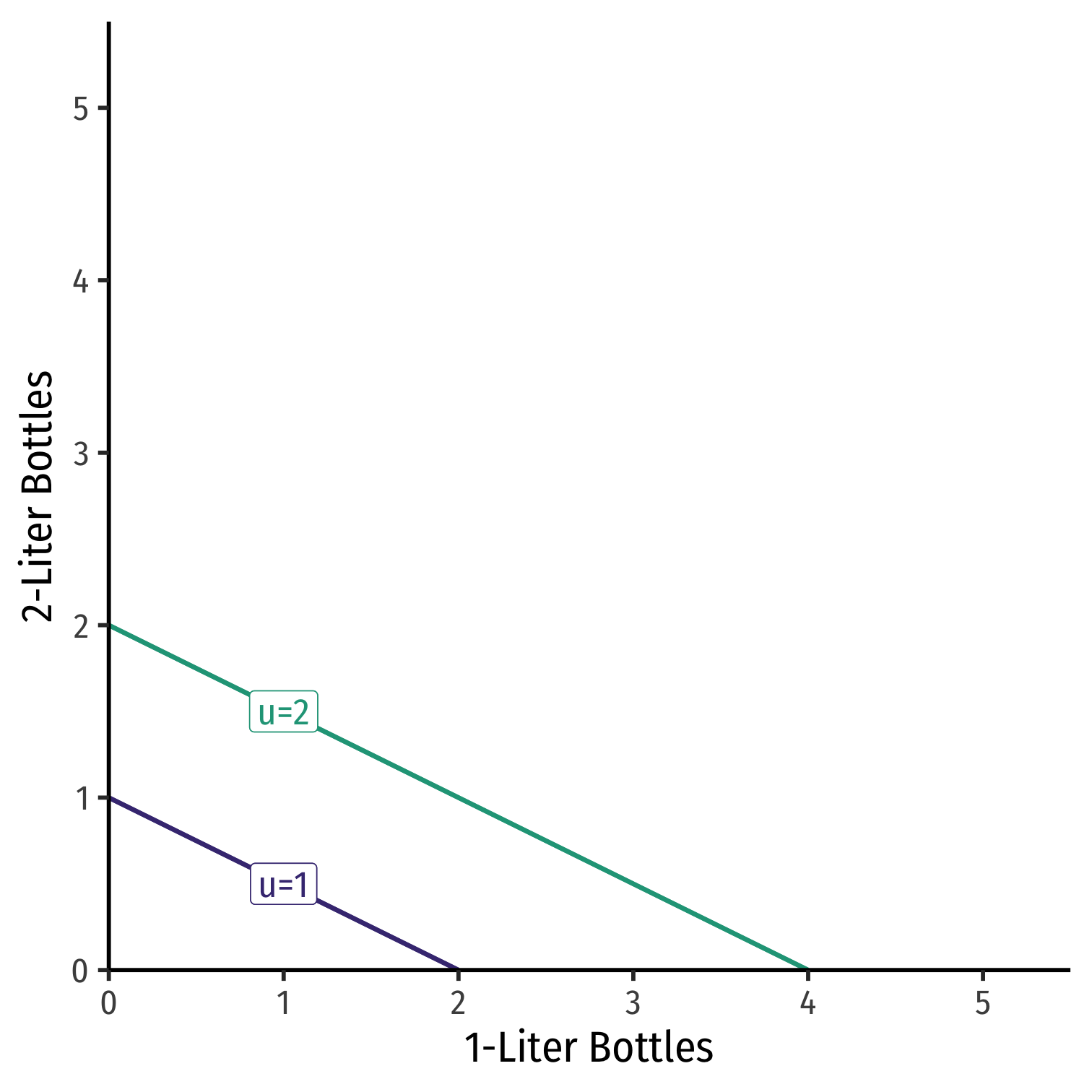
MRS and Preferences: Curvature III
Math FYI: Utility functions for substitutes
u(x,y)=wxx+wyy
wi: relative weight (intensity of relative preference)
Known as linear preferences
Example uL1,L2=1L1+2L2
- MRSL1,L2=−wxwy=−12
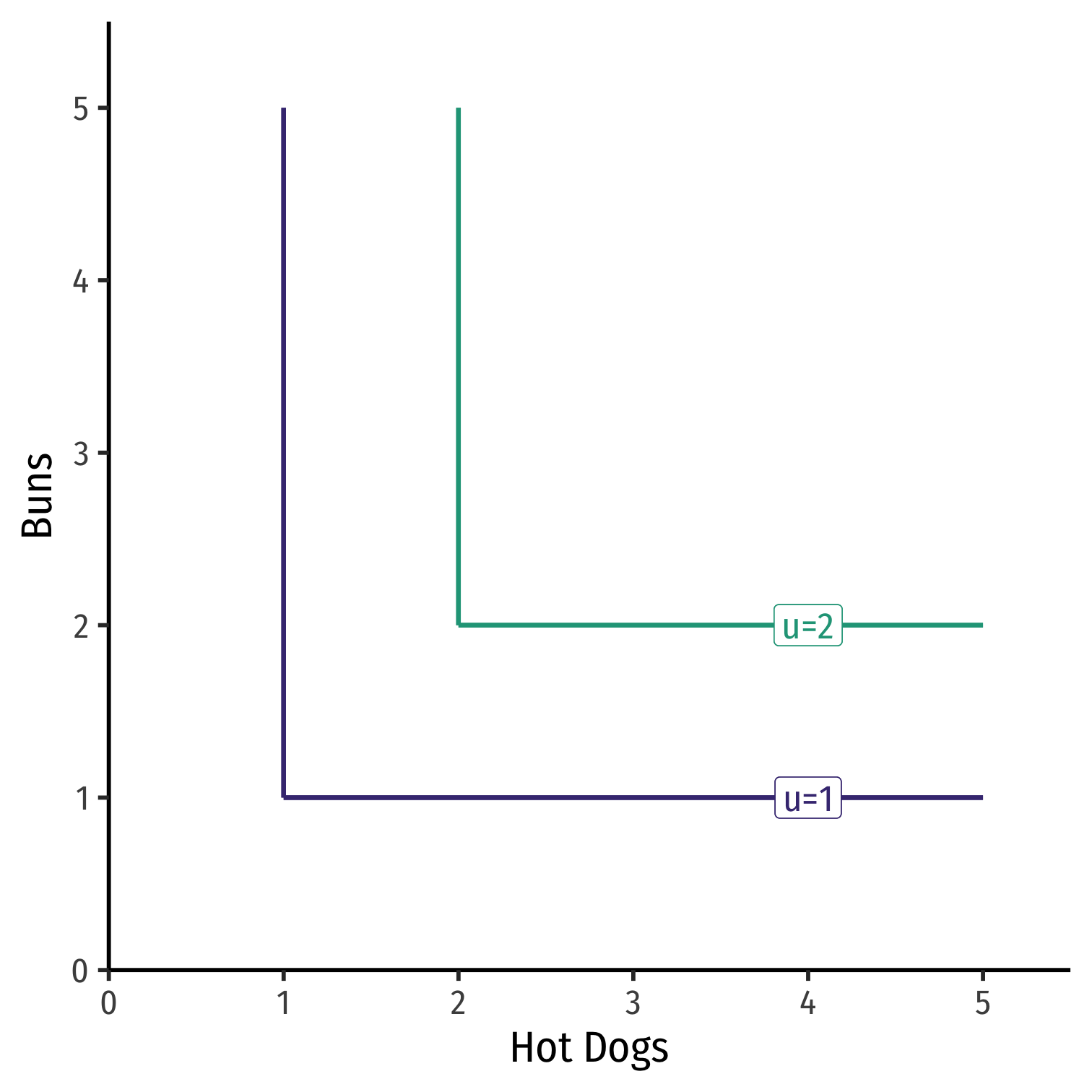
MRS and Preferences: Curvature IV
Example: Consider hot dogs and hot dog buns
Always consume together in fixed proportions (1:1)
Perfect complements: goods that can be consumed together in same fixed proportion and yield same utility
MRS: ?
MRS and Preferences: Curvature V
Math FYI: Utility functions for complements
u(x,y)=min{wxx,wyy}
wi: relative weight (intensity of relative preference)
MRS =0,∞, or undefined
Known as Leontief preferences
Example u(H,B)=min{H,B}
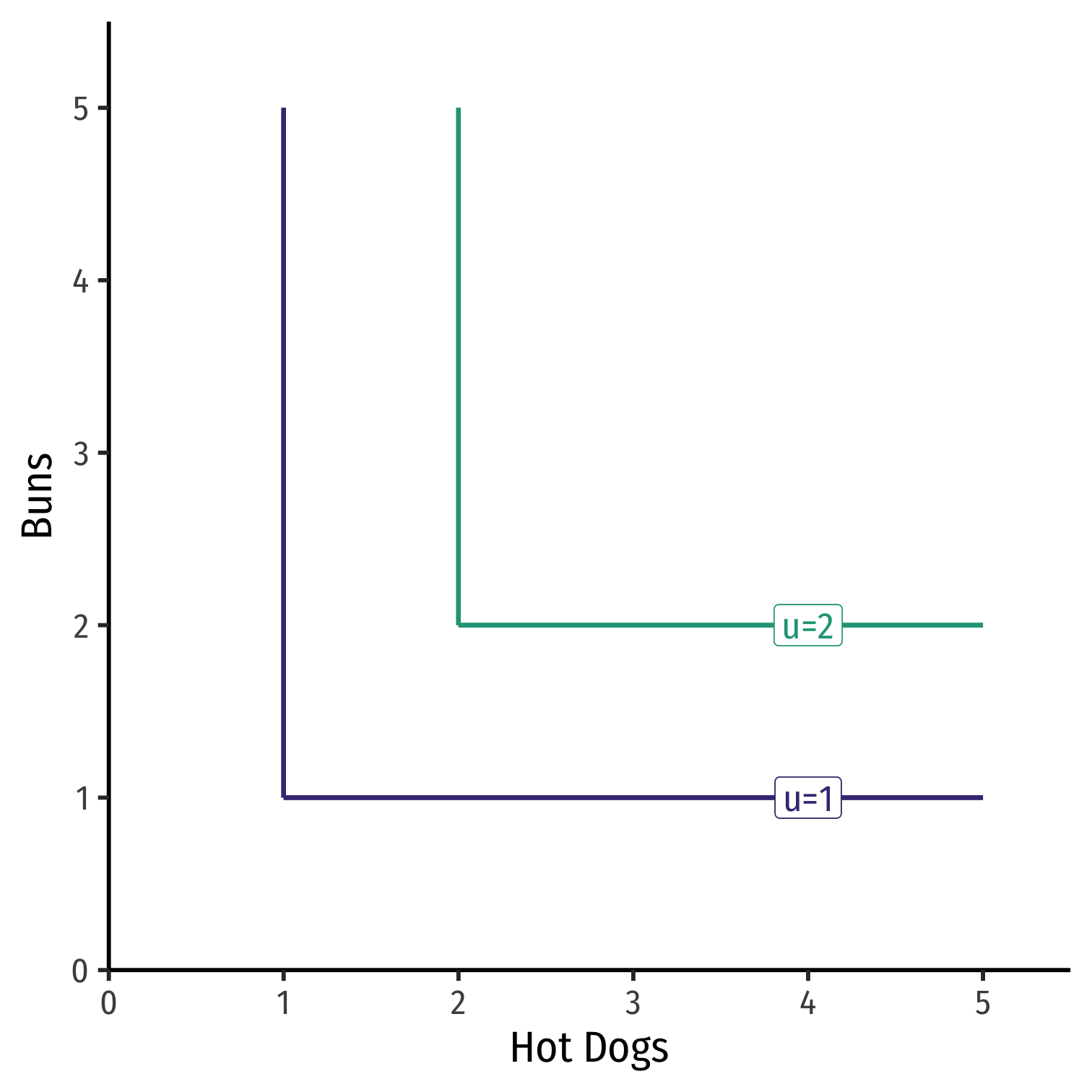
MRS and Preferences: Curvature VI
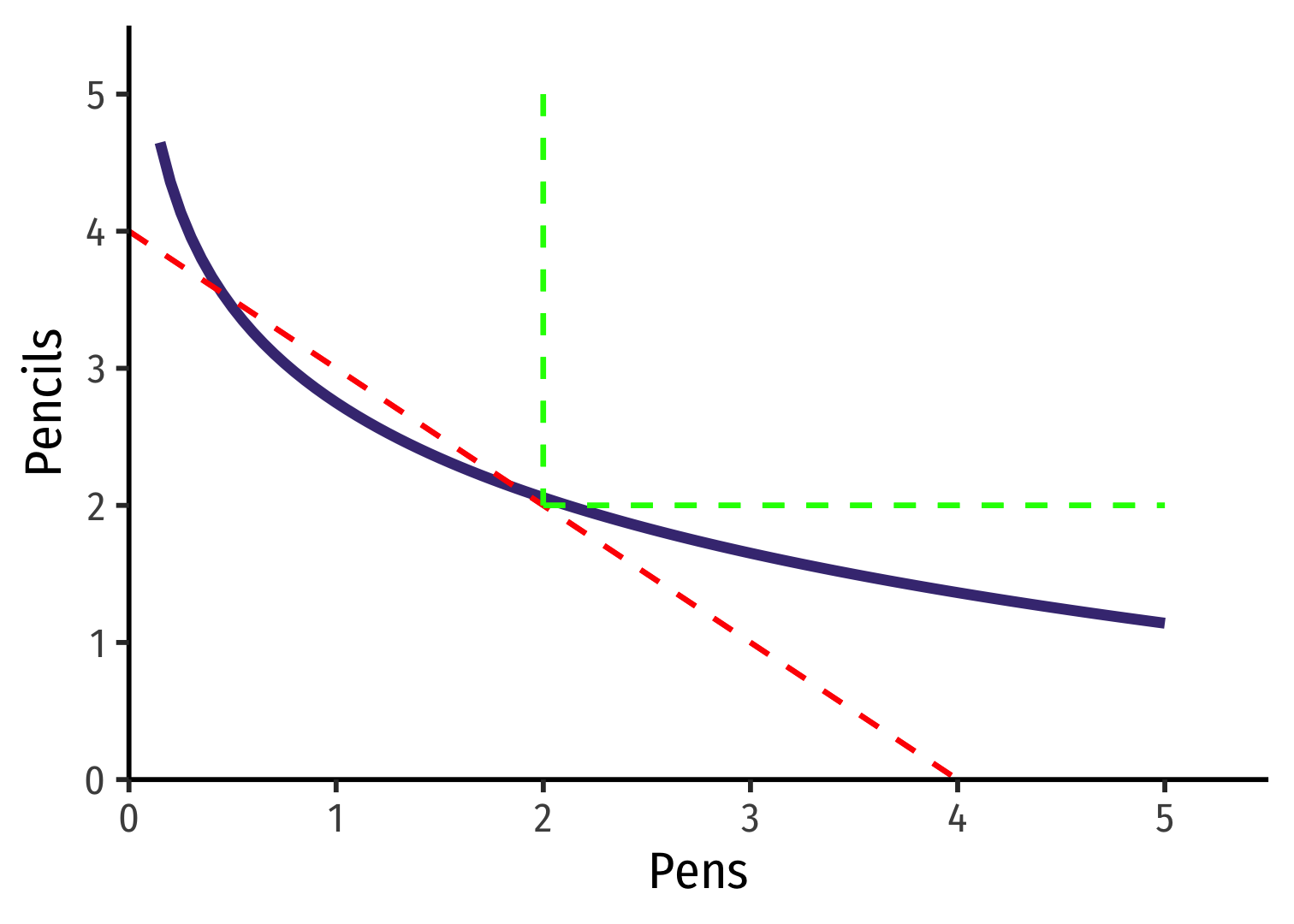
- Straighter → more substitutable
MRS and Preferences: Curvature VI

- Straighter → more substitutable
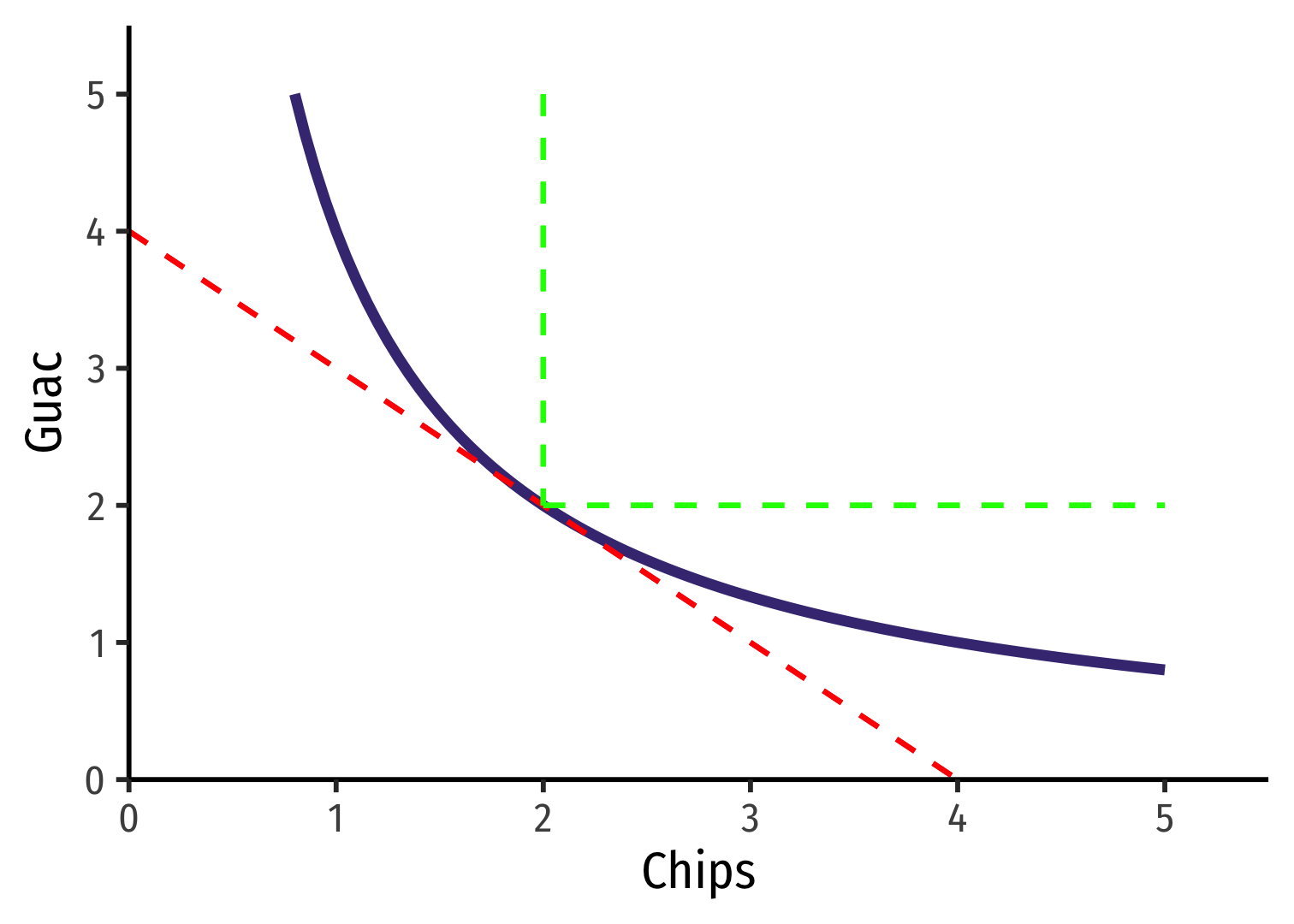
- Curved → more complementary
Cobb-Douglas Utility Functions
- A very common functional form in economics is Cobb-Douglas
u(x,y)=xayb
- Where a,b>0 (and very often a+b=1)
- Extremely useful, you will see it often!
- Strictly convex and monotonic indifference curves
- Other nice properties (we'll see later)
- See the appendix in today's class page
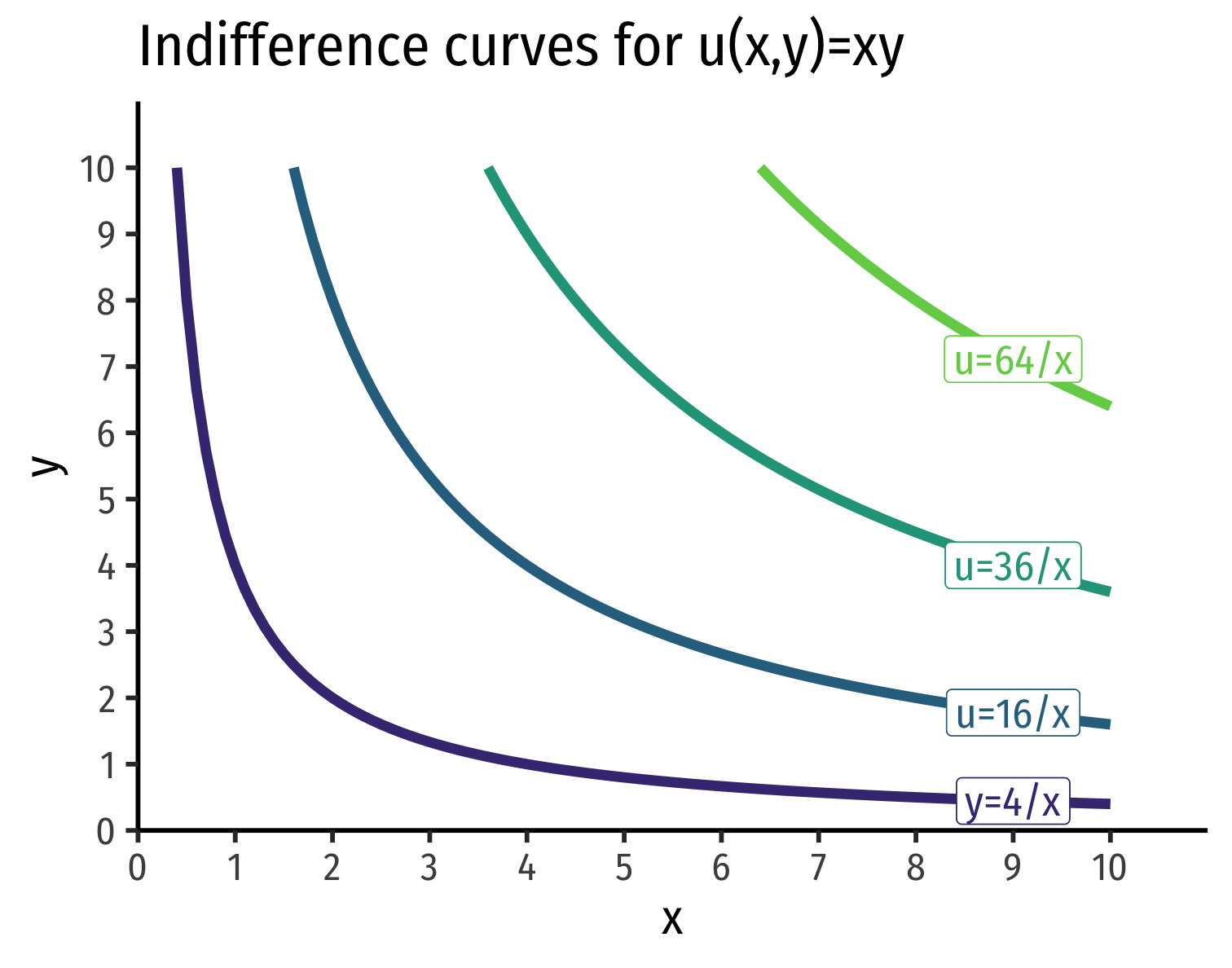
Practice
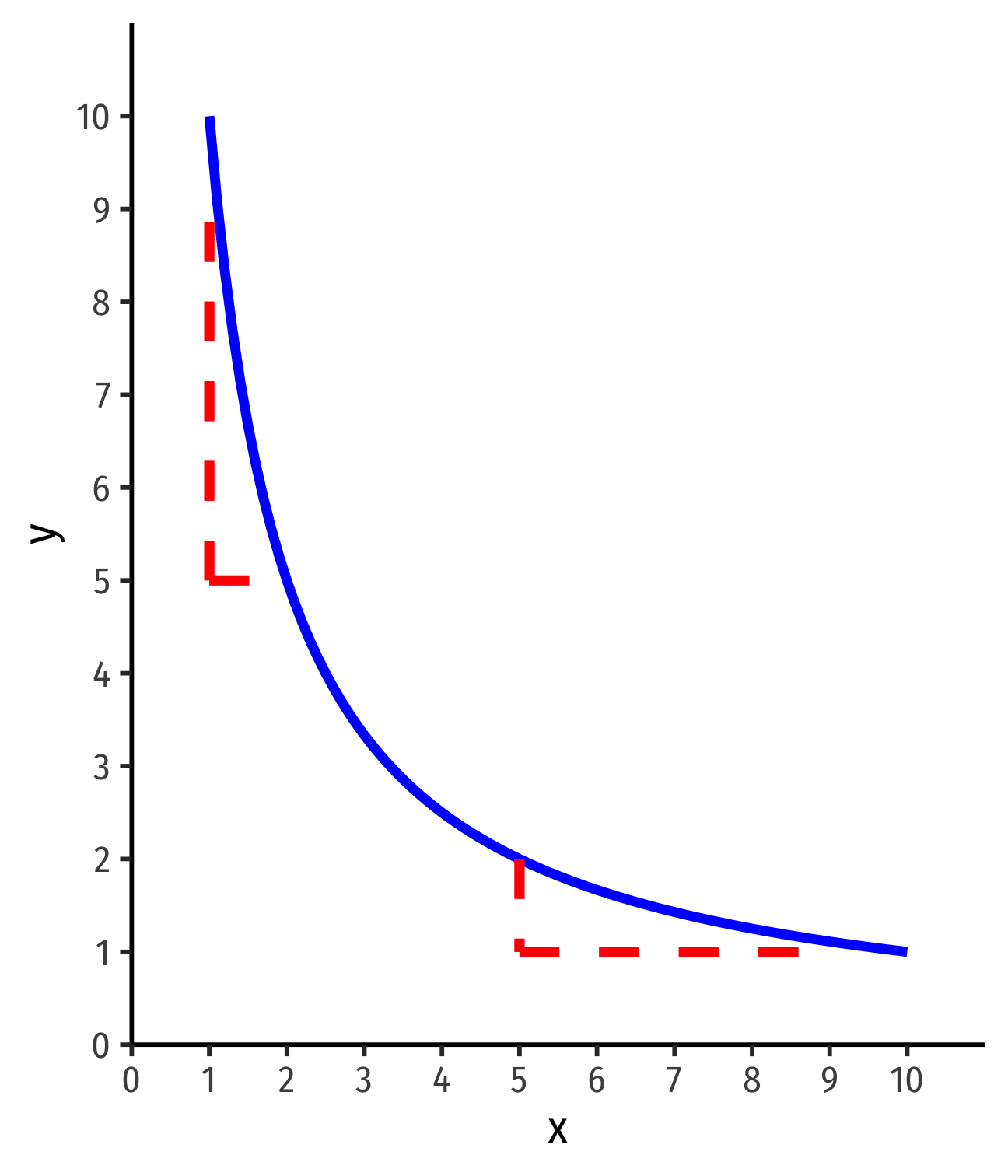
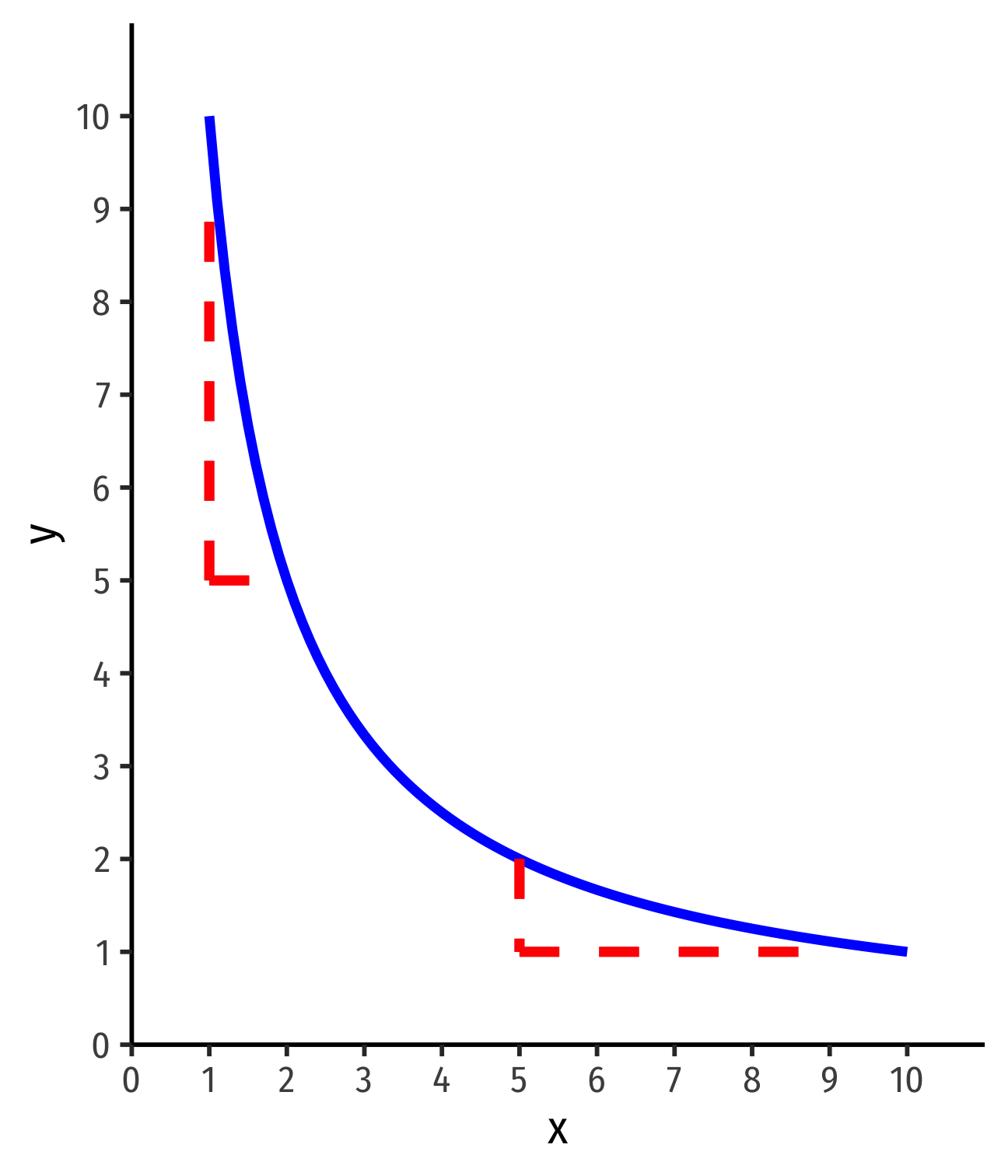
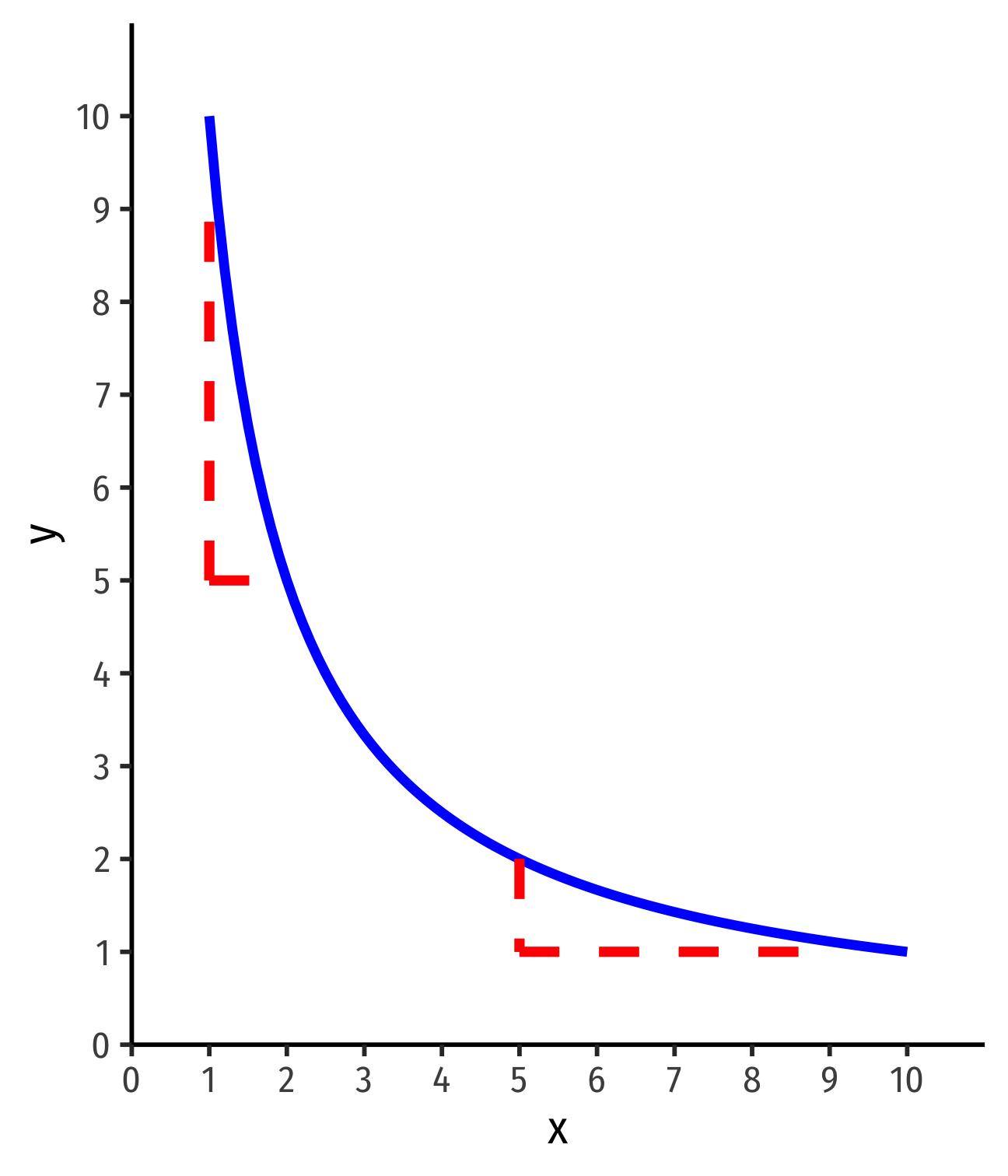
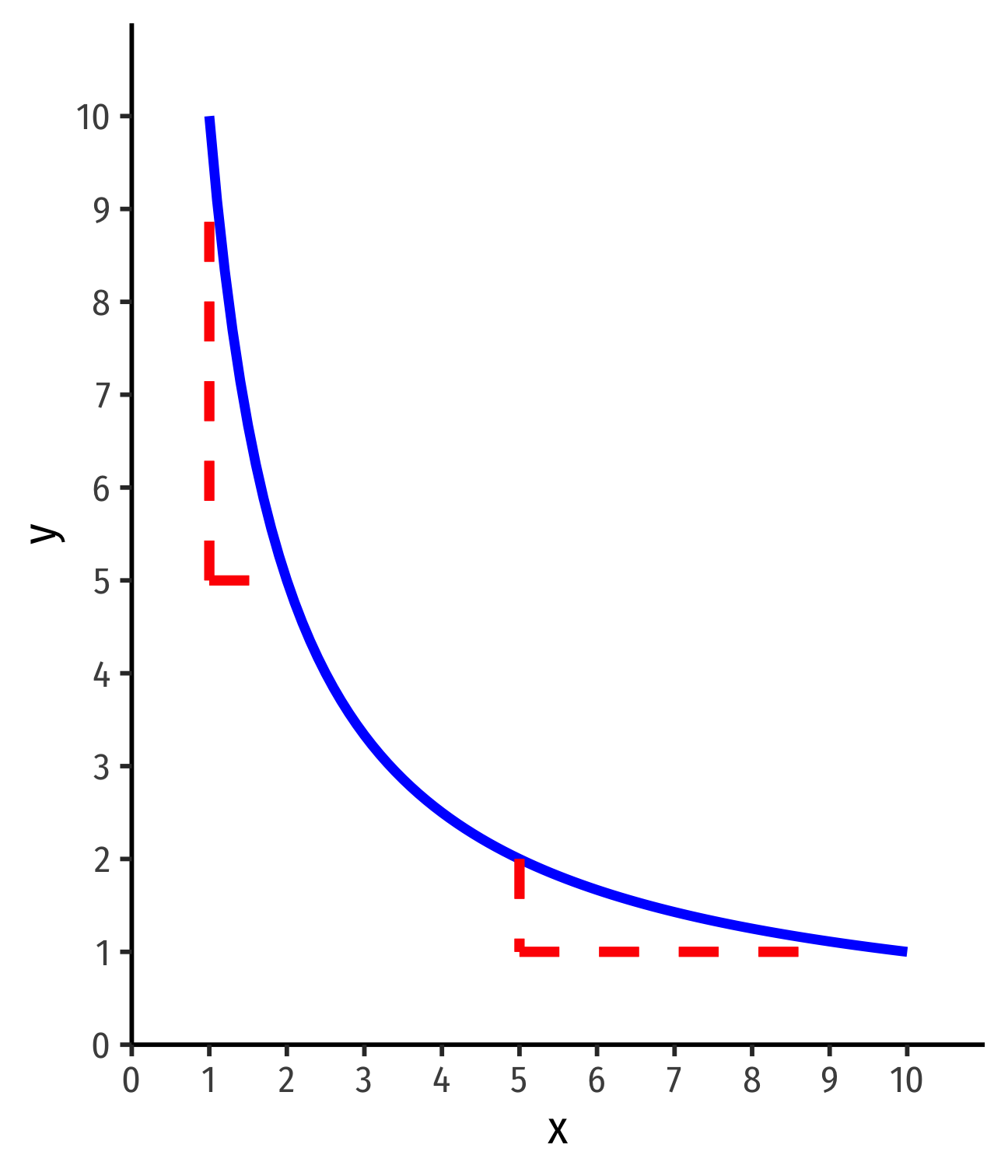
Example: Suppose you can consume apples (a) and broccoli (b), and earn utility according to the utility function: u(a,b)=2ab
Where your marginal utilities are:
MUa=2bMUb=2a
Put a on the horizontal axis and b on the vertical axis. Write an equation for MRSa,b.
Would bundles of (1,4) and (2,2) be on the same indifference curve?
Sketch a graph of the indifference curve from part 2. (Bonus: find the equation of this indifference curve. See the appendix in today's class page.)
Is this curve convex? Hint: Does MRSa,b↓ as a↑?