Consumer's Objectives
What do consumers want? What do they maximize?
Avoid being normative & make as few assumptions as possible
We'll assume people maximize preferences
- WTF does that mean?
Preferences I
- Which bundles of (x,y) are preferred over others?
Example:
Bundle a=(412) or Bundle b=(612)
Preferences II
- We will allow three possible answers:
Preferences II
- We will allow three possible answers:
- a≻b: Strictly prefer a over b
Preferences II
- We will allow three possible answers:
a≻b: Strictly prefer a over b
a≺b: Strictly prefer b over a
Preferences II
- We will allow three possible answers:1
a≻b: Strictly prefer a over b
a≺b: Strictly prefer b over a
a∼b: Indifferent between a and b
- Preferences are a list of all such comparisons between all bundles
1 Note you can allow for "weak" preferences: (a⪰b), i.e. "a is at least as good as b." We use "strict" preferences to keep it simple.
Assumptions About Preferences
- We assume preferences are "well-behaved" to model:
Assumptions About Preferences
- We assume preferences are "well-behaved" to model:
- Reflexivity : any bundle is at least as preferred as itself:
a⪰a
Assumptions About Preferences
- We assume preferences are "well-behaved" to model:
Reflexivity : any bundle is at least as preferred as itself: a⪰a
Completeness : any two bundles can be ranked: a⪰b or a⪯b or a∼b∀(a,b)∈R+
Assumptions About Preferences
- We assume preferences are "well-behaved" to model:
Reflexivity : any bundle is at least as preferred as itself: a⪰a
Completeness : any two bundles can be ranked: a⪰b or a⪯b or a∼b∀(a,b)∈R+
Transitivity : rankings are logically consistent:
- If a≻b and b≻c, then a≻c
- Are these good assumptions? As usual in economics: very very often yes, sometimes no!
Mapping Preferences Graphically I
For each bundle, we now have 3 pieces of information:
- amount of x
- amount of y
- preference compared to other bundles
How to represent this information graphically?
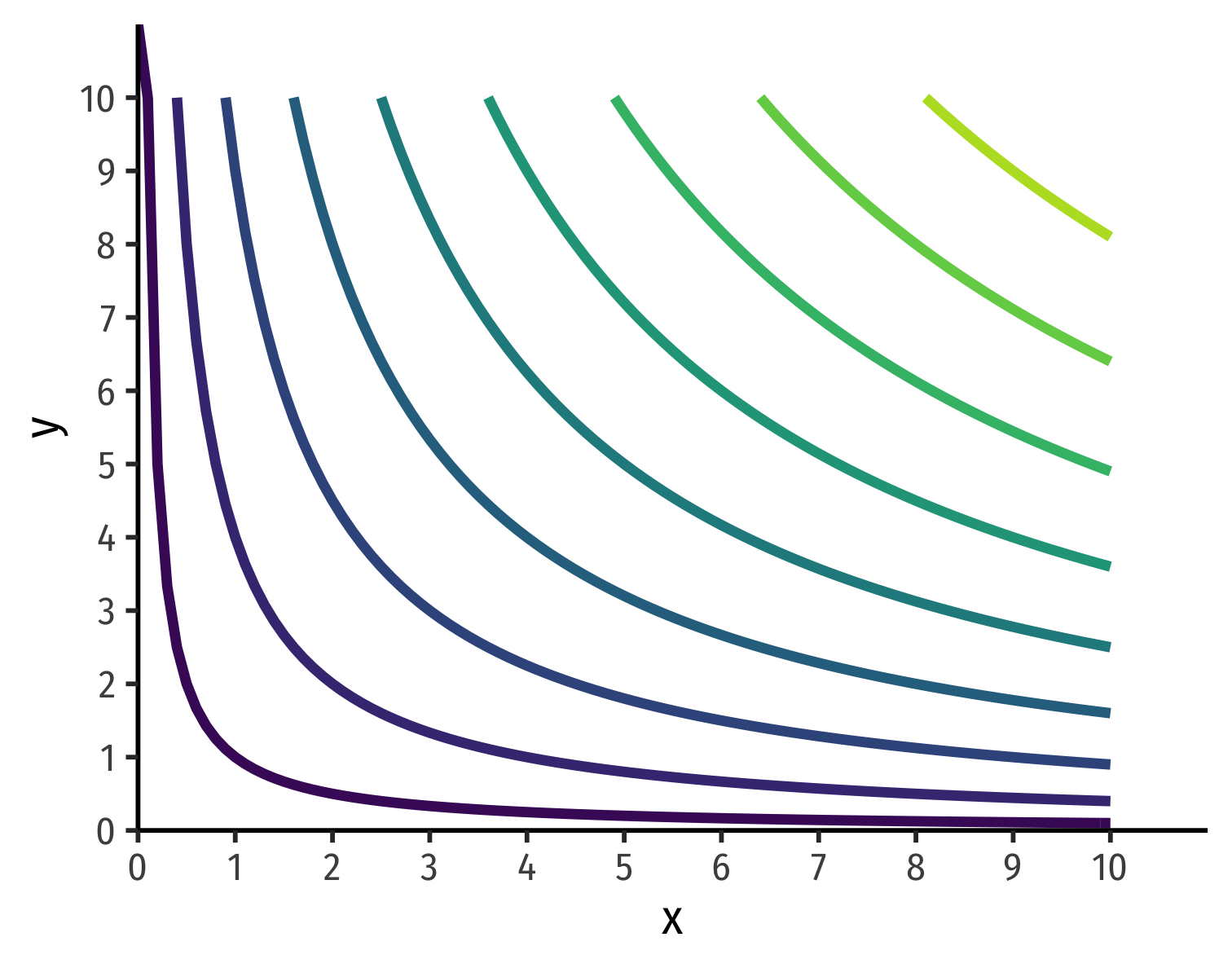
Mapping Preferences Graphically II
Cartographers have the answer for us
On a map, contour lines link areas of equal height
We will use "indifference curves" to link bundles of equal preference
Mapping Preferences Graphically III
3-D "Mount Utility"
2-D Indifference Curve Contours
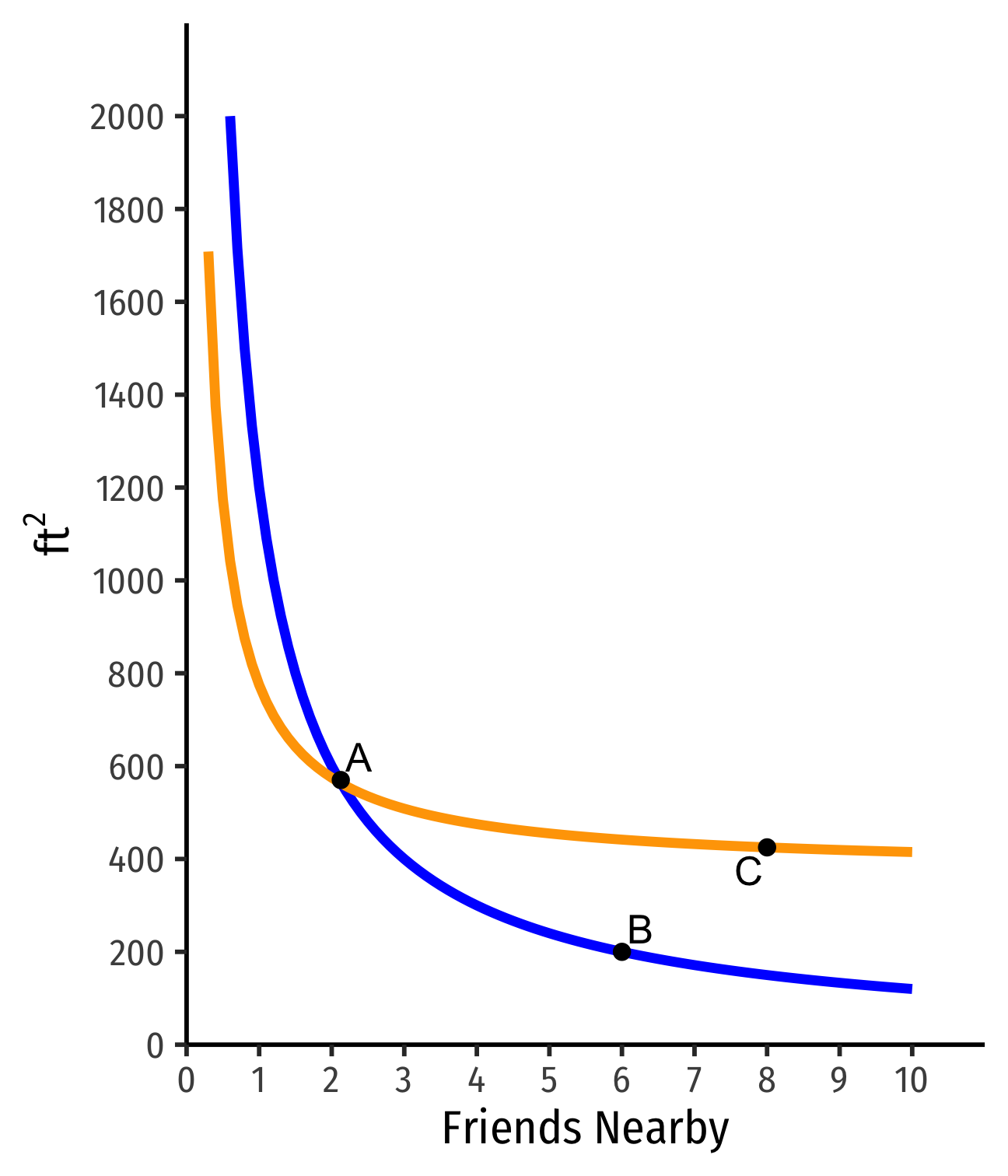
Indifference Curves: Example
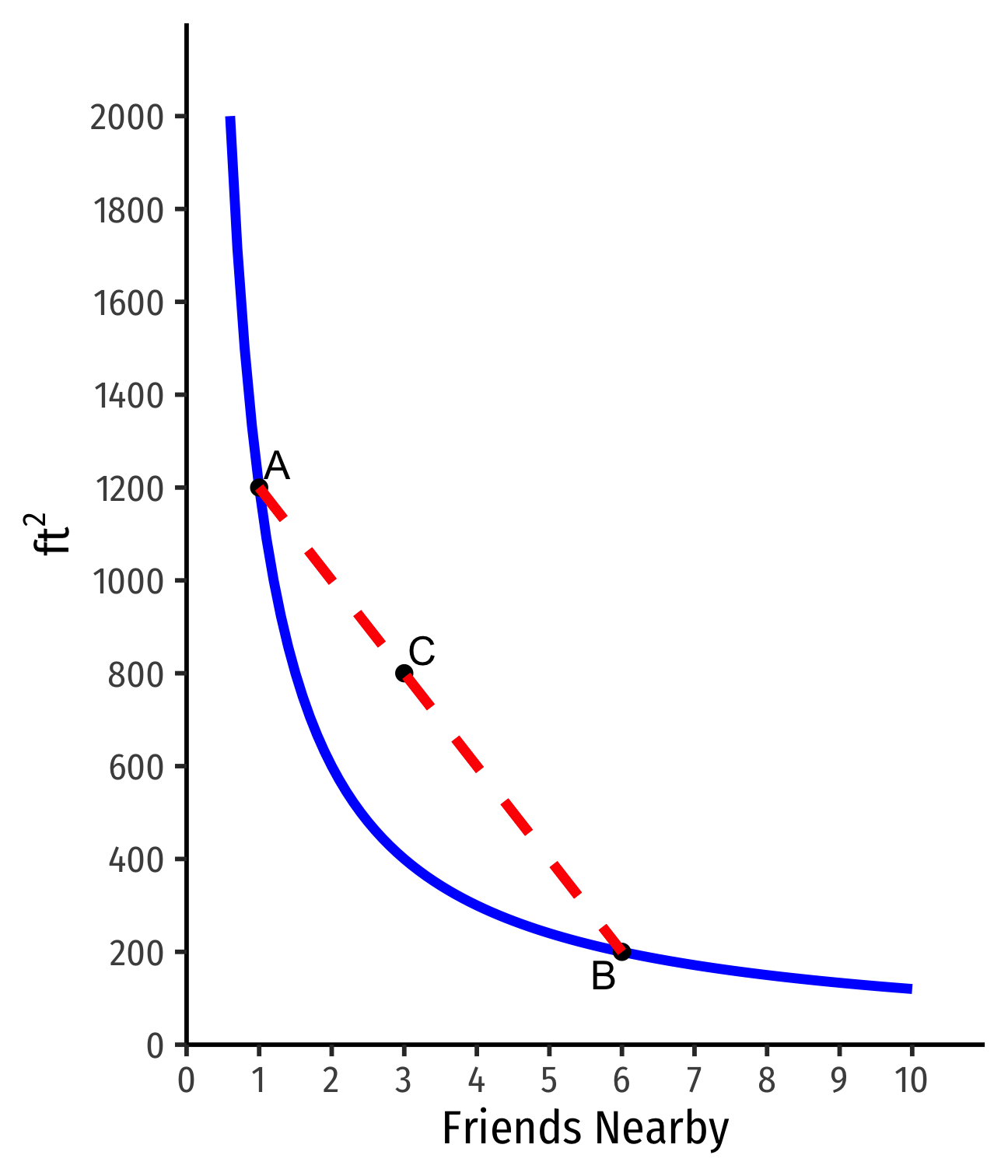
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
Indifference Curves: Example
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
- Apartment A has 1 friend nearby and is 1,200 ft2
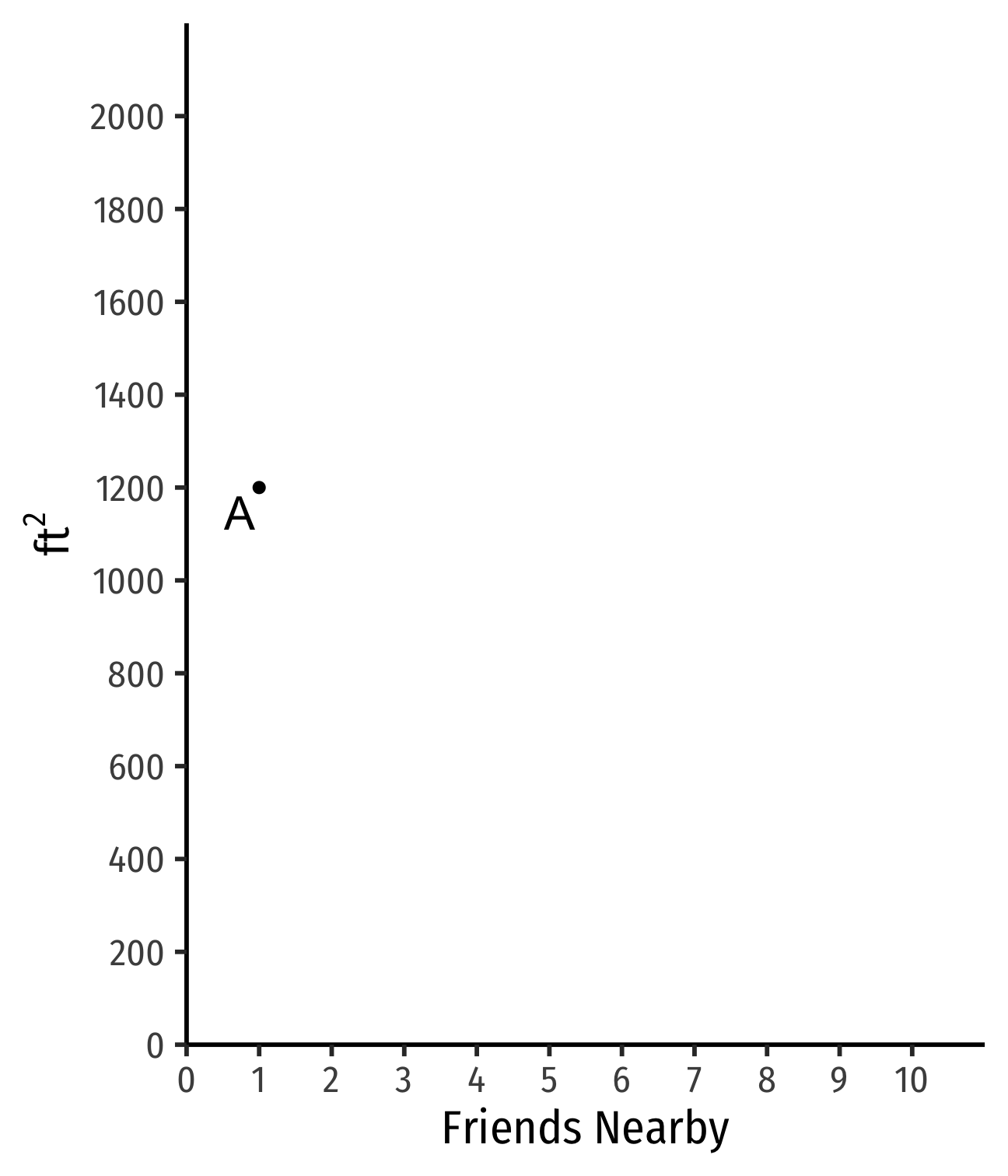
Indifference Curves: Example
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
- Apartment A has 1 friend nearby and is 1,200 ft2
- Apartments that are larger and/or have more friends ≻A
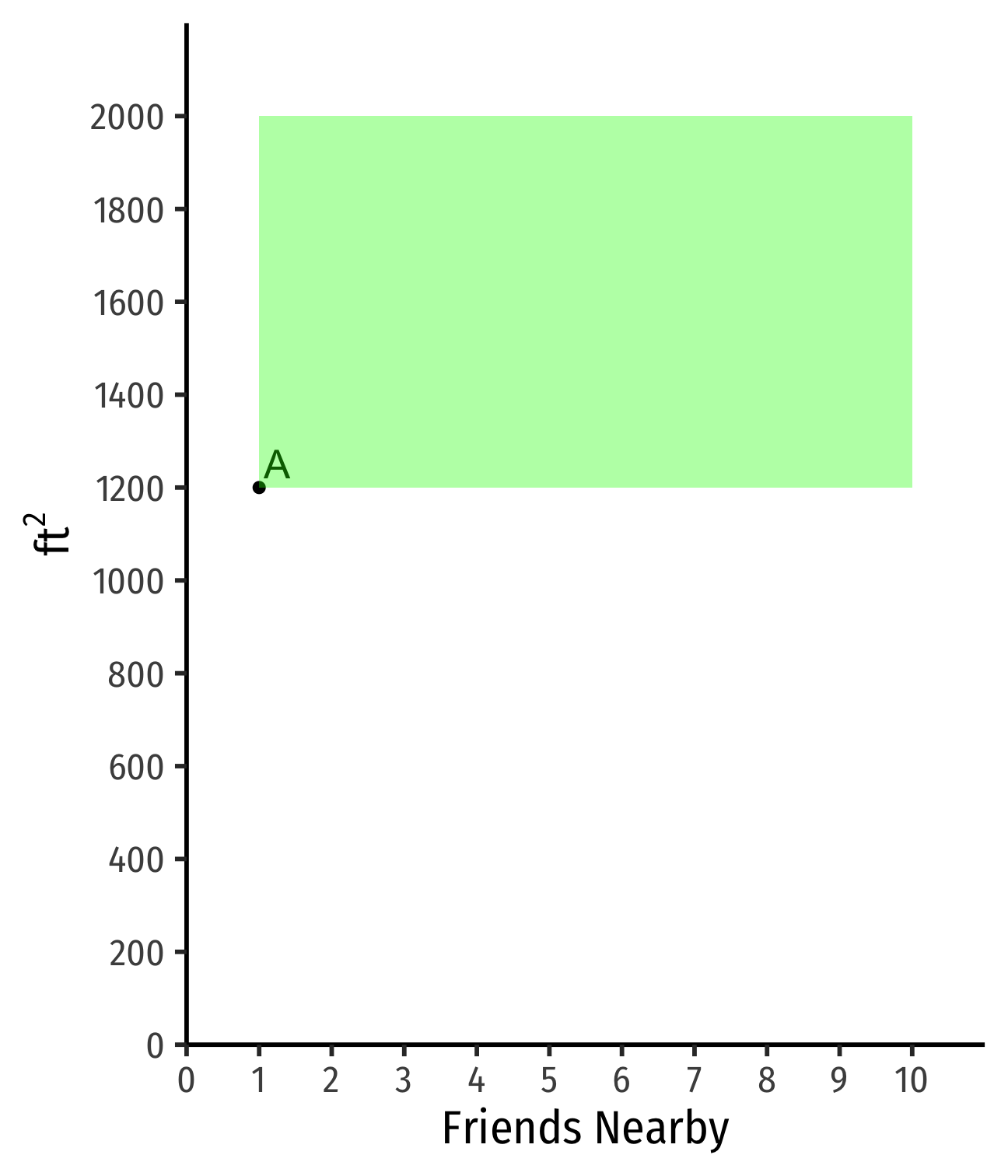
Indifference Curves: Example
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
- Apartment A has 1 friend nearby and is 1,200 ft2
- Apartments that are larger and/or have more friends ≻A
- Apartments that are smaller and/or have fewer friends ≺A
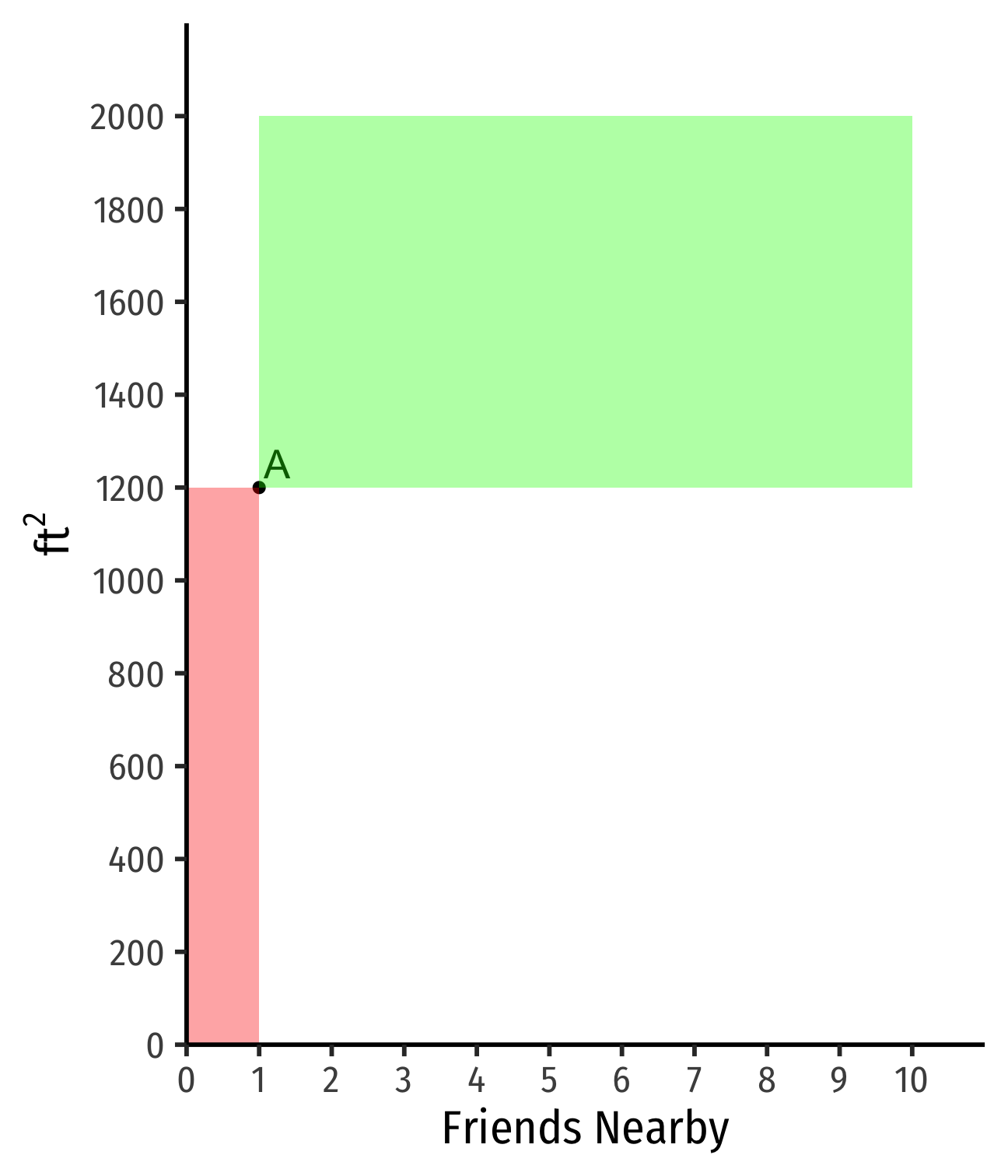
Indifference Curves: Example
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
Apartment A has 1 friend nearby and is 1,200 ft2
Apartment B has more friends but less ft2
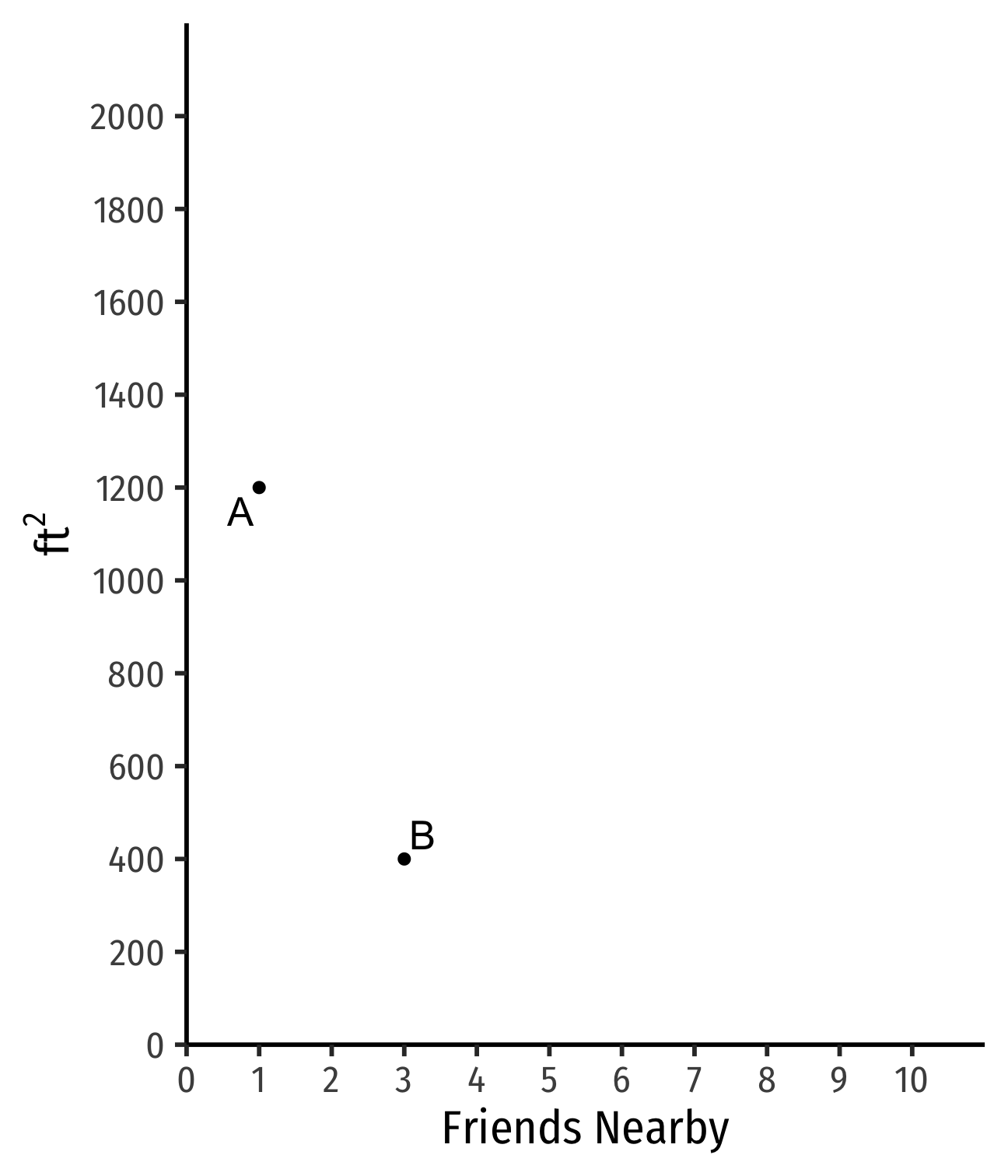
Indifference Curves: Example
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
Apartment A has 1 friend nearby and is 1,200 ft2
Apartment B has more friends but less ft2
Apartment C has still more friends but less ft2
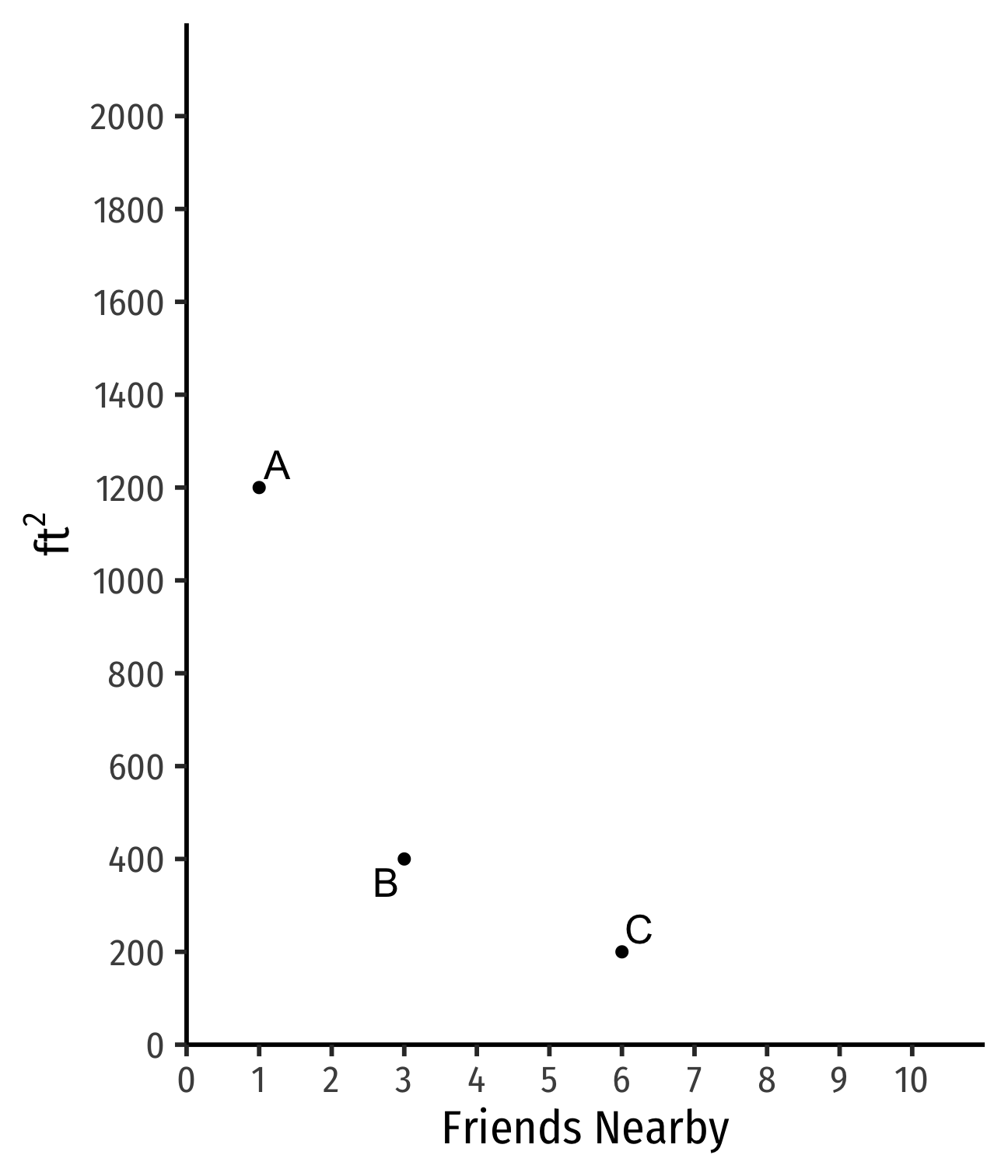
Indifference Curves: Example
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
Apartment A has 1 friend nearby and is 1,200 ft2
Apartment B has more friends but less ft2
Apartment C has still more friends but less ft2
If A∼B∼C, these apartments are on the same indifference curve
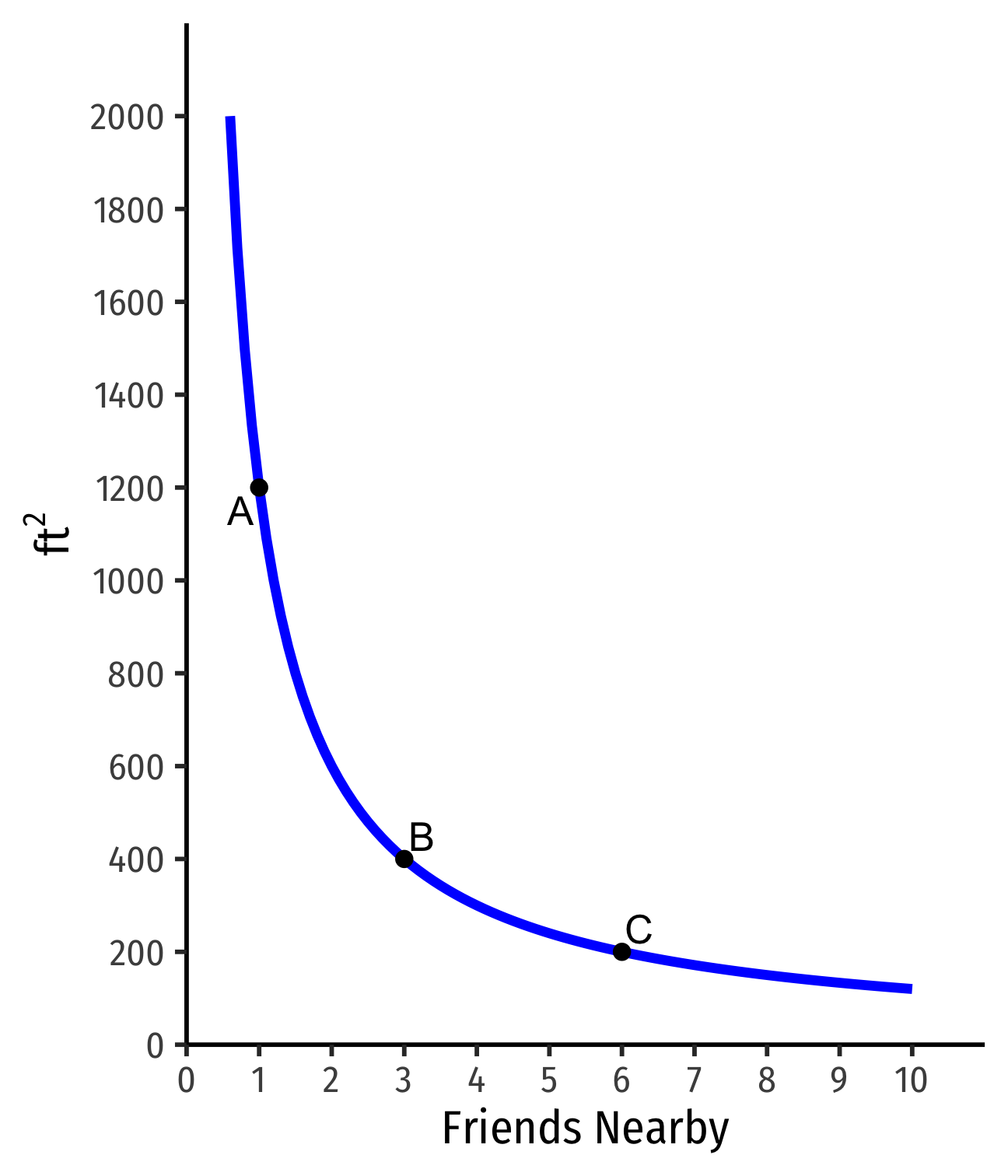
Indifference Curves: Example
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
- Indifferent between all apartments on the same curve
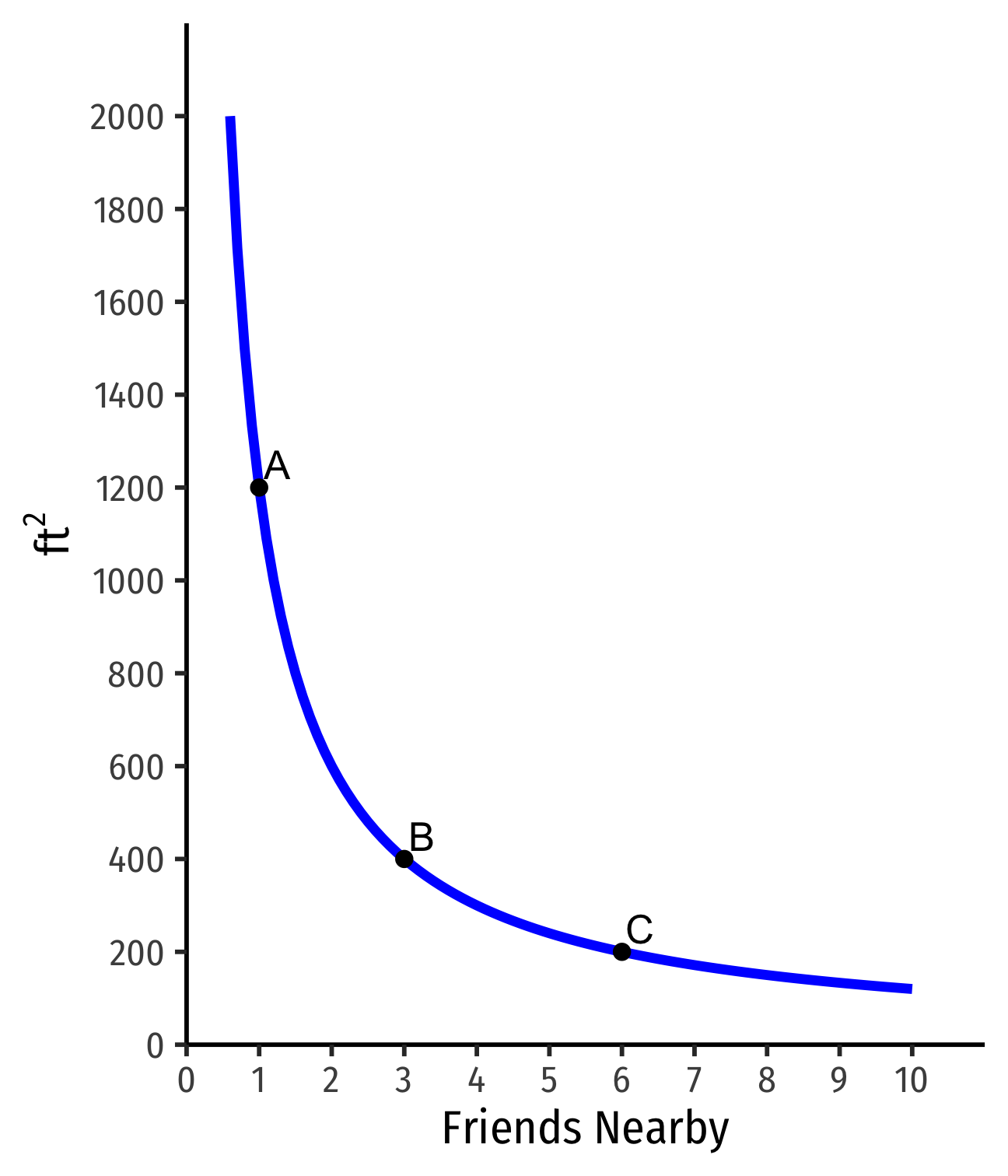
Indifference Curves: Example
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
Indifferent between all apts on the same curve
Apts above the curve are preferred over apts on the curve
- D≻A∼B∼C
- On a higher curve
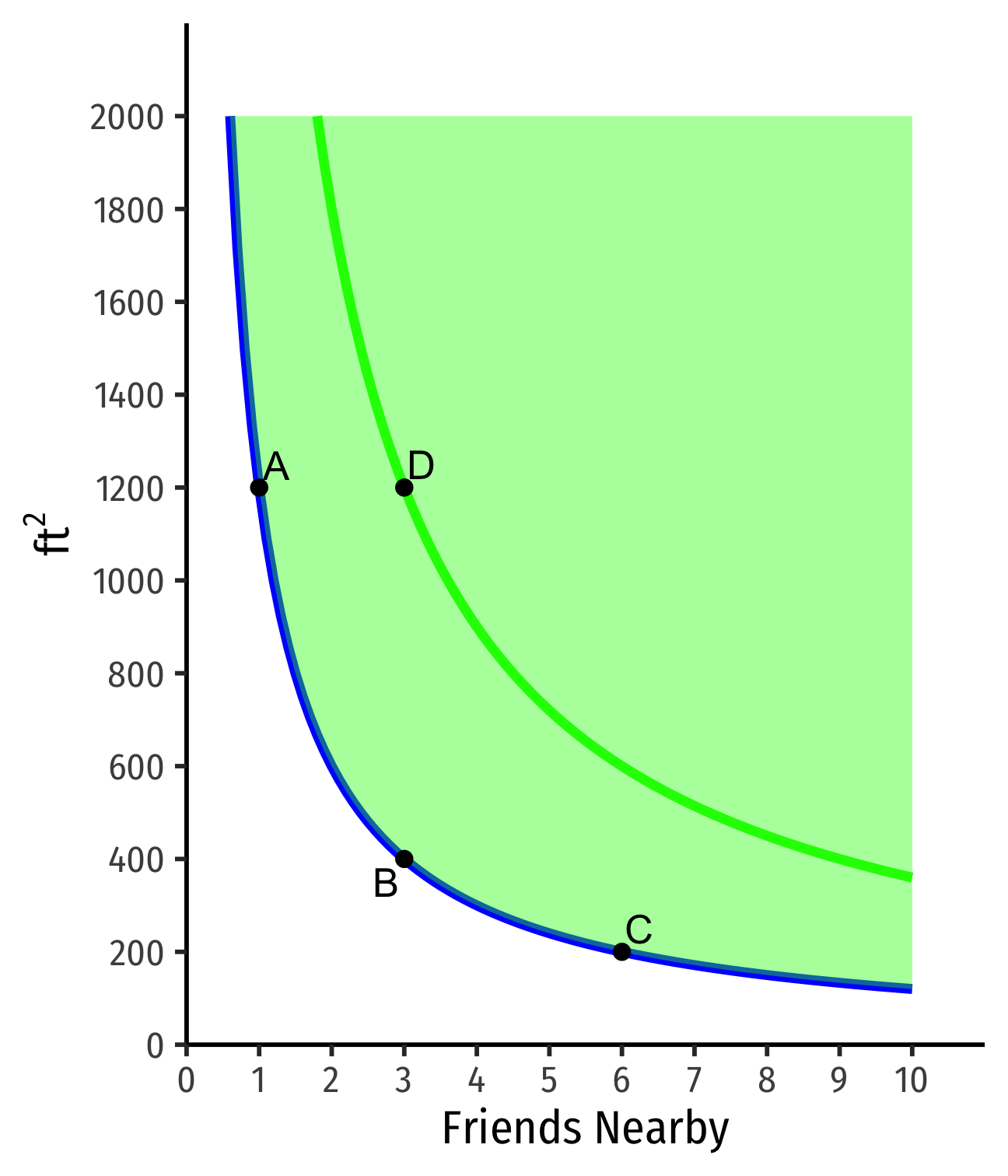
Indifference Curves: Example
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
Indifferent between all apts on the same curve
Apts above curve are preferred over apts on curve
- D≻A∼B∼C
- Actually on a higher curve
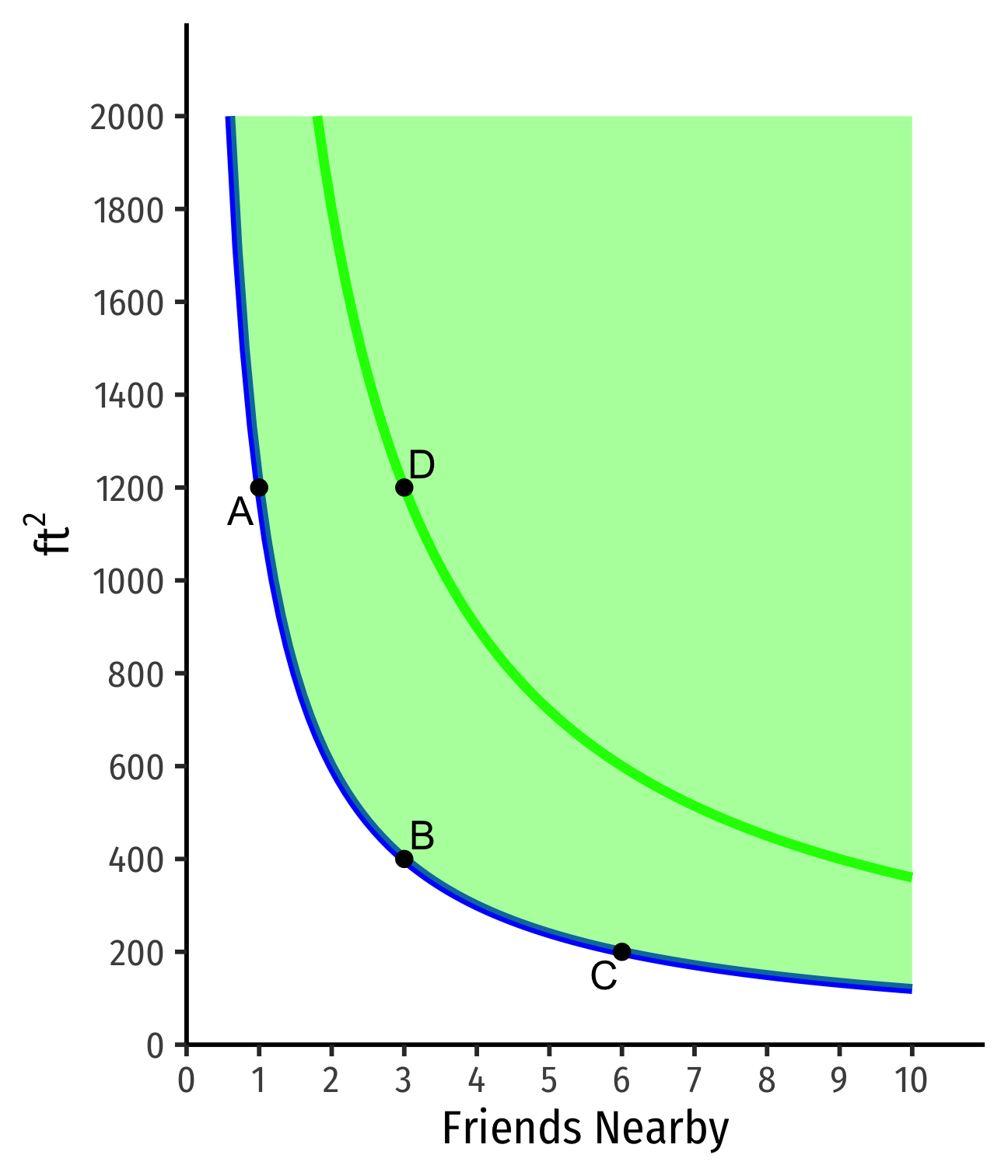
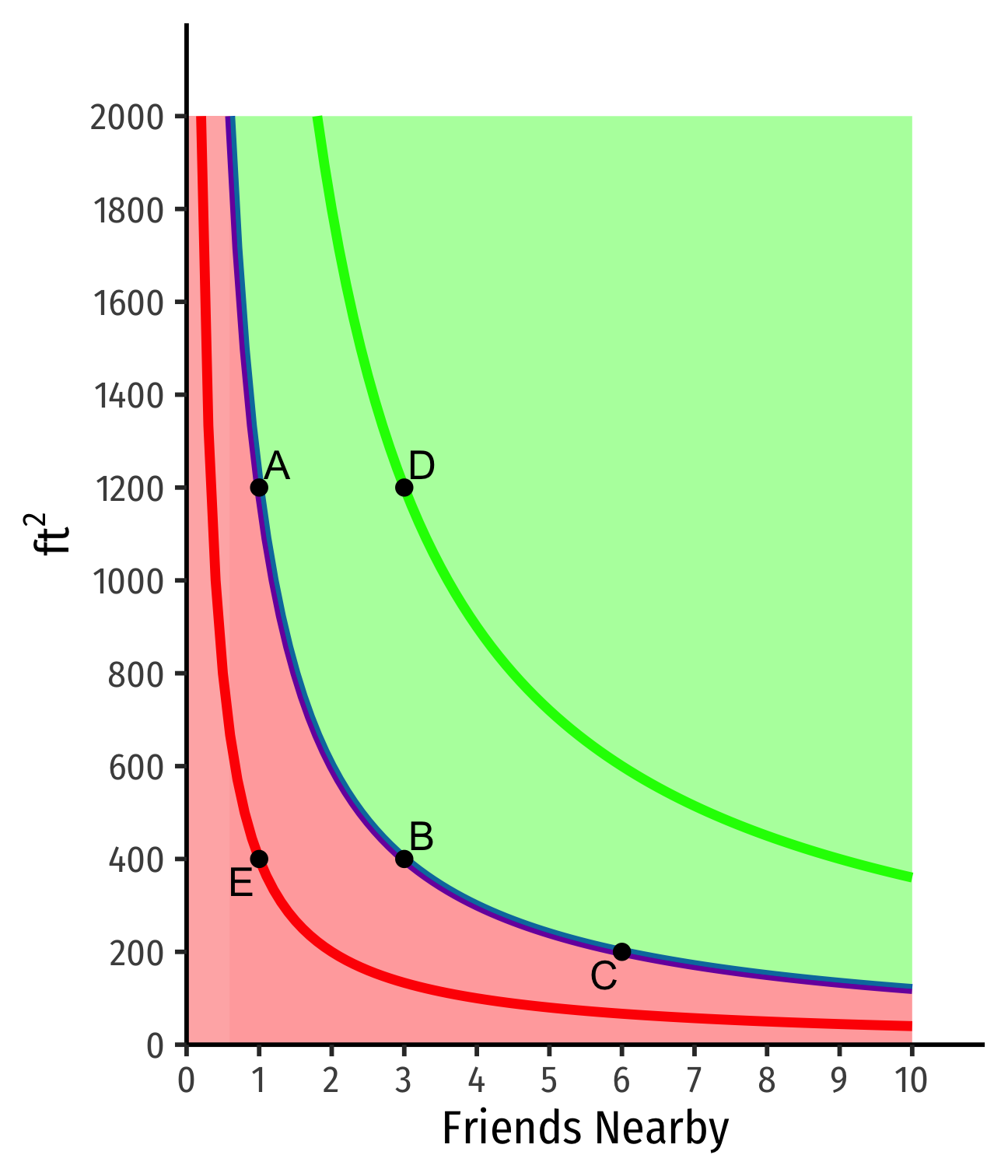
Indifference Curves: Example
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
Indifferent between all apts on the same curve
Apts above curve are preferred over apts on curve
- D≻A∼B∼C
- Actually on a higher curve
Apts below curve are preferred less than apts on curve
- E≺A∼B∼C
- Actually on a lower curve
Assumptions About Indifference Curves
- Like preferences, indifference curves are "well-behaved" when:
We can always draw indifference curves: two bundles can always be ranked
Monotonic: "more is preferred to less"
Convex: "averages are preferred to extremes"
Indifference curves can never cross: preferences are transitive
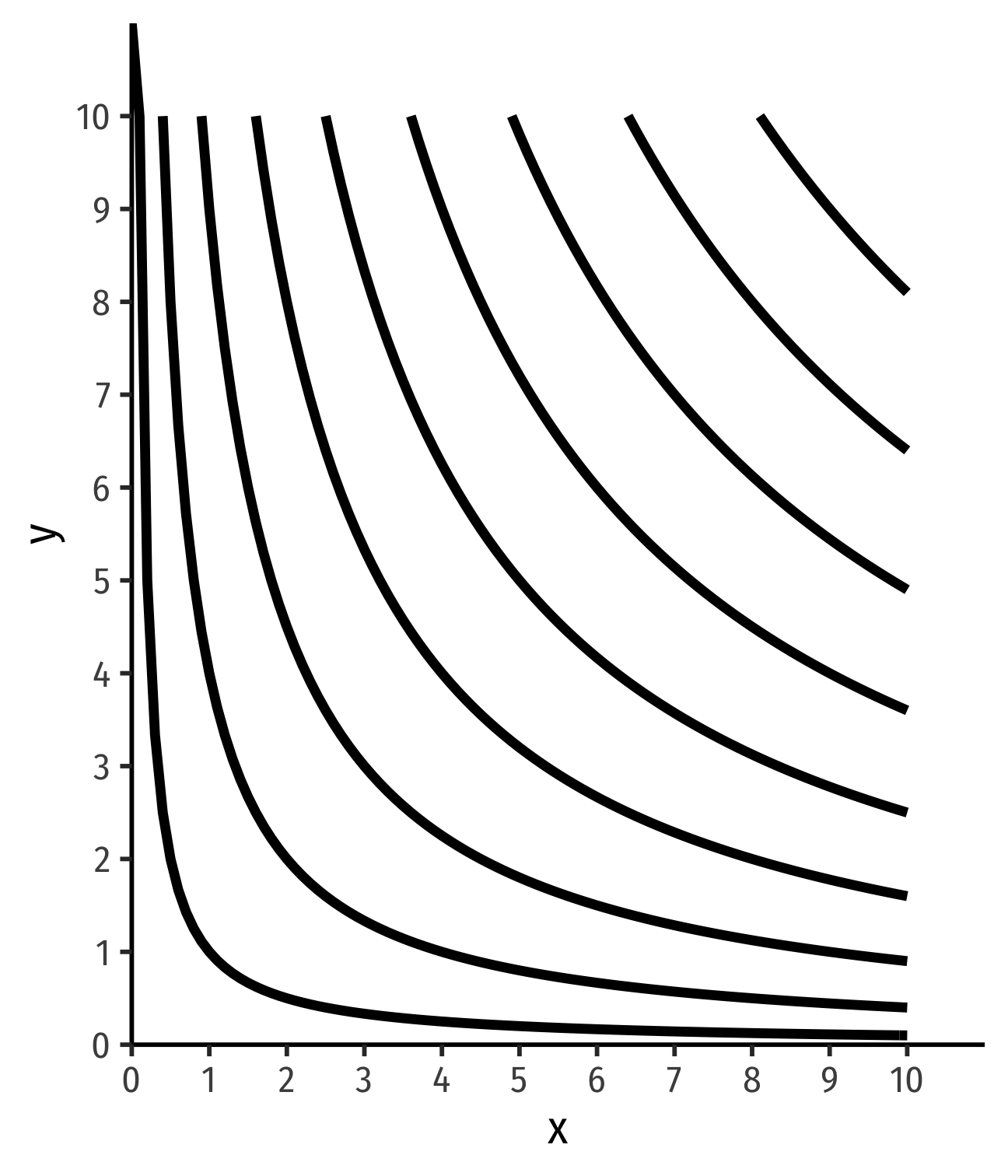
Assumption 1: We Can Always Draw Them
We can always draw indifference curves: two bundles can always be ranked
Every possible bundle (point on graph) is on an indifference curve
Assumption 1: We Can Always Draw Them
We can always draw indifference curves: two bundles can always be ranked
Every possible bundle (point on graph) is on an indifference curve
Assumption 2: Monotonicity
Monotonic: "more is preferred to less"
For any bundle b with more of at least one good than bundle a⟹a≺b
Moves to NE always preferable
Moves to SW always unpreferable
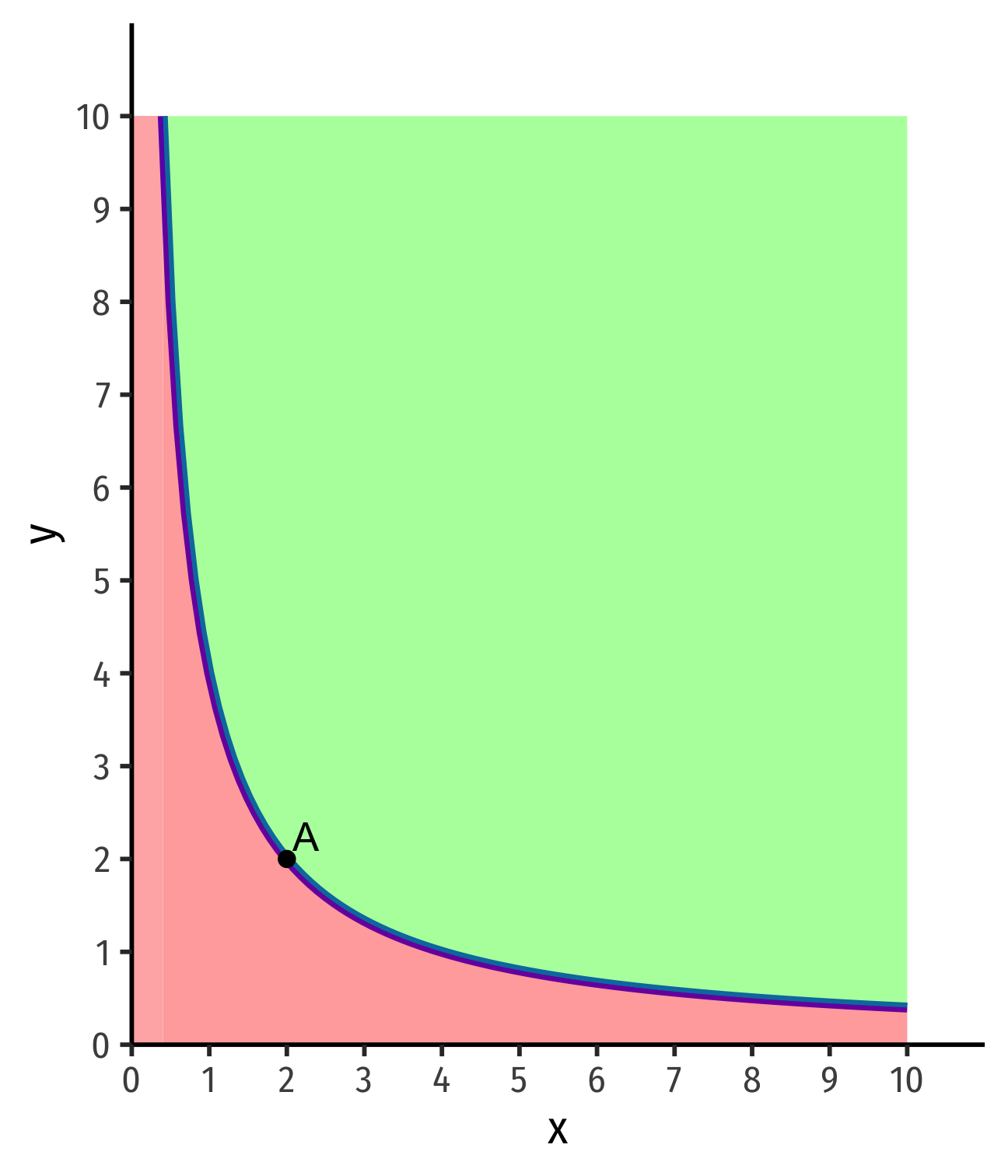
Assumption 3: Convexity
Convex: "averages are preferred to extremes"
Take a (weighted) average of any two apartments on curve
Any apt that provides a "balance" of the two desired goods (e.g. C)≺ "unbalanced" (A or B)
Observation: people prefer variety in consumption
Mathematically:1 convex ⟹ a line connecting two points on function lies above the function
1 f(wx1+(1−w)x2)<wf(x1)+(1−w)f(x2)∀w∈[0,1]
Assumption 4: Curves Never Cross
Indifference curves can never cross: preferences are transitive
Suppose two curves crossed:
A∼B
B∼C
But C ≻ B!
Preferences are not transitive!
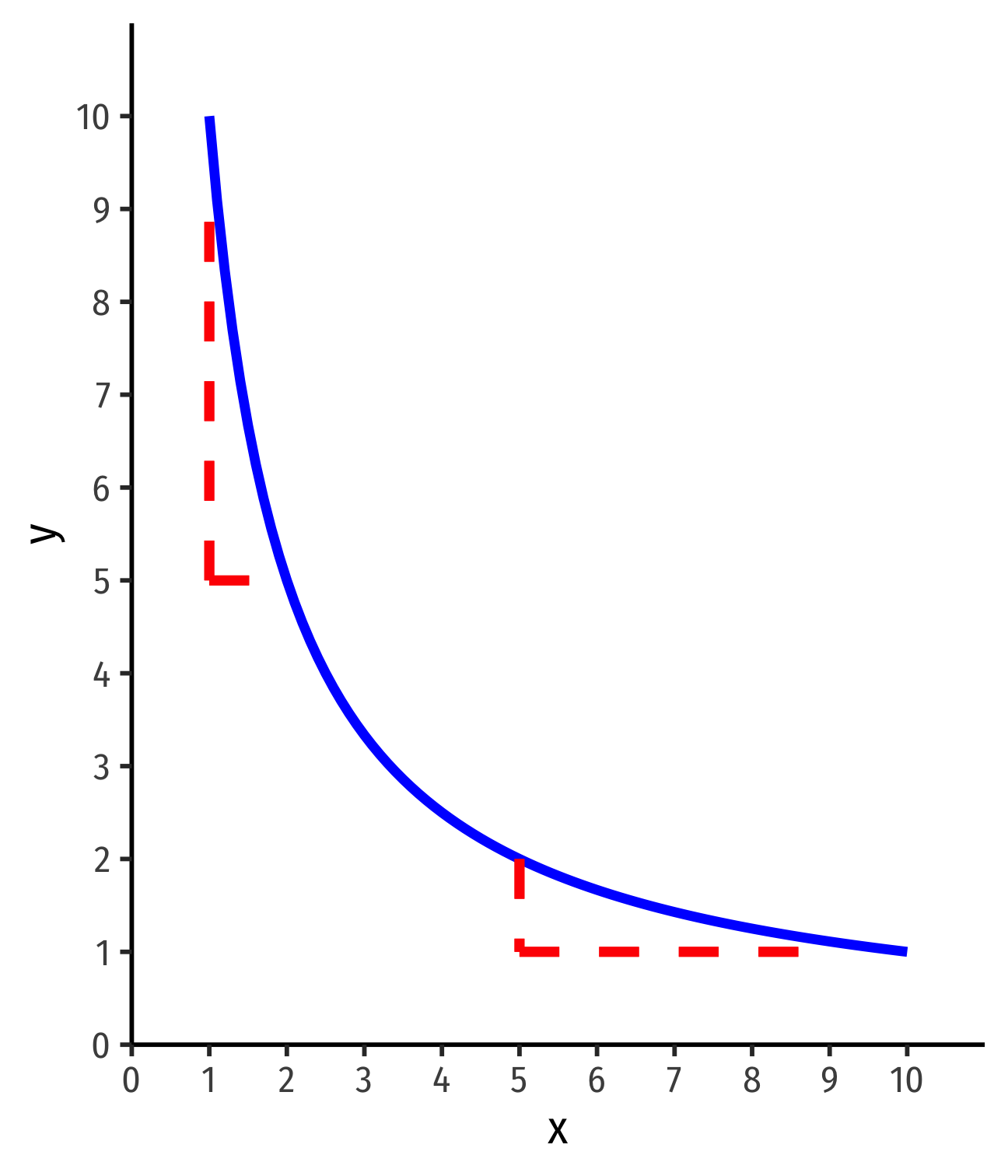
Marginal Rate of Substitution I
If I take away one friend nearby, how many more ft2 would you need to keep you indifferent?
Marginal Rate of Substitution (MRS): rate at which you trade off one good for the other and stay satisfied (remain indifferent)
Think of this as the opportunity cost: # of units of y you need to give up to acquire 1 more x
Recall, budget constraint measures market-valued trade off between x and y
MRS measures your personal evaluation of x vs. y based on your preferences
Marginal Rate of Substitution I
If I take away one friend nearby, how many more ft2 would you need to keep you indifferent?
Marginal Rate of Substitution (MRS): rate at which you trade off one good for the other and stay satisfied (remain indifferent)
Think of this as the opportunity cost: # of units of y you need to give up to acquire 1 more x
Recall, budget constraint measures market-valued trade off between x and y
MRS measures your personal evaluation of x vs. y based on your preferences
- Foreshadowing: what if they are different? Are you truly maximizing your preferences?
Marginal Rate of Substitution II
MRS is the slope of the indifference curve MRSx,y=−ΔyΔx=riserun
Amount of y given up for 1 more x
Note: slope (MRS) changes along the curve!
So Where are the Numbers?
Long ago (1890s), utility considered a real, measurable, cardinal scale1
Utility thought to be lurking in people's brains
- Could be understood from first principles: calories, water, warmth, etc
Obvious problems
1 "Neuroeconomics" & cognitive scientists are re-attempting a scientific approach to measure utility
Utility Functions?
20th century innovation: preferences as the objects of maximization
We can plausibly measure preferences via implications of peoples' actions!
Principle of Revealed Preference: if x and y are both feasible, and if x is chosen over y, then the person must (weakly) prefer x⪰y
Flawless? Of course not. But extremely useful!
Utility Functions! I
So how can we build a function to "maximize preferences"?
Construct a utility function u(⋅)1 that represents preference relations (≻,≺,∼)
Assign utility numbers to bundles, such that, for any bundles a and b: a≻b⟺u(a)>u(b)
1 The ⋅ is a placeholder for whatever goods we are considering (e.g. x, y, burritos, lattes, etc)
Utility Functions! II
We can model "as if" the consumer is maximizing utility/preferences by maximizing the utility function:
"Maximizing preferences" : choosing a such that a≻b for all available b
"Maximizing utility" : choosing a such that u(a)>u(b) for all available b
Identical if they contain the same information
1 The (\cdot) is a placeholder for whatever goods we are considering (e.g. (x), (y), (burritos), (lattes), etc)
Utility Functions, Pural I
- Imagine three alternative bundles of (x,y):
a=(1,2)b=(2,2)c=(4,3)
Utility Functions, Pural I
Imagine three alternative bundles of (x,y): a=(1,2)b=(2,2)c=(4,3)
Create a utility function u(⋅) that assigns each bundle a utility level of
| u(⋅) |
|---|
| u(a)=1 |
| u(b)=2 |
| u(c)=3 |
- Does it mean that bundle c is 3 times the utility of a?
Utility Functions, Pural I
Imagine three alternative bundles of (x,y): a=(1,2)b=(2,2)c=(4,3)
Create a utility function u(⋅) that assigns each bundle a utility level of
| u(⋅) |
|---|
| u(a)=1 |
| u(b)=2 |
| u(c)=3 |
- Does it mean that bundle c is 3 times the utility of a?
Utility Functions, Pural II
Imagine three alternative bundles of (x,y): a=(1,2)b=(2,2)c=(4,3)
Now consider u(⋅) and a second utility function v(⋅):
| u(⋅) | v(⋅) |
|---|---|
| u(a)=1 | v(a)=3 |
| u(b)=2 | v(b)=5 |
| u(c)=3 | v(c)=7 |
Utility Functions, Pural III
Utility numbers have an ordinal meaning only, not cardinal
Only the preference ordering* of a,b,c matters!
Both are valid:1
- u(c)>u(b)>u(a)
- w(c)>w(b)>w(a)
Because c≻b≻a
1 See the Mathematical Appendix in Today's Class Page for why.