+ - 0:00:00
Notes for current slide
Notes for next slide

1.3: Constrained Optimization and the Budget Constraint

ECON 306 · Microeconomic Analysis · Fall 2019

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microf19
microF19.classes.ryansafner.com

The Two Major Models of Economics as a "Science"

Optimization

  • Agents have objectives they value

  • Agents face constraints

  • Make tradeoffs to maximize objectives within constraints

The Two Major Models of Economics as a "Science"

Optimization

  • Agents have objectives they value

  • Agents face constraints

  • Make tradeoffs to maximize objectives within constraints

Equilibrium

  • Agents face competition from others that affect prices

  • Agents adjust their behaviors based on prices

  • Stable outcomes result where all agents cease adjusting

Individual Choice

Consumer Behavior

  • How do people decide:

    • which products to buy
    • which activities to dedicate their time to
    • how to save or invest/plan for the future

  • A model of behavior we can extend to most scenarios

  • Answers to these questions are building blocks for demand curves

Individuals and Consumers

  • Everyone is a consumer

    • Recall we need not limit "goods and services" to food, clothing, etc. - theyr are anything that you value!

  • Consumers making purchasing decisions will be our paradigmatic example

    • But we are really talking about how individuals make choices in almost any context!

Constrained Optimization

Constrained Optimization I

  • We model most situations as a constrained optimization problem:

  • People optimize: make tradeoffs to achieve their objective as best as they can

  • Subject to constraints: limited resources (income, time, attention, etc)

Constrained Optimization II

  • One of the most generally useful mathematical models

  • Endless applications: how we model nearly every decision-maker

consumer, business firm, politician, judge, bureaucrat, voter, dictator, pirate, drug cartel, drug addict, parent, child, etc

  • Key economic skill: recognizing how to apply the model to a situation

  • Luckily, all models have a common setup...

Constrained Optimization III

  • All constrained optimization models have three moving parts:

Constrained Optimization III

  • All constrained optimization models have three moving parts:
  1. Choose: < some alternative >

Constrained Optimization III

  • All constrained optimization models have three moving parts:

  1. Choose: < some alternative >

  2. In order to maximize: < some objective >

Constrained Optimization III

  • All constrained optimization models have three moving parts:

  1. Choose: < some alternative >

  2. In order to maximize: < some objective >

  3. Subject to: < some constraints >

Constrained Optimization: Example I

Example: A Hood student picking courses hoping to achieve the highest GPA while getting an Econ major.

  1. Choose:

  2. In order to maximize:

  3. Subject to:

Constrained Optimization: Example II

Example: How should FedEx plan its delivery route?

  1. Choose:

  2. In order to maximize:

  3. Subject to:

Constrained Optimization: Example III

Example: The U.S. government wants to remain economically competitive but reduce emissions by 25%.

  1. Choose:

  2. In order to maximize:

  3. Subject to:

Constrained Optimization: Example IV

Example: How do elected officials make decisions in politics?

  1. Choose:

  2. In order to maximize:

  3. Subject to:

The Consumer's Problem

  • The consumer's constrained optimization problem is:

The Consumer's Problem

  • The consumer's constrained optimization problem is:
  1. Choose: < a consumption bundle >

The Consumer's Problem

  • The consumer's constrained optimization problem is:

  1. Choose: < a consumption bundle >

  2. In order to maximize: < utility >

The Consumer's Problem

  • The consumer's constrained optimization problem is:

  1. Choose: < a consumption bundle >

  2. In order to maximize: < utility >

  3. Subject to: < income and market prices >

Consumer Behavior: Basic Framework

Consumption Bundles

  • Imagine a (very strange) supermarket sells xylophones (x) and yams (y)

  • Your choices: amounts of x,y to buy as a bundle

Consumption Bundles

  • Imagine a (very strange) supermarket sells xylophones (x) and yams (y)

  • Your choices: amounts of x,y to buy as a bundle

  • We can represent your choices as a vector:

a=(xy)

Consumption Bundles

  • Imagine a (very strange) supermarket sells xylophones (x) and yams (y)

  • Your choices: amounts of x,y to buy as a bundle

  • We can represent your choices as a vector:

a=(xy)

Examples:

a=(412);b=(612);c=(210)

Consumption Bundles: Graphically

  • We can represent choices graphically

  • We'll stick with 2 goods (x,y) in 2-dimensions

The Budget Constraint

Affordability

  • If you had $100 to spend, what bundles of goods {x,y} would you buy?

  • Only those bundles that are affordable

  • Denote prices of each good as {px,py}

  • Let m be the amount of income a consumer has

Affordability

  • If you had $100 to spend, what bundles of goods {x,y} would you buy?

  • Only those bundles that are affordable

  • Denote prices of each good as {px,py}

  • Let m be the amount of income a consumer has

  • A consumption bundle {x,y} is affordable at given prices {px,py} when:

pxx+pyy≤m

The Budget Set

  • The set of all affordable bundles that a consumer can choose is called the budget set or choice set

pxx+py≤m

  • The budget constraint is the set of all bundles that spend all income m:1

pxx+pyy=m

1 Note the difference (the in/equality), budget constraint is the subset of the budget set that spends all income.

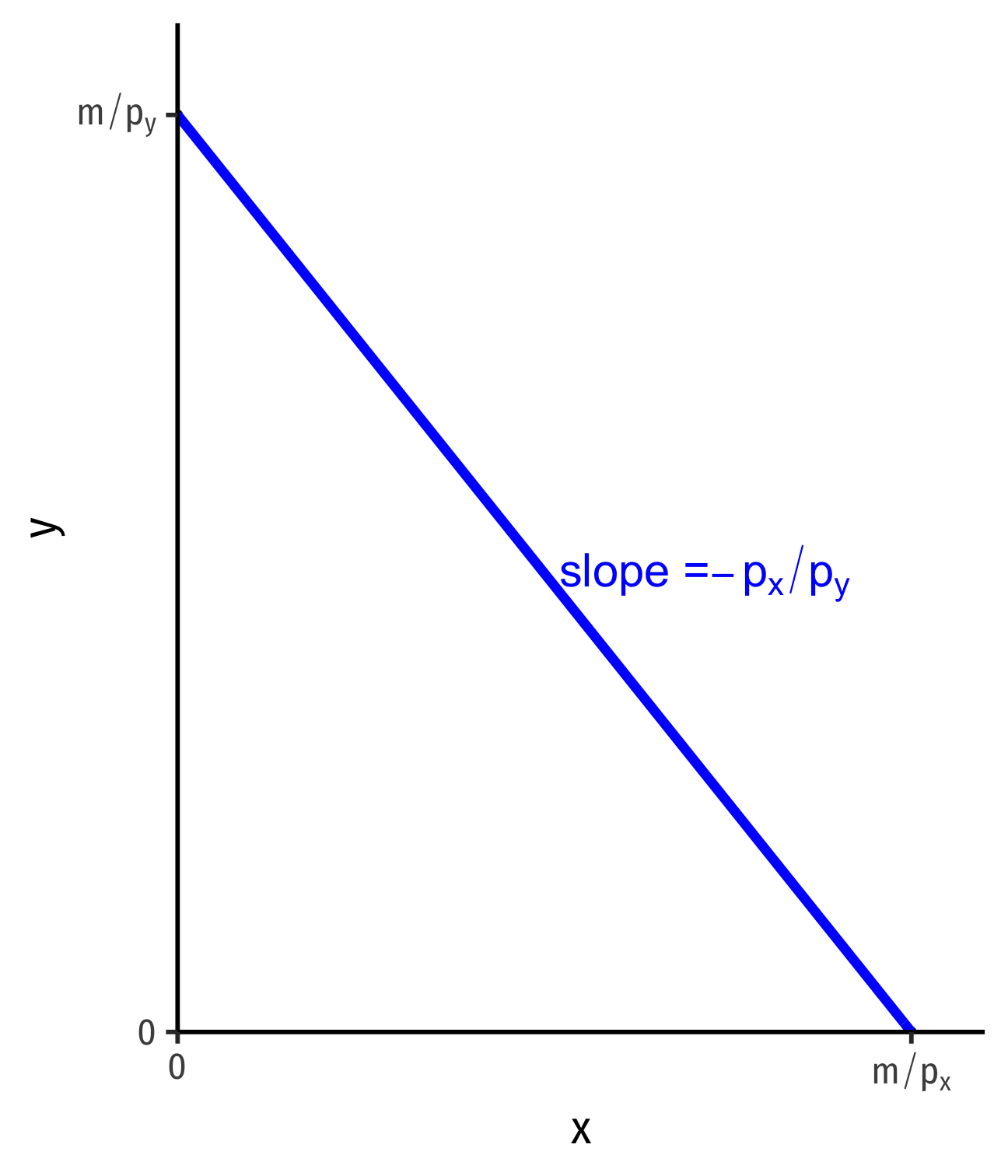
The Budget Constraint, Graphically

  • For 2 goods, (x,y)

pxx+pyy=m

The Budget Constraint, Graphically

  • For 2 goods, (x,y)

pxx+pyy=m

  • Solve for y to graph

y=mpy−pxpyx

The Budget Constraint, Graphically

  • For 2 goods, (x,y)

pxx+pyy=m

  • Solve for y to graph

y=mpy−pxpyx

  • y-intercept: mpy
  • x-intercept: mpx

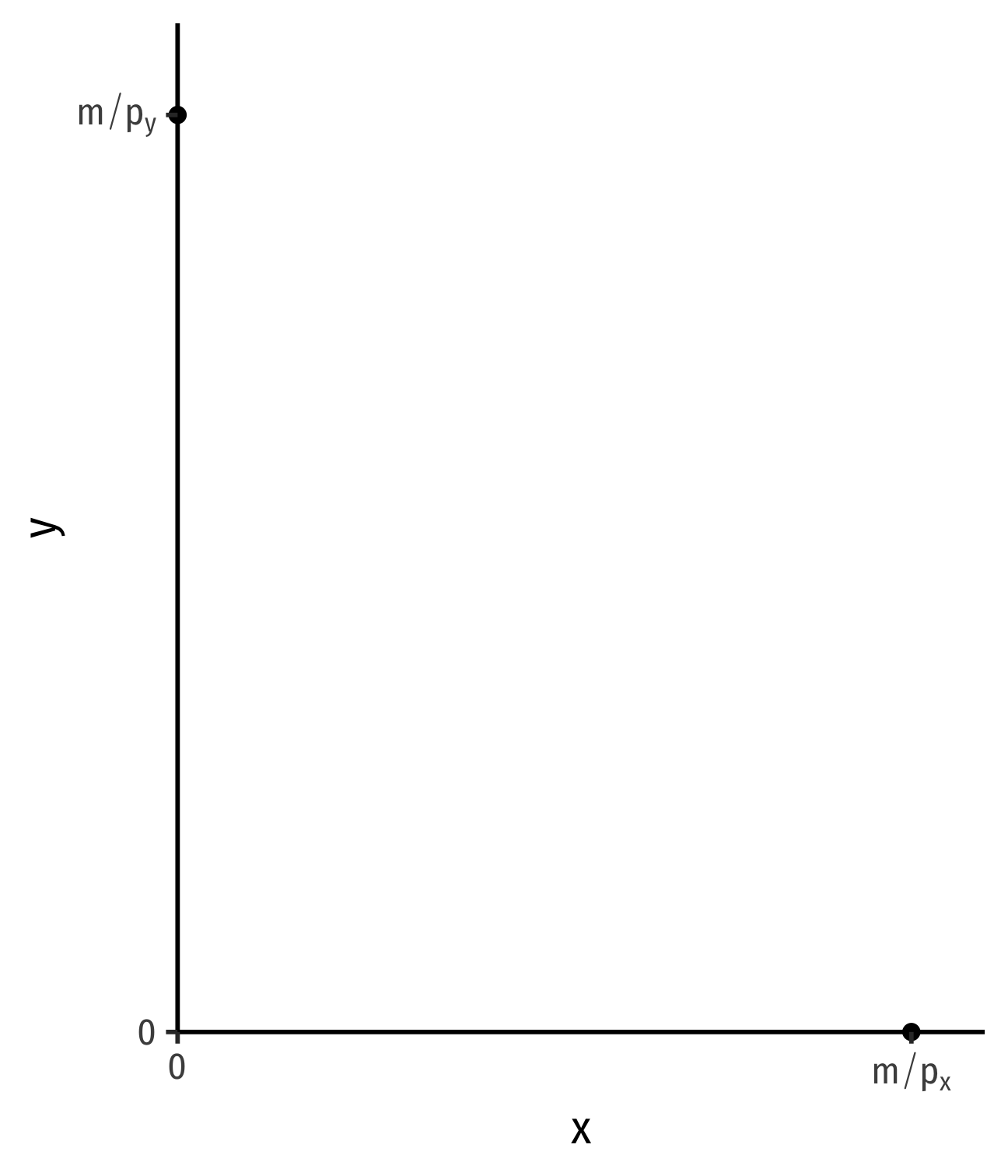
The Budget Constraint, Graphically

  • For 2 goods, (x,y)

pxx+pyy=m

  • Solve for y to graph

y=mpy−pxpyx

  • y-intercept: mpy
  • x-intercept: mpx
  • slope: −pxpy

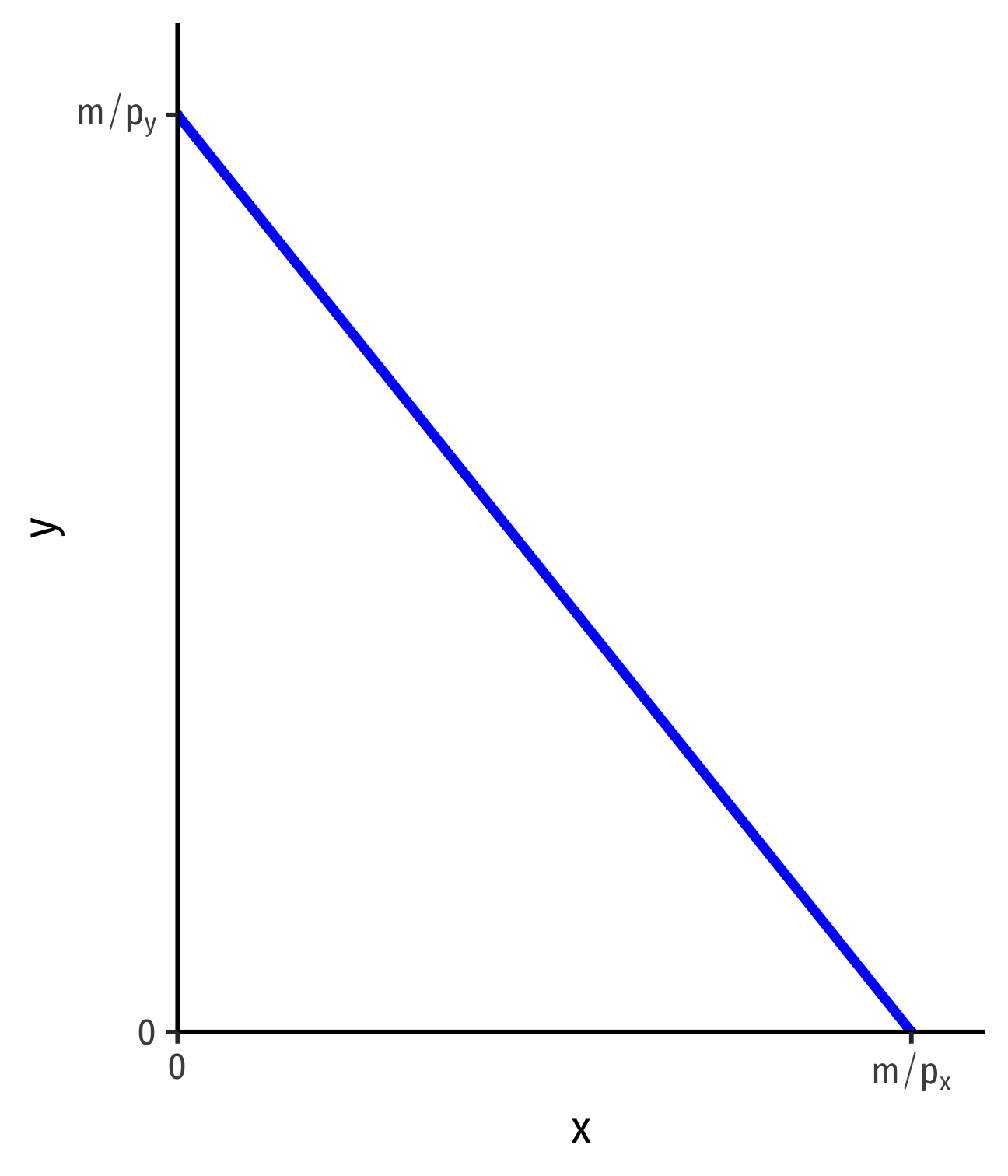
The Budget Constraint, Graphically

  • For 2 goods, (x,y)

pxx+pyy=m

  • Solve for y to graph

y=mpy−pxpyx

  • y-intercept: mpy
  • x-intercept: mpx

  • slope: pxpy

  • Budget constraint is the upper limit of the budget set

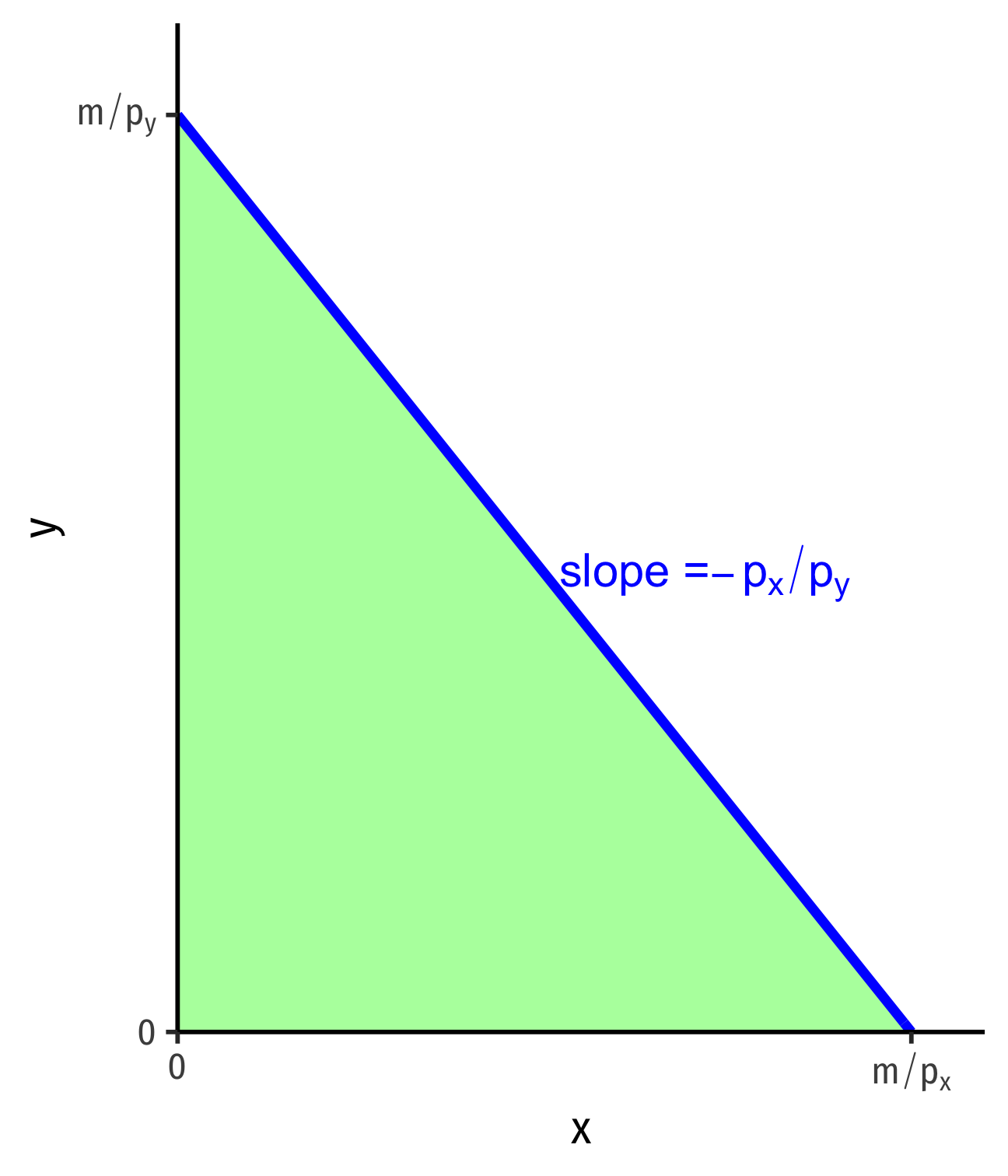
The Budget Constraint: Example

Example: Suppose you have an income of $50 to spend on lattes (l) and burritos (b). The price of lattes is $5 and the price of burritos is $10. Let l be on the horizontal axis and b be on the vertical axis.

  1. Write an equation for the budget constraint (in graphable form).

  2. Graph the budget constraint.

Interpreting the Budget Constraint

  • Points on the line spend all income
    • A: $5(0x)+$10(5y)=$50
    • B: $5(10x)+$10(0y)=$50
    • C: $5(2x)+$10(4y)=$50
    • D: $5(6x)+$10(2y)=$50

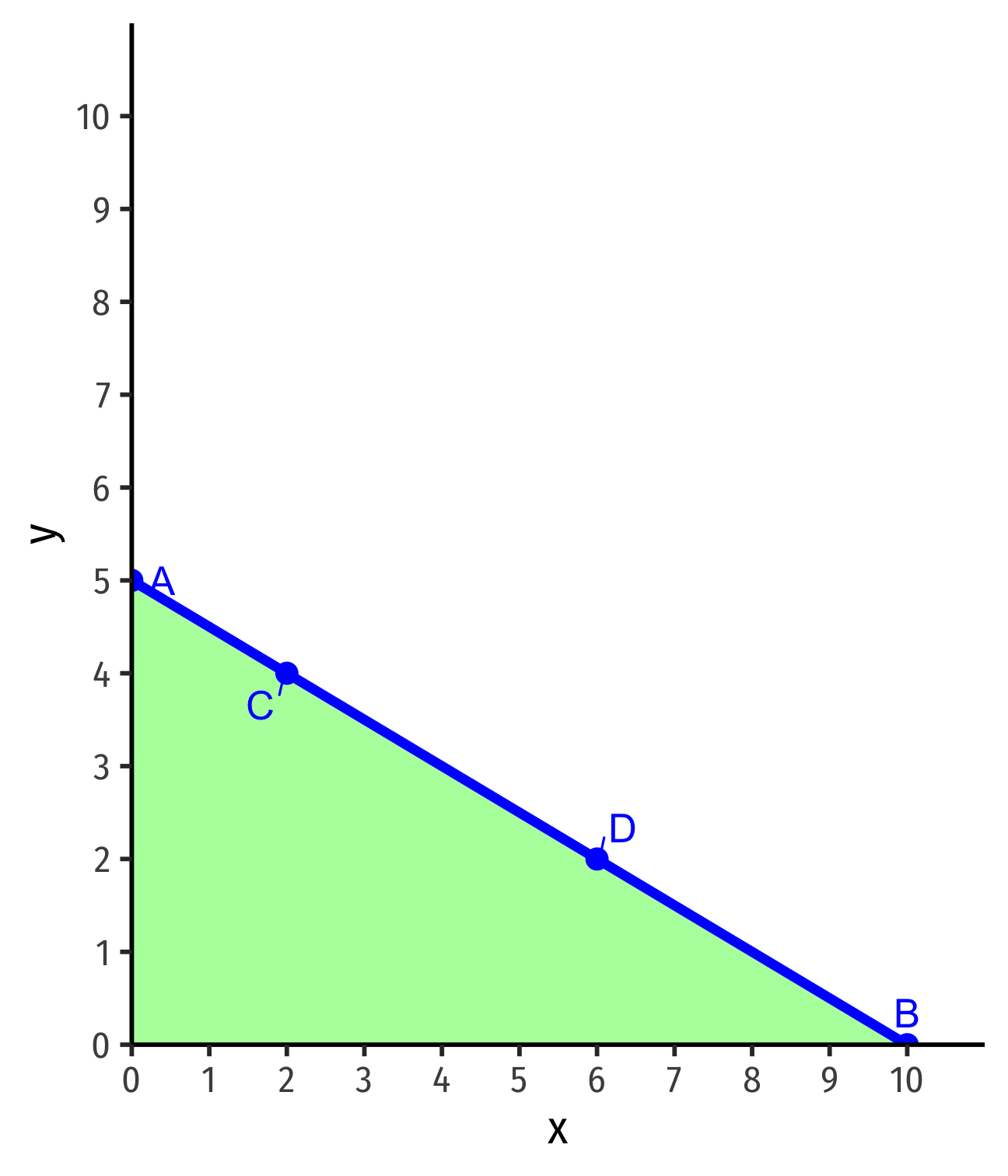
Interpreting the Budget Constraint

  • Points on the line spend all income

    • A: $5(0x)+$10(5y)=$50
    • B: $5(10x)+$10(0y)=$50
    • C: $5(2x)+$10(4y)=$50
    • D: $5(6x)+$10(2y)=$50

  • Points beneath the line are affordable (in the budget set) but don't use all income

    • E: $5(3x)+$10(2y)=$35

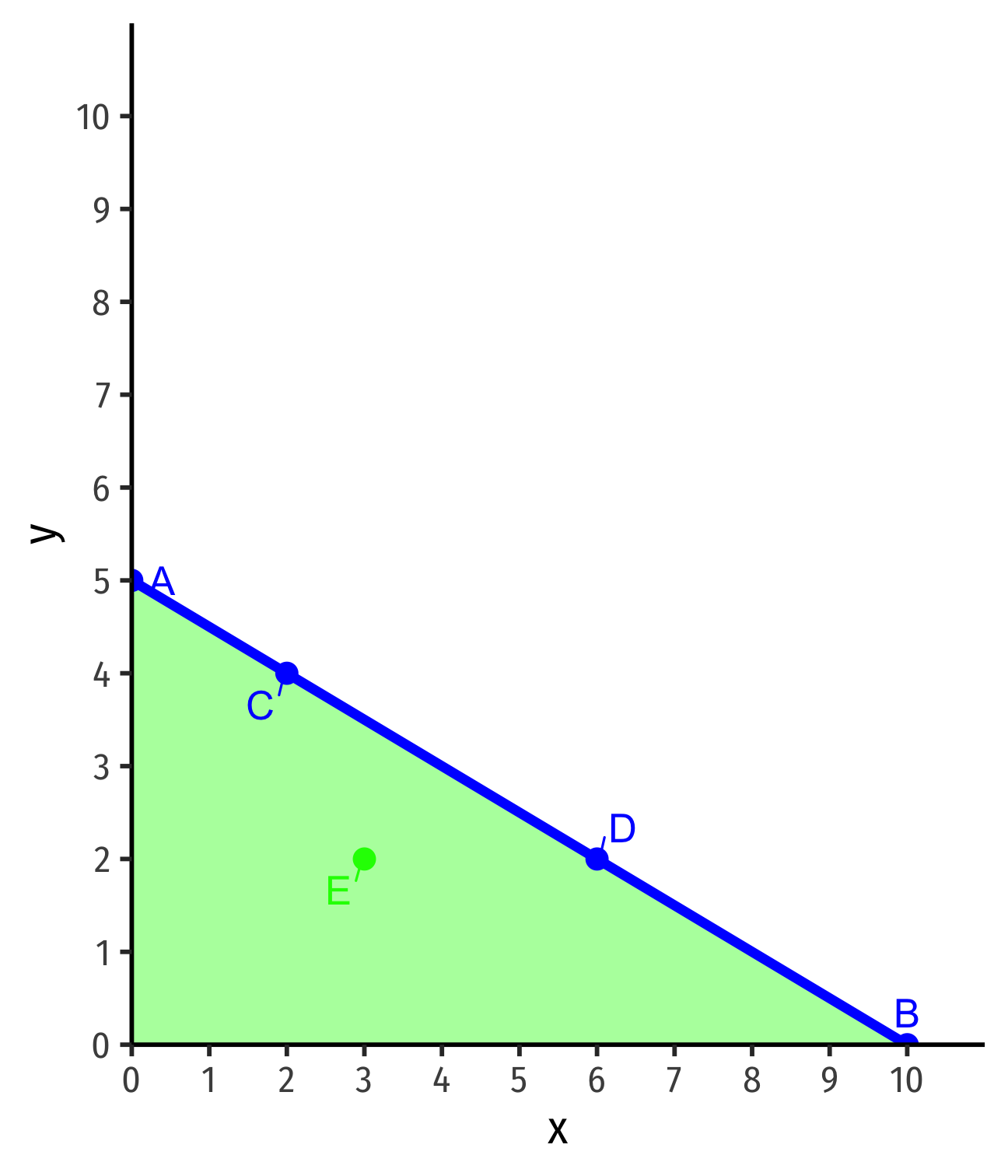
Interpreting the Budget Constraint

  • Points on the line spend all income

    • A: $5(0x)+$10(5y)=$50
    • B: $5(10x)+$10(0y)=$50
    • C: $5(2x)+$10(4y)=$50
    • D: $5(6x)+$10(2y)=$50

  • Points beneath the line are affordable (in the budget set) but don't use all income

    • E: $5(3x)+$10(2y)=$35

  • Points above the line are unaffordable (at current income and prices)

    • F: $5(6x)+$10(4y)=$70

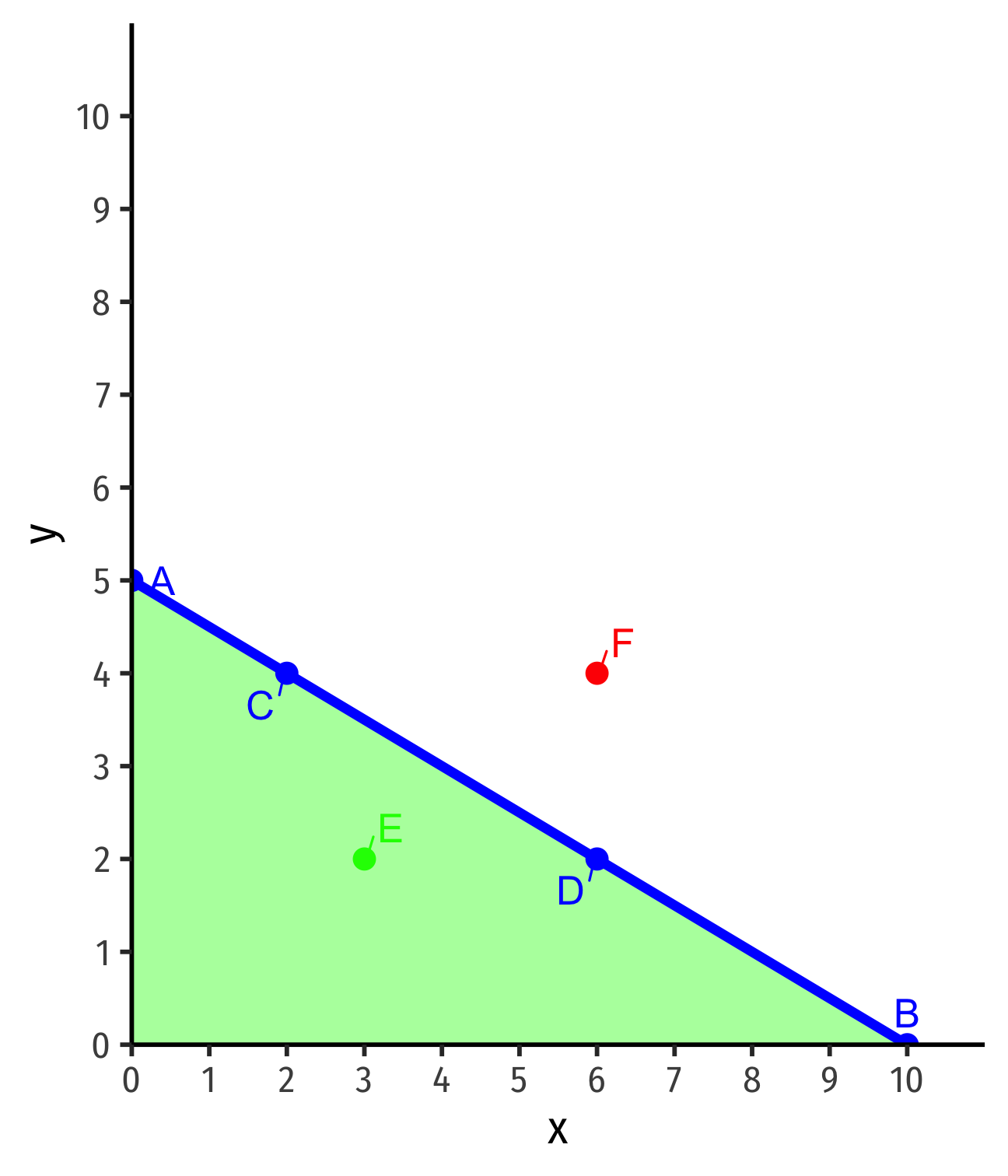
Interpretting the Slope

  • Slope: market-rate of tradeoff between x and y

  • Relative price of x or opportunity cost of x:

Consuming 1 more unit of x requires giving up pxpy units of y

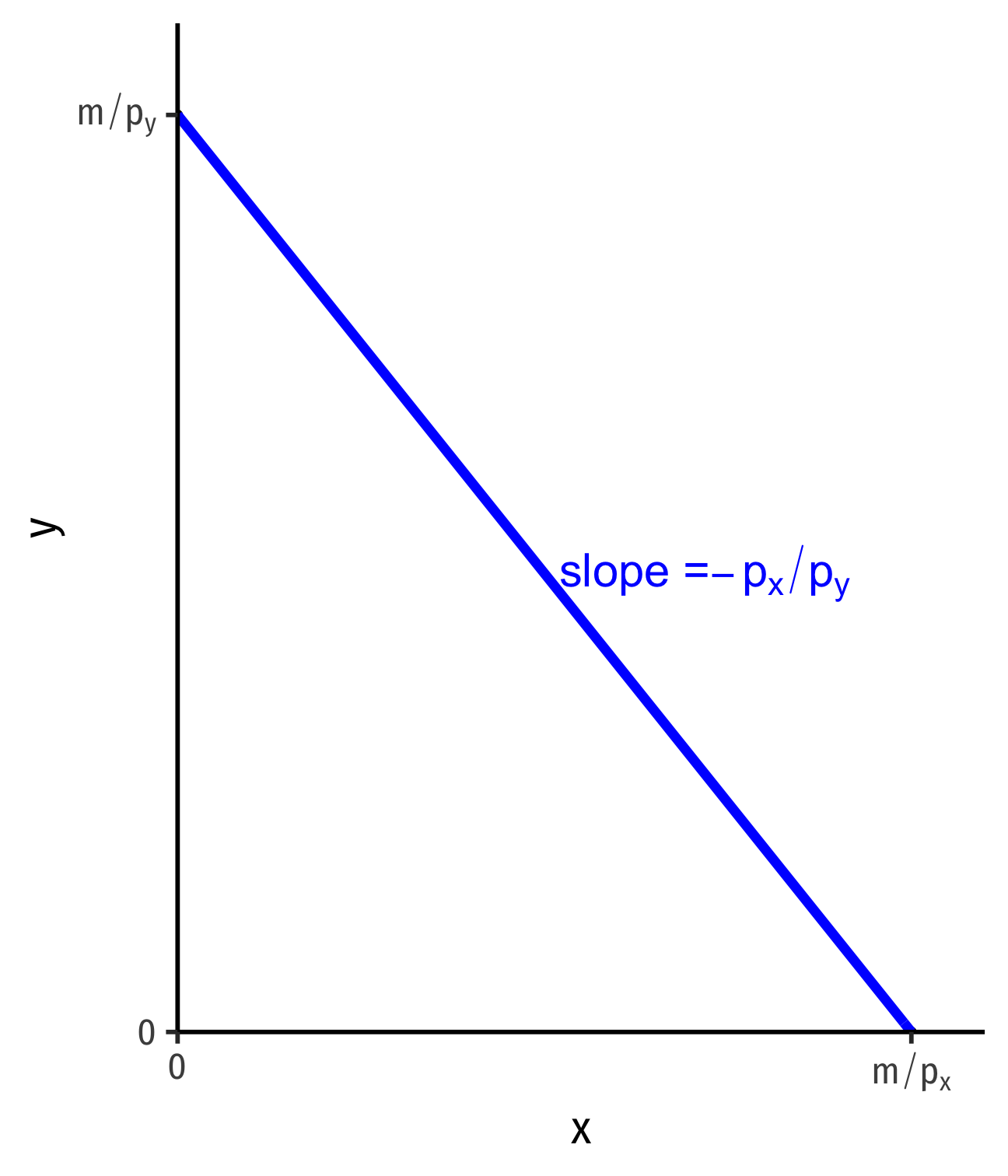
Interpretting the Slope

  • Slope: market-rate of tradeoff between x and y

  • Relative price of x or opportunity cost of x:

Consuming 1 more unit of x requires giving up pxpy units of y

  • Foreshadowing:

Is your valuation of the tradeoff between x and y the same as the market rate?

Changes in Parameters

Changes in Parameters

m=pxx+pyyy=mpy−pxpyx

  • Budget constraint is a function of specific parameters

    • m: income
    • px,py: market prices

  • What happens to the budget constraint as these change?

  • Where economics begins: how changes in constraints affect people's choices

Changes in Income, m

  • Changes in income: a parallel shift in budget constraint

Example: An increase in income

  • Same slope (relative prices don't change!)

  • Gain of affordable bundles

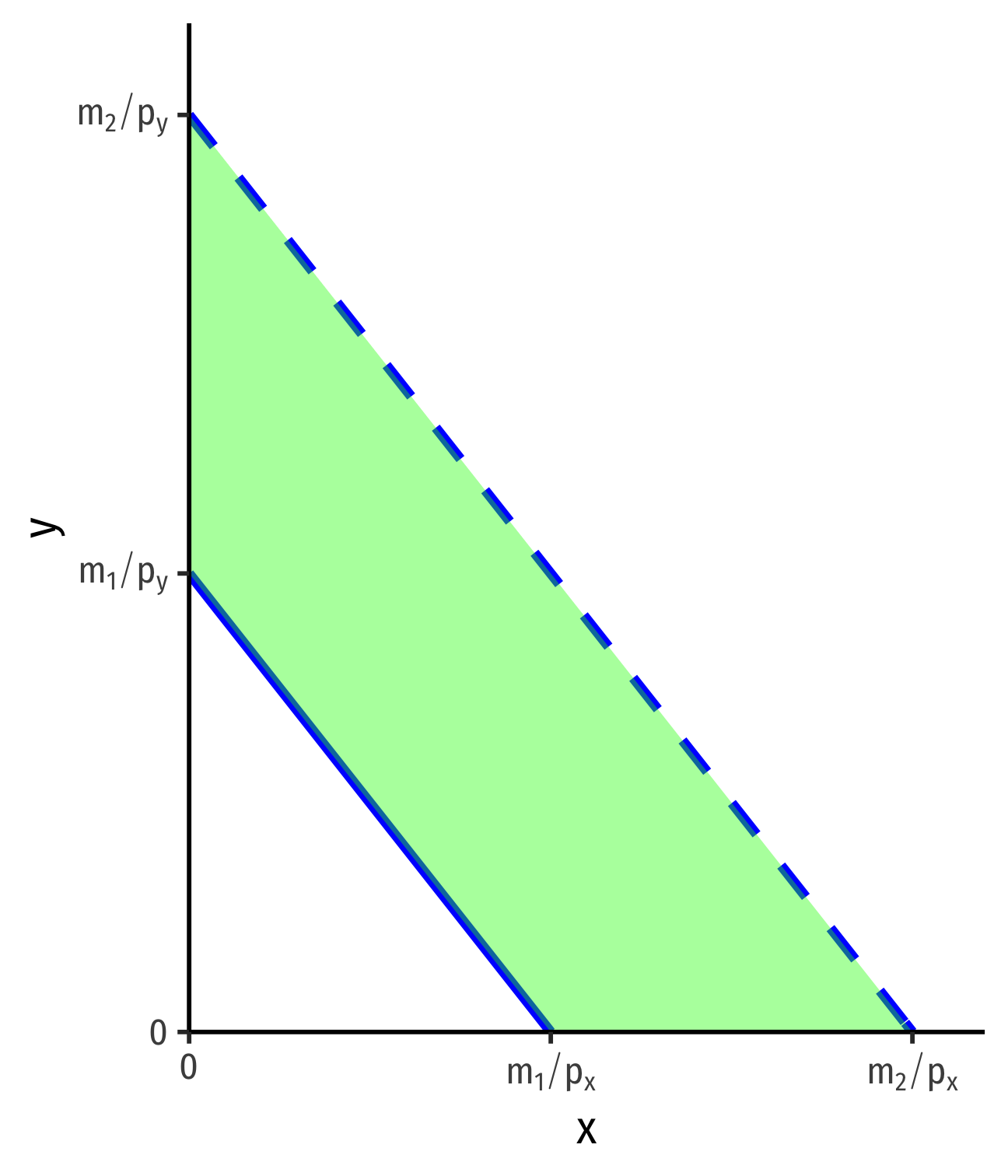
Changes in Income, m: Example

Example: Continuing the lattes and burritos example, (income is $50, lattes are $5, burritos are $10), suppose your income doubles to $100.

  1. Find the equation of the new budget constraint (in graphable form).

  2. Graph the new budget constraint.

Changes in Relative Prices, px or py

  • Changes in relative prices: rotate the budget constraint

Example: An increase in the price of x

  • Slope steepens: −p′xpy

  • Loss of affordable bundles

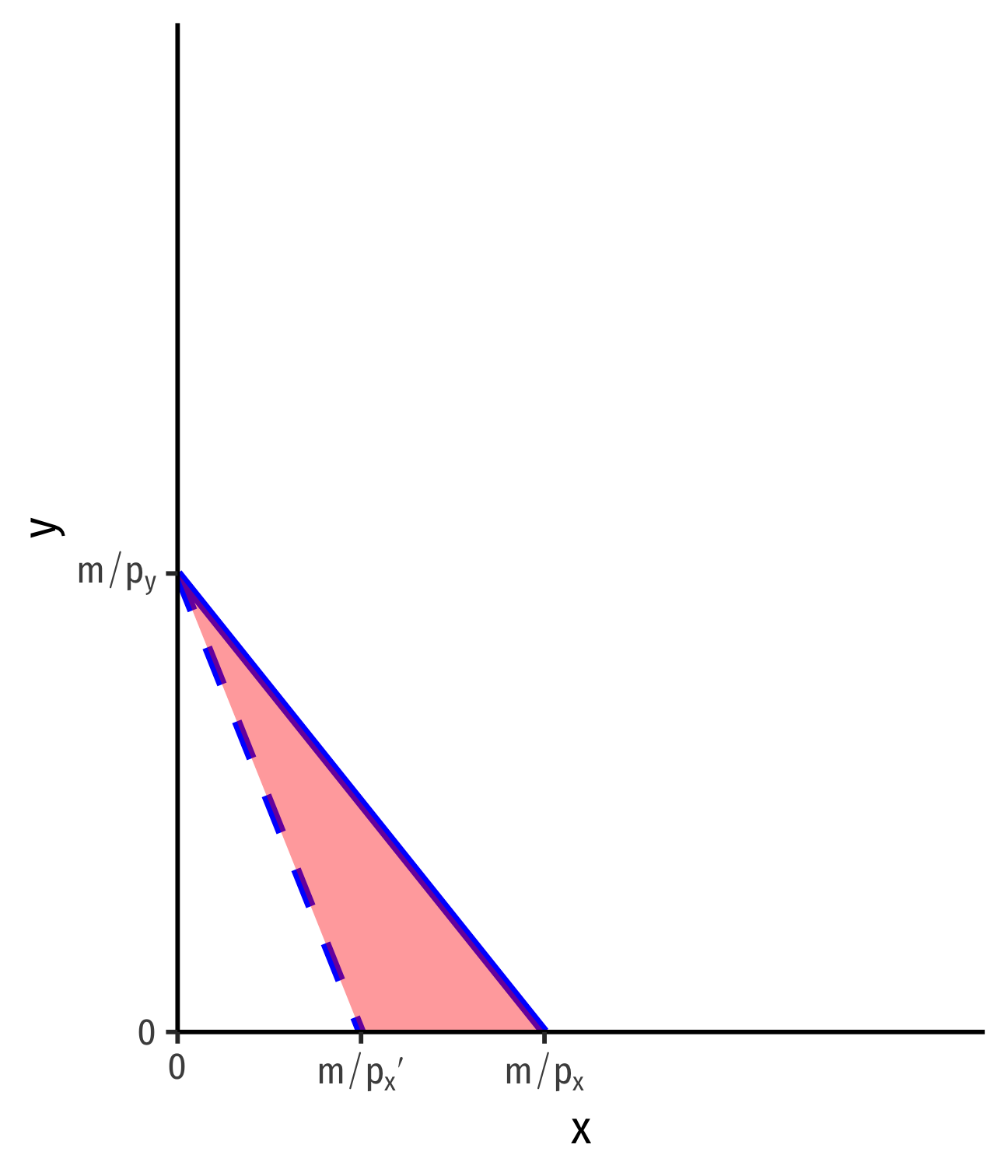
Changes in Relative Prices, px or py

  • Changes in relative prices: rotate the budget constraint

Example: A decrease in the price of y

  • Slope flattens: −pxp′y

  • Gain of affordable bundles

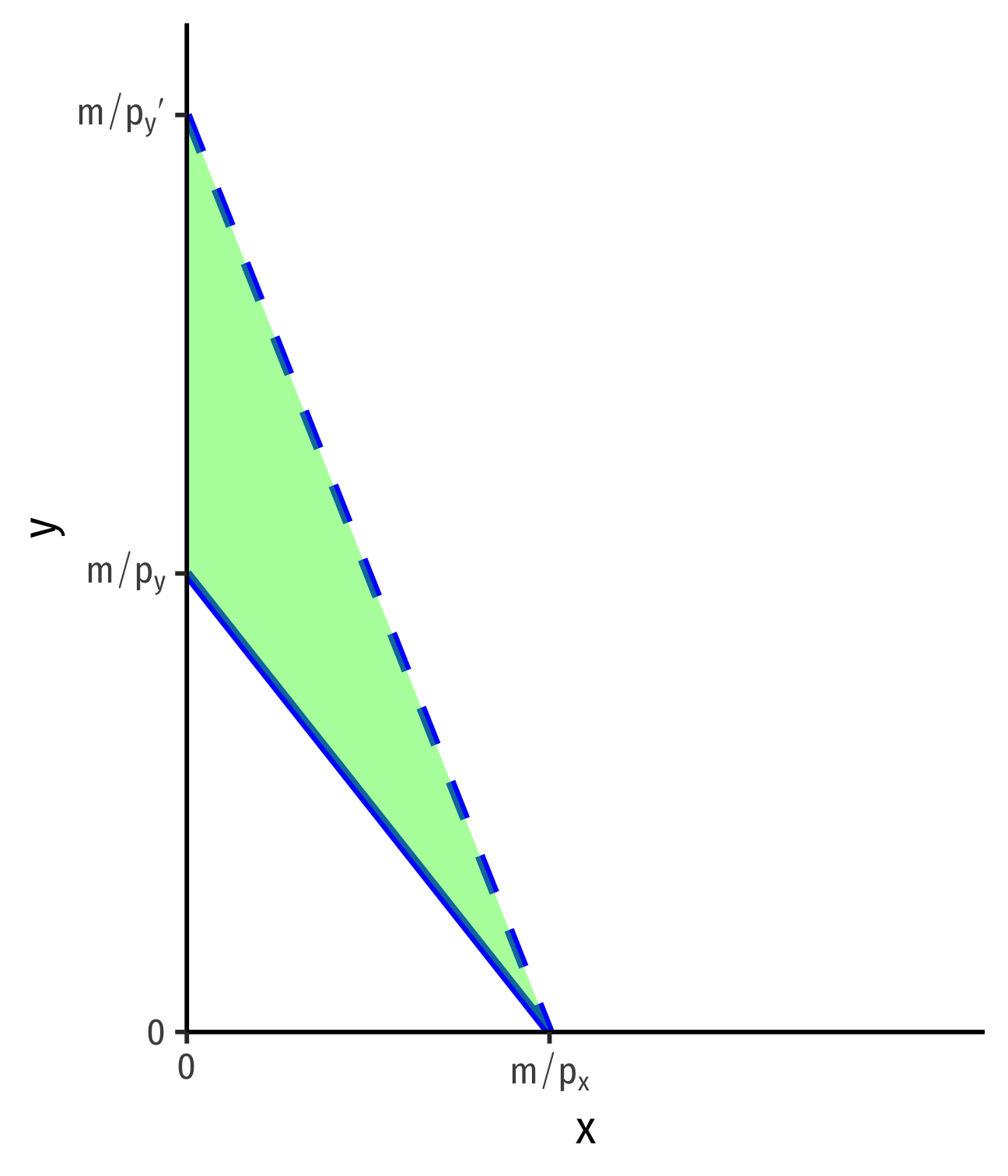
Economics is About (Changes in) Relative Prices

  • Economics is about (changes in) relative prices

  • Budget constraint slope is (pxpy)

  • Only "real" changes in relative prices (from changes in market valuations) change consumer constraints

  • "Nominal" prices are often meaningless!

Economics is About (Changes in) Relative Prices

  • Economics is about (changes in) relative prices

  • Budget constraint slope is (pxpy)

  • Only "real" changes in relative prices (from changes in market valuations) change consumer constraints

  • "Nominal" prices are often meaningless!

Example: Imagine yourself in a strange country. All you know is that the price of bread is "6"...

Economics is About (Changes in) Relative Prices

  • Economics is about (changes in) relative prices

  • Budget constraint slope is (pxpy)

  • Only "real" changes in relative prices (from changes in market valuations) change consumer constraints

  • "Nominal" prices are often meaningless!

Example: Imagine yourself in a strange country. All you know is that the price of bread is "6"...

  • If all prices & incomes changed at the same rate...what would happen in real terms?

Changes in Relative Prices: Example

Example: Continuing the lattes and burritos example (income is $50, lattes are $5, burritos are $10).

  1. Suppose the price of lattes doubles from $5 to $10. Find the equation of the new budget constraint and graph it.

  2. Return to the original price of lattes ($5) and suppose the price of burritos falls from $10 to $5. Find the equation of the new budget constraint and graph it.

Applications of Budget Constraints

Application I: Which is better, a gift in kind, or cash? Relatedly - which policy is better, giving low income groups access to specific goods, or them giving cash?

Applications of Budget Constraints

Application I: Which is better, a gift in kind, or cash? Relatedly - which policy is better, giving low income groups access to specific goods, or them giving cash?

Application II: Are Cadillacs cheaper for professors than for students?

The Two Major Models of Economics as a "Science"

Optimization

  • Agents have objectives they value

  • Agents face constraints

  • Make tradeoffs to maximize objectives within constraints

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow